- Publication date
-
2022-05-09
- Topics
- Sharp, EL-506P, Manual
- Collection
- manuals_sharp; manuals; additional_collections
- Language
- English
Sharp EL-506P Manual — scan from original
- Addeddate
- 2022-05-09 14:46:19
- Identifier
- sharp-el-506-p-manual
- Identifier-ark
- ark:/13960/s2pf12prvn0
- Ocr
- tesseract 5.0.0-1-g862e
- Ocr_detected_lang
- en
- Ocr_detected_lang_conf
- 1.0000
- Ocr_detected_script
- Latin
- Ocr_detected_script_conf
- 0.7200
- Ocr_module_version
- 0.0.15
- Ocr_parameters
- -l eng
- Page_number_confidence
- 88.17
- Ppi
- 300
plus-circle Add Review
plus-circle Add Review
comment
Reviews
There are no reviews yet. Be the first one to
write a review.
Руководства Sharp EL506P Размер файлов: 5727 KB, Язык: English, Формат: pdf, Платформа: Windows/Linux, Дата: 2015-09-26
На данной странице вы можете скачать руководства Sharp EL506P. Мы предлагаем вам ознакомиться с руководством пользователя, инструкцией по сервисному обслуживанию и ремонту.
Также здесь вы найдете список заказных номеров на комплектующие Sharp EL506P.
Все файлы предоставляются исключительно в ознакомительных целях. И не являютя руководством по ремонту, а направлены лишь на то чтобы помочь вам более детально ознакомиться с принципом построения устройства.
Содержимое представленных здесь руководств требуют от вас знания технического английского языка.
Если вы собираетесь скачать руководство по сервисному обслуживанию Sharp EL506P, иными словами сервис мануал, вы дожны обладать хотя бы минимальными познаниями в области электроники и пониманием базовых принципов работы электромеханических устройств.
Для просмотра руководств вам понадобится Adobe Acrobat Reader версии 9 и выше либо другая программа для просмотра pdf файлов.
В связи с популярностью информации представленной на сайте и ее бесплатного предоставления конечному пользователю, убедительная просьба использовать специальные программные продукты для многопотокового скачивания файлов.
Руководства для Sharp EL506P
- Руководство пользователя (User manual)
- Руководство по сервисному обслуживанию (Service manual)
- Руководство по ремонту (Repair manual)
- Перечень комплектующих (PartList)
ENGLISH
INTRODUCTION
About operation examples, please refer to the attached sheet.
Refer to the number on the right of each title for use.
After reading this manual, store it in a convenient location for future
reference.
Note : One of the models described in this manual may not beavailable in some countries.
Operational NotesTo ensure trouble-free operation, please observe the following
points:
1. Do not carry the calculator in the back pocket of slacks ortrousers.
2. Do not subject the calculator to extreme temperatures.
3. Do not drop it or apply excessive force.
4. Clean only with a soft, dry cloth.
5. Do not use or store the calculator where fluids can splash onto it.
Press the RESET switch only in the following cases:
• When using for the first time
• After replacing the batteries
• To clear all memory contents
• When an abnormal condition occurs and all keys are inopera-
tive.
If service should be required on this calculator, use only a SHARP
servicing dealer, SHARP approved service facility, or SHARP re-
pair service where available.
Hard Case
EL-506V
EL-546V
SCIENTIFIC CALCULATOR
OPERATION MANUALMODEL
DISPLAY
Equation
Display Symbol
Mantissa Exponent
(During actual use not all symbols are displayed at the same time.)
/: Appears when the entire equation cannot be displayed.
Press to see the remaining (hidden) section.
xy /r
θ: Indicates the mode of expression of results in the com-
plex calculation mode.
2ndF : Appears when @ is pressed, indicating that the func-
tions shown in orange are enabled.
ALPHA : Indicates that @ K or O (R ) has been
pressed, and entry (recall) of memory contents and recall
of statistics can be performed.
FIX/SCI/ENG: Indicates the notation used to display a value and
changes each time @ f are pressed.
DEG/RAD/GRAD: Indicates angular units and changes each time
@b is pressed.
: Appears when a simulation calculation is executed.
STAT:Appears when statistics mode is selected.
M: Indicates that a numerical value is stored in the inde-
pendent memory.
?:Indicates that the calculator is waiting for a numerical
value to be entered, such as during simulation calcula-
tion.
:Appears when the calculator shows an angle as the
result in the complex calculation mode.
i :Indicates an imaginary number is being displayed in the
complex calculation mode.
ALGB
Multi-line Playback function (1)This calculator is equipped with a function to recall previous equa-
tions. Equations also include calculation ending instructions such
as “=” and a maximum of 142 characters can be stored in memory.
When the memory is full, stored equations are deleted in the order
of the oldest first. Pressing [ will display the previous equa-
tion. Further pressing [ will display preceding equations (after
returning to the previous equation, press ] to view equations
in order). In addition, @[ can be used to jump to the oldest
equation.
• The multi-line memory is cleared by the following operations:
@c , mode change, RESET, and N-base conversion.
For EL-546V, in addition to the above, pressing @f
(including the Automatic Power Off feature) will also clear the
multi-line memory.
Priority Levels in CalculationThis calculator performs operations according to the following pri-
ority:
1 ∠ 2 Functions preceded by their argument (x
-1, x2, n!, etc.) 3
Yx, x¿ 4 Implied multiplication of a memory value (2Y, etc.) 5
Functions followed by their argument (sin, cos, etc.) 6 Implied
multiplication of a function (2sin30, etc.) 7
nCr, nPr 8 × , ÷ 9 +, –
F AND G OR, XOR, XNOR H =, M+, M–, ⇒M, |DEG, |RAD,
| GRAD, DATA, CD, →rθ , → xy and other calculation ending in-
struction
• If parentheses are used, parenthesized calculations have prec- edence over any other calculations.
SCIENTIFIC CALCULATIONS
• Press @ m 0 to select the normal mode.
• In each example, press ª to clear the display. And if the FIX,
SCI, or ENG indicator is displayed, clear the indicator by press-
ing @ f .
Arithmetic Operations (2)• The closing parenthesis ) just before = or ; may be
omitted.
Constant Calculations (3)• In the constant calculations, the addend becomes a constant. Subtraction and division are performed in the same manner. For
multiplications, the multiplicand becomes a constant.
• When performing calculations using constants, constants will be displayed as K.
Functions (4)• Refer to operation examples of each function.
• Before starting calculations, specify the angular unit.
INITIAL SETUP
Mode Selection
Normal mode (NORMAL): @m0
Used to perform arithmetic operations and function calculations.
Complex number mode (CPLX): @m1
Used to perform arithmetic operations with complex numbers.
3-VLE mode (3-VLE): @m2
Used to perform simultaneous linear equations with three unknowns.
Statistic mode (STAT): @m3
Used to perform statistical calculations.
When executing mode selection, temporary memories, statistical
data and last answer memory will be cleared even when reselecting
the same mode.
Selecting the Display Notation and Decimal PlacesThe calculator has four display notation systems for displaying
calculation results. When FIX, SCI, or ENG symbol is displayed,
the number of decimal places can be set to any value between 0
and 9. Displayed values will be reduced to the corresponding
number of digits.
100000÷3=
[Floating point] ª100000 /3= 33333.33333
→ [FIXed decimal point] @f33333.33333
[TAB set to 2] @i 2 33333.33
→ [SCIentific notation] @f 3.33×10
4→ [ENGineering notation] @f 33.33×103→ [Floating point] @f33333.33333
• If the value for floating point system does not fit in the following
range, the calculator will display the result using scientific notation
system:
0.000000001 ≤ | x | ≤ 9999999999
Determination of the Angular UnitThis calculator has three angular units: DEG (°), RAD (Radians)
and GRAD (g).
Press @b to specify the angular unit.
1
3
y
x
b
xx
xx
a0
13 2
y
a b
x x
x
x x
1
0
2
3
f (x + –– )– f(x ––– )dx
2 d
x
2
f’ (x )= ————————
d x
[When performing integral calculations]
Integral calculations, depending on the
integrands and subintervals included, require
longer calculation time. During calculation,
“ Calculating! ” will be displayed. To cancel cal-
culation, press ª. In addition, please note
that there will be greater integral errors when
there are large fluctuations in the integral val-
ues during minute shifting of the integral range
and for periodic functions, etc., where positive
and negative integral values exist depending
on the interval.
For the former case, divide integral intervals
as small as possible. For the latter case,
separate the positive and negative values.
Following these tips will allow results of cal-
culations with greater accuracy and will also
shorten the calculation time.
Random NumbersA pseudo-random number with three significant digits can be gen-
erated by pressing @ ` = . To generate the next ran-
dom number, press =. You can perform this function in the
normal and statistics modes. (You cannot perform this function
while you are using the N-Base function.)
• Random numbers use memory Y. Each random number is gen-
erated on the basis of the value stored in memory Y (pseudo-
random number series).
Angular Unit Conversions (6)Each time @g are pressed, the angular unit changes in
sequence.
Memory Calculations (7)The calculator has six temporary memories (A-D, X and Y), one
independent memory (M) and one last answer memory (ANS). EL-
506V is also equipped with formula memories (F1 and F2) for
storing formulas.
Mode ANS M, F1, F2 A-D, X,Y
Normal
Complex ×
3-VLE ×××
Statistic ××
: Available× : Unavailable
[Temporary memories (A-D, X and Y)]
A stored value can be recalled as a value or variable for the use in
equations.
• In case you store an infinite decimal in the memory, recall it as a
variable to obtain accurate answers.
Ex.) 1 / 3 O Y (0.3333...is stored to Y)
3 * R Y =
0.999999999
3 * @ K Y =1.
[Independent memory (M)]
In addition to all the features of temporary memories, a value can
be added to or subtracted from an existing memory value.
[Last answer memory (ANS)]
The calculation result obtained by pressing = or any other
calculation ending instruction is automatically stored in the last
answer memory.
[Formula memories (F1 and F2)] : available only on EL-506V
Formulas up to 80 characters each can be stored. As with storing
numerical values in the memory, storing a new equation will auto-
matically replace any existing equation in memory without notifica-
tion.
Note:
Calculation results from the functions indicated below are auto-
matically stored in memories X or Y. For this reason, when using
these functions, be careful with the use of memories X and Y.
• Random numbers .................. Y memory
• →rθ , → xy ............................... X memory (r or x),
Y memory (θ or y)
Temporary memories and last answer memory are cleared even
when the same mode is reselected.
Chain Calculations (8)This calculator allows the previous calculation result to be used in
the following calculation.
The previous calculation result will not be recalled after entering
multiple instructions.
Fraction Calculations (9)This calculator performs arithmetic operations and memory calcu-
lations using a fraction, and conversion between a decimal number
and a fraction.
• In all cases, a total of up to 10 digits including integer, numera-
tor, denominator and the symbol ( l) can be entered.
• If the number of digits to be displayed is greater than 10, the
number is converted to and displayed as a decimal number.
• A decimal number, variable, or exponent cannot be used in a
fraction.
Binary, Octal, Decimal, and Hexadecimal Operations
(N-Base) (10)This calculator can perform conversions between numbers ex-
pressed in binary, octal, decimal and hexadecimal systems. It can
also perform the four basic arithmetic operations, calculations with
parentheses and memory calculations using binary, octal, decimal,
and hexadecimal numbers. In addition, the calculator can carry out
the logical operations AND, OR, NOT, NEG, XOR and XNOR on
binary, octal and hexadecimal numbers.
Conversion to each system is performed by the following keys:
@ê : Converts to the binary system. “
” appears.
@î : Converts to the octal system. “
” appears.
@ì : Converts to the hexadecimal system. “
” appears.
@í : Converts to the decimal system. “
”, “”, and “”
disappear from the display.
Conversion is performed on the displayed value when these keys
are pressed.
Note: In this calculator, the hexadecimal numbers A – F are entered
by pressing ë, Ñ , É , é , ç , and ∂,
and displayed as follows:
A → ï , B → ∫ , C → ó , D → ò , E → ô , F → ö
In the binary, octal, and hexadecimal systems, fractional parts
cannot be entered. When a decimal number having a fractional
part is converted into a binary, octal, or hexadecimal number, the
fractional part will be truncated. Likewise, when the result of a
binary, octal, or hexadecimal calculation includes a fractional part,
the fractional part will be truncated. In the binary, octal, and hexa-
decimal systems, negative numbers are displayed as a comple-
ment.
↔
Coordinate Conversions (12)• Before performing a calculation, select the angular unit.
Rectangular coord. Polar coord.
• Refer to the Note of the Memory Calculations section.
Calculations Using Physical Constants (13)See the quick reference card and the other side of the “Operation
Examples ” sheet.
A constant is recalled by pressing ß followed by the number of
the physical constant. You have to designate the physical constant
using 2-digit numbers. For example, speed of light in vacuum
should be designated as “01 ”.
The recalled constant appears in the display mode selected with
the designated number of decimal places.
Physical constants can be recalled in the normal mode (when not
set to binary, octal, or hexadecimal), 3-VLE mode, or statistics
mode.
Note: Physical constants and metric conversions are based either on the 1986 values released by the Committee on Data for
Science and Technology (CODATA) of ICSU (International
Council of Scientific Unions) or on ISO specifications.
Metric Conversions (14)See the quick reference card and the other side of the “Operation
Examples ” sheet.
Unit conversions can be performed in the normal (when not set to
binary, octal, or hexadecimal), 3-VLE and statistics modes.
Modify Function (15)In this calculator, all calculation results are internally obtained in
scientific notation with up to 12 digits for the mantissa. However,
since calculation results are displayed in the form designated by
the display notation and the number of decimal places indicated,
the internal calculation result may differ from that shown in the
display. By using the modify function, the internal value is con-
verted to match that of the display, so that the displayed value can
be used without change in subsequent operations.
SIMULATION CALCULATION (16)
If you have to find a value consecutively using the same formula,
such as plotting a curve line for 2 x2 + 1, or finding the variable for
2 x + 2 y =14, once you enter the equation, all you have to do is to
specify the value for the variable in the formula.
Usable variables: A-D, M, X and Y
Unusable functions: RANDOM
• Simulation calculations can only be executed in the normal mode.
• Calculation ending instructions (%, etc.) other than = cannot
be used.
Performing Calculations1 Press m0 .
2 Input a formula with at least one variable.
3 Press ≤.
4 Variable input screen will appear. Input the value of the flashing
variable, then press ® to confirm. The calculation result will
be displayed after entering the value for all used variables. • Only numerical values are allowed as variables. Input of for-
mulas are not permitted.
• Upon completing the calculation, press ≤ to perform cal-
culations using the same formula.
• Variables and numerical values stored in the memories will be
displayed in the variable input screen. To change a numerical
value, input the new value and press ®.
COMPLEX NUMBER CALCULATIONS (17)
To carry out addition, subtraction, multiplication, and division using
complex numbers, press @m1 to select the complex
number mode.
There are two modes of expression of the results of complex
number calculations.
1 Rectangular coordinate mode. ( xy appears on the display.)
∑2
2 Polar coordinate mode. (
rθ appears on the display.)
∑1
Complex number entry1 Rectangular coordinatesx-coordinate + y-coordinate Ü
or x-coordinate + Ü y-coordinate2Polar coordinatesr Ö θr: absolute value
θ: argument
• Upon changing to another mode, the imaginary portion of any
complex number stored in the independent memory (M) will be
cleared.
• A complex number expressed in rectangular coordinates with
the y-value equal to zero, or expressed in polar coordinates with
the angle equal to zero, is treated as a real number.
SIMULTANEOUS LINEAR EQUATIONS
WITH THREE UNKNOWNS (18)
To solve simultaneous linear equations with three unknowns, press
@m2 to select the 3-VLE mode.
Simultaneous Linear Equations with Three Unknowns:
Notes: •If the determinant D = 0, an error occurs.
• If the absolute value of an intermediate result or calcu-
lation result is 1 b× 10
100 or more, an error occurs.
Performing Calculations1 Press @m2 .
2 Enter each coefficient from a1 to d3 followed by ®, as
prompted on the display.
3 Upon pressing ® after entering d
3, the solution for x will be
displayed. Subsequent pressing will cycle through the values of
y , z and the determinant D.
• Coefficients can be entered using ordinary arithmetic operations.
• To clear the entered coefficients, press @c.
Note: Pressing ® when the determinant D is in the display
recalls the coefficients. Each time ® is pressed, a coeffi-
cient is displayed in the order of input, allowing the entered
coefficients to be verified. (by pressing @®, coeffi-
cients are displayed in reverse order.)
To correct a particular coefficient being displayed, enter the
correct value and then press ®.
If the coefficients c
1, c2 and c3 as well as a3 – d3 are set to zero, the
problem is treated as a 2-dimensional simultaneous equation. The
x and y values as well as the determinant can be retrieved.
a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3
a1 b1 c1a2 b2 c2a3 b3 c3 D =
STATISTICAL CALCULATIONS
Statistical calculations are performed in the statistics mode. Press
@m3 to select the statistics mode. This calculator per-
forms the seven statistical calculations indicated below. After se-
lecting the statistics mode, select the desired sub-mode by press-
ing the number key corresponding to your choice.
When changing to the statistical sub-mode, press the correspond-
ing number key after performing the operation to select the statis-
tics mode (press @m3).
0 (STAT 0) : Single-variable statistics
1 (STAT 1) : Linear regression calculation
2 (STAT 2) : Quadratic regression calculation
3 (STAT 3) : Exponential regression calculation
4 (STAT 4) : Logarithmic regression calculation
5 (STAT 5) : Power regression calculation
6 (STAT 6) : Inverse regression calculation
The following statistics can be obtained for each statistical calcula-
tion (refer to the table below):
Single-variable statistical calculation (19)Statistics of 1 and value of the normal probability function
Linear regression calculation (20)Statistics of 1 and 2 and, in addition, estimate of y for a given x
(estimate y´) and estimate of x for a given y (estimate x´)
Exponential regression, Logarithmic regression,Power regression, and Inverse regression calculationStatistics of 1 and 2. In addition, estimate of y for a given x and
estimate of x for a given y. (Since the calculator converts each
formula into a linear regression formula before actual calculation
takes place, it obtains all statistics, except coefficients a and b,
from converted data rather than entered data.)
Quadratic regression calculation (21)Statistics of 1 and 2 and coefficients a, b, c in the quadratic
regression formula ( y = a + bx + cx2). (For quadratic regression
calculations, no correlation coefficient ( r) can be obtained.) When
there are two x´ values, press @≠.
When performing calculations using a, b and c, only one numeric
value can be held.
N=2
n
h= b
– a
N
a ≤ x≤ b
Differential/Integral Functions (5)Differential and integral calculations are only available in the nor-
mal mode. For calculation conditions such as the x value in differ-
ential calculation or the initial point in integral calculation, only
numerical values can be entered and equations such as 2
2 cannot
be specified. It is possible to reuse the same equation over and
over again and to recalculate by only changing the conditions
without re-entering the equation.
• When performing a calculation, the value stored in the X memory
will be cleared.
• When performing a differential calculation, enter formula first
and then enter x value in differential calculation and minute
interval (d x). If a numerical value is not specified for minute
interval,
xf 0 will be x×10– 4 and x=0 will be 10–4 from the value of
the numeric derivative.
• When performing a integral calculation, enter formula first and
then enter a range of integral ( a, b) and subintervals (n). If a
numerical value is not specified for subintervals, calculation will
be performed using n=100.
Since differential and integral calculations are performed based on
the following equations, correct results may not be obtained, in
certain rare cases, when performing special calculations which
contain discontinuous points.
Integral calculation (Simpson ’s rule):
S= —h{ƒ (a )+4{ ƒ(a + h)+ ƒ(a +3 h)+ ······ +ƒ(a +(N –1) h)}
+2{ ƒ(a +2 h)+ ƒ(a +4 h)+ ······ +ƒ(a +(N –2) h)}+ f( b )}
Differential calculation:
Time, Decimal and Sexagesimal Calculations (11)Conversion between decimal and sexagesimal numbers can be
performed. In addition, the four basic arithmetic operations and
memory calculations can be carried out using the sexagesimal
system.
PRINTED IN CHINA / IMPRIM É EN CHINE
00LUP (TINSK0443EHZZ)
EL-506V/546V (K0443E)_ENGLISH_1
P ( x,y )
X
Y
0
y x
P (r,θ )
X
Y
0r
θ
1234567890.,
1234567890.,
1234567890.,
BEFORE USING THE CALCULATOR
Key Notation Used in this ManualIn this manual, key operations are described as follows: To specify
ex:@e
ln To specify E (HEX) : E
To specify ln :
I
To specify X : @KX
Functions that are printed in orange above the key require @ to
be pressed first before the key. Numbers are not shown as keys,
but as ordinary numbers.
Power On and OffPress ª to turn the calculator on, and @ f to turn it off.
Clearing MethodsThere are three clearing methods as follows:
Clearing Entry M A-D, X,Y
operation (Display) F1, F2 STAT, ANS*1
ª ××
@c ×
RESET
: Clear × : Retain
*1Statistical data and last answer memory.
Refer to the Memory Calculations section.
Editing the Equation• Press < or > to move the cursor. You can also return to
the equation after getting an answer by pressing > (< ).
See below for Multi-line playback function.
• If you need to delete a number, move the cursor to the number
you wish to delete then press d.
The number under the cursor will be deleted.
• If you need to insert a number, move the cursor to the place
immediately after where you wish to insert the number then enter
the number.
ex xE
x Mean of samples ( x data)sx Sample standard deviation ( x data)1σx Population standard deviation ( x data)n Number of samplesΣxSum of samples ( x data)Σx2Sum of squares of samples ( x data)
Entered data are kept in memory until @ c or @ m
3 are pressed. Before entering new data, clear the memory
contents.
[Data Entry]
Single-variable data
Data kData & frequency k (To enter multiples of the same
data)
Two-variable data
Data x & Data y kData x & Data y & frequency k (To enter multiples
of the same data x and y.)
[Data Correction]
Correction prior to pressing k:
Delete incorrect data with ª.
Correction after pressing k:
The inputted statistical data can be traced back by pressing
[ . Display the data to correct, press @J to delete,
then input the correct value.
Statistical Calculation Formulas (22)Refer also to the operation examples sheets.
In the statistical calculation formulas, an error will occur when:
• the absolute value of the intermediate result or calculation result
is equal to or greater than 1 × 10
100.
• the denominator is zero.
• an attempt is made to take the square root of a negative number.
• no solution exists in the quadratic regression calculation.
Normal Probability Calculations (19) (23)Refer also to the operation examples sheet.
•P(t), Q( t), and R( t) will always take positive values, even when
t ) automatically moves the cursor
back to the place in the equation where the error occurred. Edit the
equation or press ª to clear the equation.
Error Codes and Error Types
Syntax error (Error 1):•An attempt was made to perform an invalid operation.
Ex. 2 +- 5 =
Calculation error (Error 2):
• The absolute value of an intermediate or final calculation result equals
or exceeds 10
100.
• An attempt was made to divide by 0.
• The calculation ranges were exceeded while performing calculations.
Depth error (Error 3):
• The available number of buffers was exceeded. (There are 8 buffers*
for numeric values and 16 buffers for calculation instructions). *4
buffers in STAT and the complex number mode.
Equation too long (Error 4):
• The equation exceeded its maximum input buffer (142 characters).
An equation must be shorter than 142 characters.
Equation recall error (Error 5):
•The stored equation contains a function not available in the
mode used to recall the equation. For example, if a numerical
value with numbers other than 0 and 1 is stored as a decimal,
etc., it cannot be recalled when the calculator is set to binary.
Calculation Ranges (24)Refer also to the operation examples sheet.
•Within the ranges specified, this calculator is accurate to ±1 in
the least significant digit of the mantissa. When performing con-
tinuous calculations (including chain calculations), errors accu-
mulate leading to reduced accuracy.
• Calculation ranges
±10
-99 – ±9.999999999 ×1099 and 0.
If the absolute value of an entry or a final or intermediate result of a
calculation is less than 10
– 99, the value is considered to be 0 in
calculations and in the display.
BATTERY REPLACEMENT
Notes on Battery ReplacementImproper handling of batteries can cause electrolyte leakage or
explosion. Be sure to observe the following handling rules:
• Replace both batteries at the same time.
• Do not mix new and old batteries.
• Make sure the new batteries are the correct type.
• When installing, orient each battery properly as indicated in the
calculator.
When to Replace the BatteriesIf the display has poor contrast or nothing appears on the display
even when ª is pressed in dim lighting, it is time to replace the
batteries.
Caution• Keep batteries out of the reach of children.
• Exhausted batteries left in the calculator may leak and damage
the calculator.
• Explosion risk may be caused by incorrect handling.
• Batteries must be replaced only with others of the same type.
• Do not throw batteries into a fire as they may explode.
Replacement Procedure1. Turn the power off by pressing @ f .
2. Remove two screws. (Fig. 1)
3. Slide the battery cover slightly and lift it to remove.
4. Remove the used batteries by prying them with a ball-point pen or other similar pointed device. (Fig. 2)
5. Install two new batteries. Make sure the “+ ” side facing up.
6. Replace the cover and screws.
7. Press the RESET switch (on the back).
• Make sure that the display appears as shown below. If the
display does not appear as shown, remove the batteries reinstall
them and check the display once again.
(Fig. 1) (Fig. 2)
y Means of samples ( y data)sy Sample standard deviation ( y data)σy Population standard deviation ( y data)Σy Sum of samples ( y data)2Σy2Sum of squares of samples ( y data)Σxy Sum of products of samples ( x, y )r Correlation coefficienta Coefficient of regression equationbCoefficient of regression equation
c Coefficient of quadratic regression equation
1
x
Type Regression formulaLinear y = a + bxExponential y = a • ebx
Logarithmic y = a + b • ln xPower y = a • xb
Inverse y = a + b —
Quadratic y = a + bx + cx2
Automatic Power Off FunctionThis calculator will turn itself off to save battery power if no key is
pressed for approximately 10 minutes.
SPECIFICATIONS
Calculations: Scientific calculations, complex number
calculations, simultaneous linear
equations with three unknowns, statistical
calculations, etc.
Internal calculations: Mantissas of up to 12 digits
Pending operations: 16 calculations 8 numeric values
(4 numeric values in STAT and complex
number mode)
Power source: Built-in solar cells 3V ¶ (DC):
Backup batteries (Alkaline batteries (LR44)
× 2)
Operating temperature: 0 °C – 40 °C (32 °F – 104 °F)
External dimensions:78.6 mm (W) × 152 mm (D) × 10.5 mm (H)3-3/32 ” (W) × 5-31/32 ” (D) × 13/32 ” (H)
Weight: Approx. 78 g ( 0.172 lb)
(Including batteries)
Accessories: Batteries × 2 (installed), operation
manual, operation examples sheet, quick
reference card (Physical Constants and
Metric Conversions) and hard case
FOR MORE INFORMATION ABOUT THISCALCULATOR
Visit our Web site.
http://sharp-world.com/calculator/
1234567890.,
1234567890.,
1234567890.,
Расскажу, наверно о самом популярном калькуляторе в 1990-х годах — модели Sharp EL-506P.
Sharp EL-506P известен тем, что это самый подделываемый калькулятор ( http://mycalcdb.free.fr/main.php?l=0&id=1615 ). Я согласен с этим определением. В конце 1980-х — начале 1990-х годах появилось очень много копий этих машинок после того, как сделали клон микросхемы процессора.
Сам калькулятор относится к категории инженерных непрограммируемых калькуляторов. Его базовый набор функций очень продвинут и может решать наверно все задачи математики до высшей математики. Мне импонировало в нем наличие встроенных вычислений для 16-ричных чисел — я тогда активно осваивал программирование, в основном на ассемблере 6502, и частенько приходилось туда-сюда оперировать с десятичными и шестнадцатеричными числами. Тогда у меня был калькулятор «Электроника МК-71», и таких вычислений очень не хватало.
Калькуляторы с этим чипом до сих пор выпускаются под различными моделями. Например, из последних — Citizen SR-135N, Sharp EL-501XBWH
Что интересно, сама модель Sharp EL-506P выпускалась в двух вариантах. На фото ниже — два оригинальных варианта, с виду одинаковых, но отличающихся.
Условно можно назвать «вариант 1» и «вариант 2». Прежде всего обратите внимание, что кнопки у обоих машинок имеют своеобразные дефекты в середине. Не знаю, почему они возникли, но это такая особенность для этой модели.
Если вы обратили внимание, калькуляторы показывают разные числа. Это не просто так.
Когда-то, чтобы узнать точность вычислений, Mike Sebastian, решил на калькуляторах выполнять тест, вычислив для градусов формулу
arcsin (arccos (arctan (tan (cos (sin (9) ) ) ) ) )
Фишка в том, что точность разрядной сетки в калькуляторах ограничена, и при цепочечных вычислениях накапливается ошибка, которая становится значительной к концу вычислений.
Появился сайт http://www.rskey.org/~mwsebastian/miscprj/forensics.htm, где есть большой список калькуляторов, отсортированных как по моделям, так и по результату. Оказалось, что некоторые модели калькуляторов выдают один и тот же результат. Реально повторить один и тот же результат очень сложно — сказывается не только разрядная сетка, но и метод, по которому вычисляются функции. Одинаковый результат получается тогда, когда в разных моделях используется один и тот же чип или чип является потомком предыдущего. http://www.rskey.org/~mwsebastian/miscprj/results.htm
По этой таблице, кстати, можно легко определить, на базе каких моделей появились (или нет) те или иные копии, в том числе и для наших калькуляторов.
Для модели Sharp EL-506P встречается два разных результата. Это связано с тем, что модель выпускалась с двумя различными чипами. Почему это сделано, непонятно, но факт есть факт.
Недавно удалось раздобыть второй вариант калькулятора, и стало возможным написать эту статью, чтобы показать их отличия.
Сзади корпуса отличаются тем, что в первом варианте на корпусе есть бумажка с серийным номером, а во втором — нет. Винты в первом белого цвета, а во втором — черного.
Фирма Sharp в 1980-х годах практиковала безплатную (PCB-less) технологию сборки, когда нет ни печатных плат, ни паек. То есть каждый компонент вроде контактов батареи, солнечного элемента (если есть), пленка клавиатуры и чип процессора не паялись, а прижимались. Вот на этом сайте есть калькулятор в разобранном виде https://www.petervis.com/Calculators/Elsi%20Mate%20EL-860/Inside%20Elsi%20Mate%20EL-860.html.

Я очень удивился, когда в модели EL-515S увидел обычный электролитический конденсатор, одиноко лежащий в ячейке, а его ноги просто прижимались к пленке клавиатуры.
Всё это прижимается металлической пластиной. Без надобности лучше это не разбирать.
Это более крупно два разных чипа.
Дисплеи оригинальных калькуляторов радуют красотой сегментов, подложка индикатора очень светлая, и есть отличная контрастность.
Все же удалось найти отличия в сегментах между вариантом 1 и 2.
А вот две типичные подделки. Сразу бросается в глаза состояние клавиатуры на левом калькуляторе. В правом такого нет, но это на самом деле удача — найти калькулятор в таком состоянии. Я его сразу запихал в пленочный гриппер, чтобы ни коем образом не повредить краску. Она слезает при первой возможности. Наверно это связано с тем, что поддельщикам приходится дважды красить кнопки.
Можете прогуляться по нашим торговым площадкам и посмотреть, во что превращается клавиатура в подделках: https://meshok.net/?search=el-506p
Дисплеи в подделках тускловатые, и приходится искать угол, когда у них наибольшая белизна.
Можете сравнить шрифт на клавиатурах.
Самый простой способ определить подделку по фото — взглянуть на буквы a и b. В оригинале они красивые округлые, а в подделках — узкие и угловатые. Что интересно, на Ebay попадаются, в основном, оригиналы, а на наших площадках я оригиналов не видел ни разу.
Сзади в калькуляторах стоят обычные печатные платы с микросхемами-каплями.
Что интересно, кроме отличий в вычислениях между оригиналами вариантов 1 и 2, есть небольшие отличия в других вычислениях. Например, в варианте 1 и других моделях вроде EL-515S факториал 50! вычисляется с задержкой (умножает от 1 до 49), а в варианте 2 — там на числе 50 находится константа, и результат появляется сразу (с задержкой только до 49). Все подделки, что я видел, и современные выпуски основываются на варианте 2, и различий не найти.
Но в целом, если не брать в расчет качество сборки, дисплея и клавиатуры, калькуляторы вычисляют «на уровне», а набор функций делает калькулятор востребованным и сейчас.
UPD: Еще одну интересную особенность заметили. В том варианте EL-506P, с которого делали копии, линии сигналов индикатора совмещены с линиями опроса клавиатуры. Из-за чего если нажать одновременно [7] и [закрывающая скобка], то на дисплее на время нажатия испортится изображение из-за нарушения сигналов. В других версиях такого не наблюдается.

EL-506V
EL-546V
Operation Examples
Bedienungsbeispiele
Exemples d’opérations
Ejemplos de operación
Esempi di calcolo
Rekenvoorbeelden
Exemplos de Operação
Operationsexempel
Käyttöesimerkkejä
PRINTED IN CHINA/IMPRIMÉ EN CHINE/IMPRESO EN CHINA 00LUP(TINSZ0442EHZZ)
(1) []
|
1 |
3(5+2)= |
ª3 (5 +2 )= |
21. |
|||||
|
2 |
3× 5+2= |
3 *5 +2 = |
17. |
|||||
|
3 |
3× 5+3× 2= |
3 *5 +3 *2 = |
21. |
|||||
|
→ |
1 |
@[ |
||||||
|
→ |
2 |
] |
||||||
|
→ |
3 |
] |
||||||
|
→ |
2 |
[ |
||||||
|
(2) +-*/()±E |
||||||||
|
45+285÷3= |
ª45 |
+285 /3 = |
140. |
|||||
|
18+6 |
= |
(18 |
+6 )/ |
|||||
|
15–8 |
(15 |
-8 = |
3.428571429 |
|||||
|
42× |
(–5)+120= |
42 |
* |
5 ±+120 = |
–90. |
|||
|
*1 (±5) *1 |
||||||||
|
(5× 103)÷(4× 10–3)= 5 E3 /4 E3 ±= 1250000. |
||||||||
|
(3) |
||||||||
|
34+57= |
34 |
+ |
57 = |
91. |
||||
|
45+57= |
45 |
= |
102. |
|||||
|
68× |
25= |
68 |
* |
25 = |
1700. |
|||
|
68× |
40= |
40 = |
2720. |
|||||
(4) sutSUT°(sinh, sinh–1, cosh, cosh–1, tanh, tanh–1) VGIle ¡•L⁄™$#!q Q%
|
sin60[°]= |
ªs60 = |
0.866025403 |
|||||||
|
π |
@Gu(@V/ |
||||||||
|
cos–[rad]= |
|||||||||
|
4 |
4 )= |
0.707106781 |
|||||||
|
tan–11=[g] |
@G@T1 = |
50. |
|||||||
|
@G |
|||||||||
|
(cosh 1.5 + |
ª(°°°1*1 1.5 + |
||||||||
|
sinh 1.5)2 = |
|||||||||
|
°°11.5 )L=20.08553692 |
|||||||||
|
*1 cosh |
|||||||||
|
tanh–15– = |
°°°°2(5 / |
||||||||
|
7 |
7 )= |
0.895879734 |
|||||||
|
ln 20 = |
I20 = |
2.995732274 |
|||||||
|
log 50 = |
l50 = |
1.698970004 |
|||||||
|
e3 = |
@e3 = |
20.08553692 |
|||||||
|
101.7 = |
@¡1.7 = |
50.11872336 |
|||||||
|
1 |
1 |
6 @•+7 @•=0.309523809 |
|||||||
|
– + – = |
|||||||||
|
6 |
7 |
||||||||
|
8–2 – 34× 52 = |
8 ™2 ±-3 ™4 * |
||||||||
|
5 L= |
–2024.984375 |
||||||||
|
1 |
12 ™3 ™4 @•= 6.447419591 |
||||||||
|
– |
|||||||||
|
(123)4 = |
|||||||||
|
√ |
–4√ |
= |
@⁄49 -4 @$81 = 4. |
||||||
|
49 |
81 |
||||||||
|
3√ |
@#27 = |
3. |
|||||||
|
27= |
|||||||||
|
4! = |
4 @!= |
24. |
|||||||
|
10P3 = |
10 @q3 = |
720. |
|||||||
|
5C2 = |
5 @Q2 = |
10. |
|||||||
|
500× 25%= |
500 *25 @% |
125. |
|||||||
|
120÷400=?% |
120 /400 @% |
30. |
|||||||
|
500+(500× |
25%)= |
500 +25 @% |
625. |
||||||
|
400–(400× |
30%)= |
400 -30 @% |
280. |
||||||
|
θ |
= sin–1 x, θ |
= tan–1 x |
θ = cos–1 x |
||||||
|
DEG |
–90 ≤ |
θ |
≤ |
90 |
0 ≤ |
θ |
≤ |
180 |
|
|
RAD |
π |
θ |
≤ |
π |
0 ≤ |
θ |
≤ π |
||
|
– — ≤ |
— |
||||||||
|
2 |
2 |
||||||||
|
GRAD |
–100 ≤ |
θ |
≤ |
100 |
0 ≤ |
θ |
≤ |
200 |
|
(5) Åè
d/dx (x4 – 0.5x3 + 6x2) ª@KX™4 -0.5 @K
|
x=2 |
X™3 |
+6 @KXL |
||
|
dx=0.0002 |
@Å2 |
®® |
50. |
|
|
x=3 |
®3 ®0.001 ® |
130.500003 |
||
|
dx=0.001 |
||||
|
∫28 (x2 – 5)dx @KXL-5 |
||||
|
n=100 |
è2 ®8 ®® |
138. |
||
|
n=10 |
®®®10 ® |
138. |
||
(6) g
|
90°→ [rad] |
ª90 @g |
1.570796327 |
|
→ [g] |
@g |
100. |
|
→ [°] |
@g |
90. |
|
sin–10.8 = [°] |
@S0.8 = |
53.13010235 |
|
→ [rad] |
@g |
0.927295218 |
|
→ [g] |
@g |
59.03344706 |
|
→ [°] |
@g |
53.13010235 |
|
(7) RO;:?≥Ω |
|||||||||
|
F2 |
|||||||||
|
ª8 *2 OM |
16. |
||||||||
|
24÷(8× 2)= |
24 /RM= |
1.5 |
|||||||
|
(8× 2)× 5= |
RM*5 = |
80. |
|||||||
|
ªOM |
0. |
||||||||
|
$150× 3:M1 |
150 *3 ; |
450. |
|||||||
|
+)$250:M2 =M1+250 |
250 ; |
250. |
|||||||
|
–)M2× 5% |
RM*5 @% |
35. |
|||||||
|
M |
@:RM |
665. |
|||||||
|
$1= ¥140 |
140 OY |
140. |
|||||||
|
¥33,775=$? |
33775 /RY= |
241.25 |
|||||||
|
$2,750=¥? |
2750 *RY= |
385000. |
|||||||
|
[EL-506V] |
|||||||||
|
π r2 F1 |
@V@KY |
||||||||
|
LO≥ |
F1 |
||||||||
|
4 |
3 OY |
3. |
|||||||
|
3 |
|||||||||
|
V = ? |
R≥*4 /3 =37.69911184 |
||||||||
|
24 |
= 2.4…(A) |
24 /(4 +6 )= |
2.4 |
||||||
|
4+6 |
|||||||||
|
3 *@?+60 / |
|||||||||
|
3× (A)+60÷(A)= |
|||||||||
|
@?= |
32.2 |
||||||||
(8)
|
6+4=ANS |
ª6 |
+4 = |
10. |
||
|
ANS+5 |
+5 |
= |
15. |
||
|
44+37=ANS |
44 +37 = |
81. |
|||
|
√ |
= |
@⁄= |
9. |
||
|
ANS |
|||||
(9) |
|
1 4 |
b |
ª3 1 2 + |
|||
|
3– + – = [a–] |
|||||
|
2 3 |
c |
4 3 = |
4 l5 l6 * |
||
|
→ [a.xxx] |
4.833333333 |
||||
|
→ [d/c] |
@| |
29 l6 |
|||
|
2 |
|||||
|
10 |
3 |
= |
@¡2 3 = |
4.641588834 |
|
|
2 |
1.25 +2 5 = |
1.65 |
|||
|
1.25 + – = [a.xxx] |
|||||
|
b |
5 |
1 l13 l20 |
|||
|
→ [a–] |
|||||
|
c |
|||||
|
1.65 |
ª1.65 = |
1.65 |
|||
|
b |
1 l13 l20 |
||||
|
→ [a–] |
|||||
|
c |
|||||
|
→ [d/c] |
@| |
33 l20 |
|||
|
→ [a.xxx] |
1.65 |
5
* 4 l5 l6=4—
6
(10)комнгв†да
á
|
DEC(25)→ BIN |
ª@í25 @ê 11001.b |
||||
|
HEX(1AC) |
@ì1AC |
||||
|
→ |
BIN |
@ê |
110101100.b |
||
|
→ |
OCT |
@î |
654.0 |
||
|
→ |
DEC |
@í |
428. |
||
|
BIN |
@ê(1010 -100 ) |
||||
|
(1010–100)× 11 = *11 = |
10010.b |
||||
|
BIN(111)→ NEG ã111 = |
1111111001.b |
||||
|
HEX(1FF)+ |
@ì1FF @î+ |
||||
|
OCT(512)= |
512 = |
1511.0 |
|||
|
HEX(?) |
@ì |
349.H |
|||
|
2FEC– |
ªOM@ì2FEC — |
||||
|
2C9E=(A) |
2C9E ; |
34E.H |
|||
|
+)2000– |
2000 — |
||||
|
1901=(B) |
1901 ; |
6FF.H |
|||
|
(C) |
RM |
A4d.H |
|||
|
1011 AND |
ª@ê1011 † |
||||
|
101 = (BIN) |
101 = |
1.b |
|||
|
5A OR C3 = (HEX) @ì |
5A äC3 = |
db.H |
|||
|
NOT 10110 = |
@êâ10110 = |
1111101001.b |
|||
|
(BIN) |
|||||
|
24 XOR 4 = (OCT) @î |
24 à4 = |
20.0 |
|||
|
B3 XNOR |
@ìB3 á |
FFFFFFFF61.H |
|||
|
2D = (HEX) |
2D = |
||||
|
→ |
DEC |
@í |
–159. |
||
(11) o_
|
12°39’18”05 |
ª12 o39 o18 o5 |
|
|
→ [10] |
@_ |
12.65501389 |
|
123.678 |
123.678 @_ |
123°40’40.80 |
→[60]
|
3h30m45s + |
3 o30 o45 + |
|
|
6h45m36s = [60] |
6 o45 o36 = |
10°16’21.00 |
|
3h45m – 1.69h 3 o45 -1.69 = |
||
|
= [60] |
@_ |
2°03’36.00 |
sin62°12’24” = [10] s62 o12 o24 = 0.884635235
(12) °(→ rθ , → xy) ,≠
|
x = 6 |
r = |
ª6 @,4 °1[r ] 7.211102551 |
|||||
|
y = 4 |
→ |
θ = [°] |
@≠[θ ] |
33.69006753 |
|||
|
@≠[r ] |
7.211102551 |
||||||
|
r = 14 |
x = |
14 @,36 °2[x] |
11.32623792 |
||||
|
→ |
y = |
@≠[y] |
8.228993532 |
||||
|
θ = 36[°] |
@≠[x] |
11.32623792 |
|||||
(13) ß
|
V0 |
= 15.3m/s |
ª15.3 *10 +2 @•* |
|
|
t = 10s |
ß03 *10 L= 643.3325 |
||
|
1 |
2 |
||
|
V t+ – gt = ?m |
|||
|
0 |
2 |
(14) ¥
125yd = ?m ª125 @¥5 = 114.3
(15) j
|
5÷9=ANS |
ª@f@i1 |
|
|
ANS× 9= |
5 /9 = |
0.6 |
|
[FIX,TAB=1] |
*9 =*1 |
5.0 |
|
5 /9 =@j |
0.6 |
|
|
*9 =*2 |
5.4 |
|
|
@f@f@f |
*1 5.55555555555× 10–1× 9 *2 0.6× 9
(16) ≤®
@m0
f (x) = x3–3x2+2 @KX™3 -3 @K XL+2 ≤
|
x = –1 |
1 ±® |
–2. |
||
|
x = –0.5 |
≤0.5 ±® |
1.125 |
||
|
√ |
@⁄(@KAL |
|||
|
A2+B2 |
||||
|
+@KBL)≤ |
||||
|
A = 2, B = 3 |
2 ®3 ® |
3.605551275 |
||
|
A = 2, B = 5 |
≤®5 ® |
5.385164807 |
||
(17) m(CPLX)
@m1
(12–6i) + (7+15i) – 12 -6 Ü+7 +15 Ü-
|
(11+4i) = |
(11 +4 Ü)=[x] 8. |
|
|
@≠[y] |
+ 5.i |
|
|
@≠[x] |
8. |
|
|
6× (7–9i) × |
6 *(7 -9 Ü)* |
|
|
(–5+8i) = |
(5 ±+8 Ü)=[x] 222. |
|
|
@≠[y] |
+ 606.i |
|
|
16× (sin30°+ |
16 *(s30 +Üu30 ) |
|
|
icos30°)÷(sin60°+ |
/(s60 +Üu60 |
|
|
icos60°)= |
)=[x] |
13.85640646 |
|
@≠[y] |
+ 8. i |
|
y |
°18 Ö70 |
+12 Ö25 |
||||
|
A |
||||||
|
=[r] |
18.5408873 |
|||||
|
r1 |
r |
|||||
|
@≠[θ |
] |
42.76427608 |
||||
|
θ |
r2 |
B |
||||
|
θ 1 |
||||||
|
θ 2 |
x |
|||||
|
r1 = 8, θ 1 = 70° |
||||||
|
r2 = 12, θ 2 = 25° |
||||||
|
↓ |
||||||
|
r = ?, θ |
= ?° |
|
(1 + i) |
°21 +Ü= |
1. |
|
|
↓ |
°1[r] |
1.414213562 |
|
|
r = ?, θ = ?° |
@≠[θ ] |
45. |
|
|
°2(2 -3 Ü)L |
|||
|
(2 – 3i)2 = |
=[x] |
–5. |
|
|
@≠[y] |
– 12.i |
||
|
1 |
= |
(1 +Ü)@•=[x] 0.5 |
|
|
1 + i |
@≠[y] |
– 0.5i |
|
(18) m(3-VLE)
|
@m2 |
||||
|
x + y – z = 9 |
1 ®1 ®1 ±®9 ® |
|||
|
6x+6y – z =17 |
6 ®6 ®1 ±®17 ® |
|||
|
14x–7y+2z =42 |
14 ®7 ±®2 ®42 |
|||
|
x = ? |
®[x] |
3.238095238 |
||
|
y = ? |
®[y] |
–1.638095238 |
||
|
z = ? |
®[z] |
–7.4 |
||
|
det(D) = ? |
®[det(D)] |
105. |
||
|
2x + 3y = 4 |
@c2 ®3 ®®4 ® |
|||
|
5x + 6y = 7 |
||||
|
5 ®6 ®®7 ® |
||||
|
x = ? |
®®®®[x] |
–1. |
||
|
y = ? |
®[y] |
2. |
||
|
det(D) = ? |
®[det(D)] |
–3. |
||
(19) m(STAT0: SD) °(→ t, P(, Q(, R()
|
DATA |
0. |
||||||
|
95 |
@m30 |
||||||
|
80 |
95 k |
1. |
|||||
|
80 |
80 k |
2. |
|||||
|
75 |
k |
3. |
|||||
|
75 |
75 &3 k |
6. |
|||||
|
75 |
50 k |
7. |
|||||
|
50 |
|||||||
|
x= |
R~ |
75.71428571 |
|||||
|
σ |
x= |
Rp |
12.37179148 |
||||
|
Σ |
x= |
Rz |
530. |
||||
|
Σ x2 = |
Rw |
41200. |
|||||
|
sx= |
R£ |
13.3630621 |
|||||
|
sx2 = |
L= |
178.5714286 |
|||||
|
°°°°°2*1 60 ° |
|||||||
|
x = 60 → P(t) ? |
|||||||
|
°°°°1)= 0.102012 |
|||||||
|
t = –0.5 → R(t) ? °°°°°4 |
|||||||
|
0.5 ±)= |
0.691463 |
||||||
|
*1 P( |
|||||||
(20) m(STAT1: a+bx)
|
x |
y |
@m31 |
0. |
||
|
2 |
5 |
2 &5 k |
1. |
||
|
2 |
5 |
k |
2. |
||
|
12 |
24 |
12 |
&24 k |
3. |
|
|
21 |
40 |
21 |
&40 &3 k |
6. |
|
|
21 |
40 |
15 |
&25 k |
7. |
|
|
21 |
40 |
Ra |
1.050261097 |
||
|
15 |
25 |
Rb |
1.826044386 |
||
|
Rr |
0.995176343 |
||||
|
R£ |
8.541216597 |
||||
|
R¢ |
15.67223812 |
||||
|
x=3 → |
y’=? |
3 @y |
6.528394256 |
||
|
y=46 → |
x’=? |
46 |
@x |
24.61590706 |
|
(21) m(STAT2: ··+cx2)
|
x |
y |
@m32 |
0. |
||
|
12 |
41 |
12 |
&41 k |
1. |
|
|
8 |
13 |
8 &13 k |
2. |
||
|
5 |
2 |
5 &2 k |
3. |
||
|
23 |
200 |
23 |
&200 k |
4. |
|
|
15 |
71 |
15 |
&71 k |
5. |
|
|
Ra |
5.357506761 |
||||
|
Rb |
–3.120289663 |
||||
|
R© |
0.503334057 |
||||
|
x=10→ y’=? |
10 |
@y |
24.4880159 |
||
|
y=22→ |
x’=? |
22 |
@x |
9.63201409 |
|
|
@≠ |
–3.432772026 |
||||
|
@≠ |
9.63201409 |
||||
(22)
|
x = |
Σ x |
σ x = |
Σ x2 – nx2 |
|||||
|
n |
||||||||
|
n |
||||||||
|
Σ x = x1 + x2 + ··· +xn |
||||||||
|
sx = |
Σ x2 = x12 + x22 + ··· +xn2 |
|||||||
|
Σ y |
σ y = |
Σ y2 – ny2 |
||||||
|
= |
||||||||
|
y |
||||||||
|
n |
||||||||
|
n |
||||||||
|
Σ xy = x1y1 + x2y2 + ··· +xnyn |
||||||||||||||||
|
sy = |
Σ y = y1 + y2 + ··· +yn |
|||||||||||||||
|
Σ y2 = y12 + y22 + ··· +yn2 |
||||||||||||||||
|
(23) |
||||||||||||||||
x – x t = ––––σ x
(24)
|
Function |
Dynamic range |
|
Funktion |
zulässiger Bereich |
|
Fonction |
Plage dynamique |
|
Función |
Rango dinámico |
|
Funzioni |
Campi dinamici |
|
Functie |
Rekencapaciteit |
|
Função |
Limite dinâmico |
|
Funktion |
Definitionsområde |
|
Funktio |
Dynaaminen ala |
|
DEG: |
| x | < 1010 |
||||||||||||
|
(tan x : | x | ≠ |
90 (2n–1))* |
||||||||||||
|
sin x, cos x, |
RAD: |
π |
10 |
||||||||||
|
| x | < ––– |
× 10 |
π |
|||||||||||
|
tan x |
180 |
||||||||||||
|
(tan x : | x | ≠ |
– (2n–1))* |
||||||||||||
|
GRAD: |
10 |
10 |
2 |
||||||||||
|
| x | < —– |
× 10 |
||||||||||||
|
9 |
100 (2n–1))* |
||||||||||||
|
(tan x : | x | ≠ |
|||||||||||||
|
sin–1x, cos–1x |
| x | ≤ 1 |
||||||||||||
|
tan–1x, 3¿x |
| x | < 10100 |
||||||||||||
|
In x, log x |
10–99 ≤ |
x < 10100 |
|||||||||||
|
yx |
• |
y > 0: |
–10100 < x log y < 100 |
||||||||||
|
• |
y = 0: |
0 < x < 10100 |
1 |
||||||||||
|
• |
y < 0: |
||||||||||||
|
x = n (0 < | x | < 1: – = 2n–1, x ≠ 0)*, |
|||||||||||||
|
x |
|||||||||||||
|
–10100 < x log | y | < 100 |
|||||||||||||
|
• |
y > 0: |
100 |
1 |
||||||||||
|
–10 |
< – log y < 100 (x ≠ 0) |
||||||||||||
|
x¿y |
x |
||||||||||||
|
• |
y = 0: |
0 < x < 10100 |
|||||||||||
|
• |
y < 0: |
x = 2n–1 |
1 |
≠ 0)*, |
|||||||||
|
(0 < | x | < 1 : – = n, x |
|||||||||||||
|
1 |
x |
||||||||||||
|
100 |
|||||||||||||
|
–10 < – log | y | < 100 |
|||||||||||||
|
x |
|||||||||||||
|
ex |
–10100 < x ≤ 230.2585092 |
||||||||||||
|
10x |
–10100 < x < 100 |
||||||||||||
|
sinh x, cosh x, |
| x | ≤ 230.2585092 |
||||||||||||
|
tanh x |
|||||||||||||
|
sinh–1 x |
| x | < 1050 |
||||||||||||
|
cosh–1 x |
1 ≤ |
x < 1050 |
|||||||||||
|
tanh–1 x |
| x | < 1 |
||||||||||||
|
x2 |
| x | < 1050 |
||||||||||||
|
¿x |
0 ≤ |
x < 10100 |
|||||||||||
|
x–1 |
| x | < 10100 (x ≠ 0) |
||||||||||||
|
n! |
0 ≤ |
n ≤ |
69* |
||||||||||
|
nPr |
0 ≤ |
r ≤ |
n ≤ 9999999999* |
||||||||||
|
n! |
100 |
||||||||||||
|
–—– < 10 |
|||||||||||||
|
(n-r)! |
|||||||||||||
|
0 ≤ |
r ≤ |
n ≤ 9999999999* |
|||||||||||
|
nCr |
0 ≤ |
r ≤ |
69 |
||||||||||
|
n! |
100 |
||||||||||||
|
–—– < 10 |
|||||||||||||
|
(n-r)! |
|||||||||||||
|
↔ |
DEG, D°M’S |
0°00’00.01 ≤ | x | < 10000° |
|||||||||||
|
x, y → |
r, θ |
√ |
< 10100 |
||||||||||
|
x2 + y2 |
|||||||||||||
|
0 ≤ |
r < 10100 |
||||||||||||
|
r, θ → |
x, y |
DEG: |
| θ |
| < 1010 |
|||||||||
|
RAD: |
| θ |
π |
10 |
||||||||||
|
| < —–180 |
× 10 |
||||||||||||
|
GRAD : |
| θ |
10 |
10 |
||||||||||
|
| < –– × |
10 |
||||||||||||
|
9 |
|||||||||||||
|
DRG | |
DEG→ |
RAD, GRAD→ |
DEG: | x | < 10100 |
||||||||||
|
RAD→ |
GRAD: | x | < |
π– × 1098 |
|||||||||||
|
2 |
|||||||||||||
|
(A+Bi)+(C+Di) |
| A ± C | < 10100 |
||||||||||||
|
(A+Bi)–(C+Di) |
| B ± D | < 10100 |
||||||||||||
|
(A+Bi)× (C+Di) |
(AC – BD) < 10100 |
||||||||||||
|
(AD + BC) < 10100 |
|||||||||||||
|
AC + BD |
< 10100 |
||||||||||||
|
C2 + D2 |
|||||||||||||
|
(A+Bi)÷(C+Di) |
BC – AD |
< 10100 |
|||||||||||
|
C2 + D2 |
|||||||||||||
|
C2 + D2 ≠ |
0 |
||||||||||||
|
→ |
DEC |
DEC |
: |
| x | ≤ 9999999999 |
|||||||||
|
→ |
BIN |
BIN |
: |
1000000000 ≤ x ≤ |
1111111111 |
||||||||
|
→ |
OCT |
0 ≤ |
x ≤ |
111111111 |
|||||||||
|
→ |
HEX |
OCT |
: |
4000000000 ≤ x ≤ |
7777777777 |
||||||||
|
AND |
0 ≤ |
x ≤ |
3777777777 |
||||||||||
|
OR |
HEX |
: |
FDABF41C01 ≤ x ≤ FFFFFFFFFF |
||||||||||
|
XOR |
0 ≤ |
x ≤ |
2540BE3FF |
||||||||||
|
XNOR |
|||||||||||||
|
BIN |
: |
1000000000 ≤ x ≤ |
1111111111 |
||||||||||
|
0 ≤ |
x ≤ |
111111111 |
|||||||||||
|
NOT |
OCT |
: |
4000000000 ≤ x ≤ |
7777777777 |
|||||||||
|
0 ≤ |
x ≤ |
3777777777 |
|||||||||||
|
HEX |
: |
FDABF41C01 ≤ x ≤ FFFFFFFFFF |
|||||||||||
|
0 ≤ |
x ≤ |
2540BE3FE |
|||||||||||
|
BIN |
: |
1000000001 ≤ x ≤ |
1111111111 |
||||||||||
|
0 ≤ |
x ≤ |
111111111 |
|||||||||||
|
NEG |
OCT |
: |
4000000001 ≤ x ≤ |
7777777777 |
|||||||||
|
0 ≤ |
x ≤ |
3777777777 |
|||||||||||
|
HEX |
: |
FDABF41C01 ≤ x ≤ FFFFFFFFFF |
|||||||||||
|
0 ≤ |
x ≤ |
2540BE3FF |
* (n, r: integer / ganze Zahlen / entier / entero / intero / geheel getal / inteiros / heltal / kokonaisluku /  /
/  /
/ 

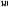
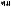 /
/ 

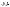
 /
/ 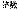 )
)
This equipment complies with the requirements of Directive 89/336/ EEC as amended by 93/68/EEC.
Dieses Gerät entspricht den Anforderungen der EG-Richtlinie 89/336/ EWG mit Änderung 93/68/EWG.
Ce matériel répond aux exigences contenues dans la directive 89/336/ CEE modifiée par la directive 93/68/CEE.
Dit apparaat voldoet aan de eisen van de richtlijn 89/336/EEG, gewijzigd door 93/68/EEG.
Dette udstyr overholder kravene i direktiv nr. 89/336/EEC med tillæg nr. 93/68/EEC.
Quest’ apparecchio è conforme ai requisiti della direttiva 89/336/EEC come emendata dalla direttiva 93/68/EEC.
89/336/ , !»! ! » #$ ! 93/68/ .
Este equipamento obedece às exigências da directiva 89/336/CEE na sua versão corrigida pela directiva 93/68/CEE.
Este aparato satisface las exigencias de la Directiva 89/336/CEE modificada por medio de la 93/68/CEE.
Denna utrustning uppfyller kraven enligt riktlinjen 89/336/EEC så som kompletteras av 93/68/EEC.
Dette produktet oppfyller betingelsene i direktivet 89/336/EEC i endringen 93/68/EEC.
Tämä laite täyttää direktiivin 89/336/EEC vaatimukset, jota on muutettu direktiivillä 93/68/EEC.
PHYSICAL CONSTANTS
ß01 — 40
|
No. SYMBOL |
UNIT |
No. SYMBOL |
UNIT |
No. SYMBOL UNIT |
||||||||||||
|
01 |
— c |
–1 |
15 |
— α |
29 |
— Vm |
3 |
–1 |
||||||||
|
m·s |
m ·mol |
|||||||||||||||
|
02 |
— G |
2 |
–2 |
16 |
— a0 |
m |
30 |
— R |
–1 |
–1 |
||||||
|
N·m·kg |
J·mol ·K |
|||||||||||||||
|
03 |
— g |
–2 |
17 |
— R∞ |
–1 |
31 |
— F |
–1 |
||||||||
|
m·s |
m |
C·mol |
||||||||||||||
|
04 |
— me |
kg |
18 |
— Φ |
0 |
Wb |
32 |
— RH |
Ω |
|||||||
|
05 |
— mp |
kg |
19 |
— µ |
Β |
–1 |
33 |
— e/me |
–1 |
|||||||
|
J·T |
C·kg |
|||||||||||||||
|
06 |
— mn |
kg |
20 |
— µ |
e |
–1 |
34 |
— h/2me |
–1 |
|||||||
|
J·T |
J·s·kg |
|||||||||||||||
|
07 |
— mµ |
kg |
21 |
— µ |
Ν |
–1 |
35 |
— γ p |
–1 |
–1 |
||||||
|
J·T |
s |
·T |
||||||||||||||
|
08 |
— u |
kg |
22 |
— µ |
P |
–1 |
36 |
— 2e/h |
–1 |
|||||||
|
J·T |
Hz·V |
|||||||||||||||
|
09 |
— e |
C |
23 |
— µ |
n |
–1 |
37 |
— eV |
J |
|||||||
|
J·T |
||||||||||||||||
|
10 |
— h |
J·s |
24 —µ |
µ |
–1 |
38 |
— t |
K |
||||||||
|
J·T |
||||||||||||||||
|
11 |
— k |
–1 |
25 |
— λ |
c |
m |
39 |
— AU |
m |
|||||||
|
J·K |
||||||||||||||||
|
12 |
— µ 0 |
–1 |
26 |
— λ |
cp |
m |
40 |
— pc |
m |
|||||||
|
H·m |
||||||||||||||||
|
13 |
— ε 0 |
–1 |
27 |
— σ |
–2 |
–4 |
||||||||||
|
F·m |
W·m ·K |
|||||||||||||||
|
14 |
— re |
m |
28 |
— Ν |
Α |
mol–1 |
||||||||||
|
METRIC CONVERSIONS |
x @¥1 — 44 |
|||||||||||||||
|
No. |
UNIT |
No. |
UNIT |
No. |
UNIT |
|||||||||||
|
1 |
in→ |
cm |
16 |
kg→ |
lb |
31 |
J→ calIT |
|||||||||
|
2 |
cm→ |
in |
17 |
°F→ |
°C |
32 |
calIT→ J |
|||||||||
|
3 |
ft→ m |
18 |
°C→ |
°F |
33 |
hp→ |
W |
|||||||||
|
4 |
m→ |
ft |
19 |
gal (US)→ l |
34 |
W→ |
hp |
|||||||||
|
5 |
yd→ |
m |
20 |
l→ |
gal (US) |
35 |
ps→ |
W |
||||||||
|
6 |
m→ |
yd |
21 |
gal (UK)→ l |
36 |
W→ |
ps |
|||||||||
|
7 |
mile→ km |
22 |
l→ |
gal (UK) |
37 |
kgf/cm2→ |
Pa |
|||||||||
|
8 |
km→ |
mile |
23 |
fl oz (US)→ |
ml |
38 |
Pa→ |
kgf/cm2 |
||||||||
|
9 |
n mile→ |
m |
24 |
ml→ |
fl oz (US) |
39 |
atm→ |
Pa |
||||||||
|
10 |
m→ |
n mile |
25 |
fl oz (UK)→ |
ml |
40 |
Pa→ |
atm |
||||||||
|
11 |
acre→ |
m2 |
26 |
ml→ |
fl oz (UK) |
41 |
mmHg→ Pa |
|||||||||
|
12 |
m2→ |
acre |
27 |
J→ |
cal |
42 |
Pa→ |
mmHg |
||||||||
|
13 |
oz→ |
g |
28 |
cal→ |
J |
43 |
kgf·m→ J |
|||||||||
|
14 |
g→ oz |
29 |
J→ |
cal15 |
44 |
J→ kgf·m |
||||||||||
|
15 |
lb→ |
kg |
30 |
cal15→ |
J |
|||||||||||
 Loading…
Loading…
You can only view or download manuals with
Sign Up and get 5 for free
Upload your files to the site. You get 1 for each file you add
Get 1 for every time someone downloads your manual
Buy as many as you need
ENGLISH
SCIENTIFIC CALCULATOR
EL-506V
EL-546V
MODEL
OPERATION MANUAL
PRINTED IN CHINA / IMPRIMÉ EN CHINE
00LUP (TINSK0443EHZZ)
INTRODUCTION
About operation examples, please refer to the attached sheet.
Refer to the number on the right of each title for use.
After reading this manual, store it in a convenient location for future
reference.
Note : One of the models described in this manual may not be
available in some countries.
Operational Notes
To ensure trouble-free operation, please observe the following
points:
1. Do not carry the calculator in the back pocket of slacks or
trousers.
2. Do not subject the calculator to extreme temperatures.
3. Do not drop it or apply excessive force.
4. Clean only with a soft, dry cloth.
5. Do not use or store the calculator where fluids can splash onto it.
Press the RESET switch only in the following cases:
• When using for the first time
• After replacing the batteries
• To clear all memory contents
• When an abnormal condition occurs and all keys are inopera-
tive.
If service should be required on this calculator, use only a SHARP
servicing dealer, SHARP approved service facility, or SHARP re-
pair service where available.
Hard Case
DISPLAY
Equation
Display
Mantissa
Exponent
(During actual use not all symbols are displayed at the same time.)
: Appears when the entire equation cannot be displayed.
/
Press
/
to see the remaining (hidden) section.
xy/r
: Indicates the mode of expression of results in the com-
plex calculation mode.
2ndF
: Appears when
is pressed, indicating that the func-
tions shown in orange are enabled.
ALPHA : Indicates that
or
(
) has been
pressed, and entry (recall) of memory contents and recall
of statistics can be performed.
FIX/SCI/ENG: Indicates the notation used to display a value and
changes each time
are pressed.
DEG/RAD/GRAD: Indicates angular units and changes each time
is pressed.
ALGB
: Appears when a simulation calculation is executed.
: Appears when statistics mode is selected.
STAT
M
: Indicates that a numerical value is stored in the inde-
pendent memory.
?
: Indicates that the calculator is waiting for a numerical
value to be entered, such as during simulation calcula-
tion.
: Appears when the calculator shows an angle as the
result in the complex calculation mode.
i
: Indicates an imaginary number is being displayed in the
complex calculation mode.
BEFORE USING THE CALCULATOR
Key Notation Used in this Manual
In this manual, key operations are described as follows:
e
x
To specify
:
e
x
x
E
To specify E (HEX) : E
ln
To specify ln
:
To specify X
:
Functions that are printed in orange above the key require
be pressed first before the key. Numbers are not shown as keys,
but as ordinary numbers.
Power On and Off
Press
to turn the calculator on, and
to turn it off.
Clearing Methods
There are three clearing methods as follows:
Clearing
Entry
M
operation
(Display)
F1, F2
STAT, ANS*
RESET
: Clear
: Retain
1
*
Statistical data and last answer memory.
Refer to the Memory Calculations section.
Editing the Equation
• Press
or
to move the cursor. You can also return to
the equation after getting an answer by pressing
See below for Multi-line playback function.
• If you need to delete a number, move the cursor to the number
you wish to delete then press
.
The number under the cursor will be deleted.
• If you need to insert a number, move the cursor to the place
immediately after where you wish to insert the number then enter
the number.
Multi-line Playback function
This calculator is equipped with a function to recall previous equa-
tions. Equations also include calculation ending instructions such
as «=» and a maximum of 142 characters can be stored in memory.
When the memory is full, stored equations are deleted in the order
of the oldest first. Pressing
will display the previous equa-
tion. Further pressing
will display preceding equations (after
returning to the previous equation, press
to view equations
in order). In addition,
can be used to jump to the oldest
equation.
• The multi-line memory is cleared by the following operations:
, mode change, RESET, and N-base conversion.
For EL-546V, in addition to the above, pressing
(including the Automatic Power Off feature) will also clear the
multi-line memory.
Priority Levels in Calculation
This calculator performs operations according to the following pri-
1 2
ority:
4
Functions preceded by their argument (x
-1
, x
2
, n!, etc.)
Y
x
,
x
Implied multiplication of a memory value (2Y, etc.)
7
8
Functions followed by their argument (sin, cos, etc.)
F
G
H
multiplication of a function (2sin30, etc.)
C
,
P
n
r
n
r
M, |DEG, |RAD,
AND
OR, XOR, XNOR
=, M+, M–,
|GRAD, DATA, CD,
r ,
xy and other calculation ending in-
struction
• If parentheses are used, parenthesized calculations have prec-
edence over any other calculations.
INITIAL SETUP
Mode Selection
Normal mode (NORMAL):
Used to perform arithmetic operations and function calculations.
Complex number mode (CPLX):
Used to perform arithmetic operations with complex numbers.
3-VLE mode (3-VLE):
Used to perform simultaneous linear equations with three unknowns.
Statistic mode (STAT):
Used to perform statistical calculations.
When executing mode selection, temporary memories, statistical
data and last answer memory will be cleared even when reselecting
the same mode.
Selecting the Display Notation and Decimal Places
The calculator has four display notation systems for displaying
calculation results. When FIX, SCI, or ENG symbol is displayed,
the number of decimal places can be set to any value between 0
and 9. Displayed values will be reduced to the corresponding
number of digits.
100000÷3=
[Floating point]
100000
3
33333.33333
[FIXed decimal point]
33333.33333
[TAB set to 2]
2
33333.33
[SCIentific notation]
[ENGineering notation]
[Floating point]
33333.33333
• If the value for floating point system does not fit in the following
range, the calculator will display the result using scientific notation
system:
0.000000001
| x |
9999999999
Determination of the Angular Unit
This calculator has three angular units: DEG (°), RAD (Radians)
and GRAD (g).
Press
to specify the angular unit.
SCIENTIFIC CALCULATIONS
• Press
to select the normal mode.
• In each example, press
to clear the display. And if the FIX,
SCI, or ENG indicator is displayed, clear the indicator by press-
ing
.
Arithmetic Operations
• The closing parenthesis
just before
omitted.
Constant Calculations
• In the constant calculations, the addend becomes a constant.
Subtraction and division are performed in the same manner. For
multiplications, the multiplicand becomes a constant.
• When performing calculations using constants, constants will be
displayed as K.
Functions
• Refer to operation examples of each function.
• Before starting calculations, specify the angular unit.
Differential/Integral Functions
Differential and integral calculations are only available in the nor-
mal mode. For calculation conditions such as the x value in differ-
ential calculation or the initial point in integral calculation, only
numerical values can be entered and equations such as 2
be specified. It is possible to reuse the same equation over and
over again and to recalculate by only changing the conditions
without re-entering the equation.
• When performing a calculation, the value stored in the X memory
will be cleared.
• When performing a differential calculation, enter formula first
and then enter x value in differential calculation and minute
interval (dx). If a numerical value is not specified for minute
x
x
x
interval,
0 will be
10
–4
and
=0 will be 10
the numeric derivative.
• When performing a integral calculation, enter formula first and
then enter a range of integral (a, b) and subintervals (n). If a
numerical value is not specified for subintervals, calculation will
be performed using n=100.
Since differential and integral calculations are performed based on
the following equations, correct results may not be obtained, in
certain rare cases, when performing special calculations which
contain discontinuous points.
Symbol
Integral calculation (Simpson’s rule):
1
S=—h{ (a)+4{ (a+h)+ (a+3h)+······+ (a+(N–1)h)}
3
+2{ (a+2h)+ (a+4h)+······+ (a+(N–2)h)}+f(b)}
Differential calculation:
dx
f(x+ ––)–f(x– ––)
2
f'(x)=————————
dx
[When performing integral calculations]
Integral calculations, depending on the
integrands and subintervals included, require
longer calculation time. During calculation,
«Calculating!» will be displayed. To cancel cal-
culation, press
. In addition, please note
that there will be greater integral errors when
there are large fluctuations in the integral val-
ues during minute shifting of the integral range
and for periodic functions, etc., where positive
and negative integral values exist depending
on the interval.
For the former case, divide integral intervals
as small as possible. For the latter case,
separate the positive and negative values.
Following these tips will allow results of cal-
culations with greater accuracy and will also
shorten the calculation time.
Random Numbers
A pseudo-random number with three significant digits can be gen-
erated by pressing
dom number, press
. You can perform this function in the
normal and statistics modes. (You cannot perform this function
while you are using the N-Base function.)
• Random numbers use memory Y. Each random number is gen-
erated on the basis of the value stored in memory Y (pseudo-
random number series).
Angular Unit Conversions
Each time
are pressed, the angular unit changes in
sequence.
Memory Calculations
The calculator has six temporary memories (A-D, X and Y), one
independent memory (M) and one last answer memory (ANS). EL-
506V is also equipped with formula memories (F1 and F2) for
to
storing formulas.
Mode
ANS
Normal
Complex
3-VLE
Statistic
A-D, X,Y
1
: Available
: Unavailable
[Temporary memories (A-D, X and Y)]
A stored value can be recalled as a value or variable for the use in
equations.
• In case you store an infinite decimal in the memory, recall it as a
variable to obtain accurate answers.
Ex.) 1
3
3
3
[Independent memory (M)]
(
).
In addition to all the features of temporary memories, a value can
be added to or subtracted from an existing memory value.
[Last answer memory (ANS)]
The calculation result obtained by pressing
calculation ending instruction is automatically stored in the last
answer memory.
[Formula memories (F1 and F2)] : available only on EL-506V
Formulas up to 80 characters each can be stored. As with storing
(1)
numerical values in the memory, storing a new equation will auto-
matically replace any existing equation in memory without notifica-
tion.
Note:
Calculation results from the functions indicated below are auto-
matically stored in memories X or Y. For this reason, when using
these functions, be careful with the use of memories X and Y.
•
Random numbers ……………… Y memory
•
r ,
xy …………………………. X memory (r or x),
Y memory ( or y)
Temporary memories and last answer memory are cleared even
when the same mode is reselected.
Chain Calculations
This calculator allows the previous calculation result to be used in
the following calculation.
The previous calculation result will not be recalled after entering
3
multiple instructions.
5
6
Fraction Calculations
9
Implied
This calculator performs arithmetic operations and memory calcu-
, ÷
+, –
lations using a fraction, and conversion between a decimal number
and a fraction.
• In all cases, a total of up to 10 digits including integer, numera-
tor, denominator and the symbol (l) can be entered.
• If the number of digits to be displayed is greater than 10, the
number is converted to and displayed as a decimal number.
• A decimal number, variable, or exponent cannot be used in a
fraction.
Binary, Octal, Decimal, and Hexadecimal Operations
(N-Base)
This calculator can perform conversions between numbers ex-
pressed in binary, octal, decimal and hexadecimal systems. It can
also perform the four basic arithmetic operations, calculations with
parentheses and memory calculations using binary, octal, decimal,
and hexadecimal numbers. In addition, the calculator can carry out
the logical operations AND, OR, NOT, NEG, XOR and XNOR on
binary, octal and hexadecimal numbers.
Conversion to each system is performed by the following keys:
: Converts to the binary system. » » appears.
: Converts to the octal system. » » appears.
: Converts to the hexadecimal system. » » appears.
: Converts to the decimal system. » «, » «, and » «
disappear from the display.
Conversion is performed on the displayed value when these keys
are pressed.
Note: In this calculator, the hexadecimal numbers A – F are entered
by pressing
,
,
and displayed as follows:
A
, B
, C
, D
, E
In the binary, octal, and hexadecimal systems, fractional parts
cannot be entered. When a decimal number having a fractional
3.33 10
4
part is converted into a binary, octal, or hexadecimal number, the
33.33 10
3
fractional part will be truncated. Likewise, when the result of a
binary, octal, or hexadecimal calculation includes a fractional part,
the fractional part will be truncated. In the binary, octal, and hexa-
decimal systems, negative numbers are displayed as a comple-
ment.
Time, Decimal and Sexagesimal Calculations
Conversion between decimal and sexagesimal numbers can be
performed. In addition, the four basic arithmetic operations and
memory calculations can be carried out using the sexagesimal
system.
Coordinate Conversions
• Before performing a calculation, select the angular unit.
Y
y
0
Rectangular coord.
(2)
or
may be
• Refer to the Note of the Memory Calculations section.
Calculations Using Physical Constants
(3)
See the quick reference card and the other side of the «Operation
Examples» sheet.
A constant is recalled by pressing
the physical constant. You have to designate the physical constant
using 2-digit numbers. For example, speed of light in vacuum
should be designated as «01».
The recalled constant appears in the display mode selected with
(4)
the designated number of decimal places.
Physical constants can be recalled in the normal mode (when not
set to binary, octal, or hexadecimal), 3-VLE mode, or statistics
(5)
mode.
Note: Physical constants and metric conversions are based either
on the 1986 values released by the Committee on Data for
Science and Technology (CODATA) of ICSU (International
2
cannot
Council of Scientific Unions) or on ISO specifications.
Metric Conversions
See the quick reference card and the other side of the «Operation
Examples» sheet.
Unit conversions can be performed in the normal (when not set to
binary, octal, or hexadecimal), 3-VLE and statistics modes.
Modify Function
–4
from the value of
In this calculator, all calculation results are internally obtained in
scientific notation with up to 12 digits for the mantissa. However,
since calculation results are displayed in the form designated by
the display notation and the number of decimal places indicated,
the internal calculation result may differ from that shown in the
display. By using the modify function, the internal value is con-
verted to match that of the display, so that the displayed value can
be used without change in subsequent operations.
SIMULATION CALCULATION
b – a
If you have to find a value consecutively using the same formula,
h=
N
such as plotting a curve line for 2x
N=2n
2x + 2y =14, once you enter the equation, all you have to do is to
a x b
specify the value for the variable in the formula.
Usable variables: A-D, M, X and Y
Unusable functions: RANDOM
dx
• Simulation calculations can only be executed in the normal mode.
2
• Calculation ending instructions (%, etc.) other than
be used.
Performing Calculations
1
2
Press
.
3
Input a formula with at least one variable.
4
Press
.
y
Variable input screen will appear. Input the value of the flashing
variable, then press
be displayed after entering the value for all used variables.
• Only numerical values are allowed as variables. Input of for-
mulas are not permitted.
x
a
b
x x
0
1
• Upon completing the calculation, press
x
2
x
3
culations using the same formula.
y
• Variables and numerical values stored in the memories will be
x
x
0
2
displayed in the variable input screen. To change a numerical
b
a
x
value, input the new value and press
x
x
1
3
COMPLEX NUMBER CALCULATIONS
To carry out addition, subtraction, multiplication, and division using
complex numbers, press
number mode.
. To generate the next ran-
There are two modes of expression of the results of complex
1
number calculations.
Rectangular coordinate mode. (xy appears on the display.)
2
Polar coordinate mode. ( r appears on the display.)
Complex number entry
1
(6)
Rectangular coordinates
x-coordinate
2
or x-coordinate
Polar coordinates
(7)
r
r: absolute value
: argument
• Upon changing to another mode, the imaginary portion of any
complex number stored in the independent memory (M) will be
cleared.
M, F1, F2
A-D, X,Y
• A complex number expressed in rectangular coordinates with
the y-value equal to zero, or expressed in polar coordinates with
the angle equal to zero, is treated as a real number.
SIMULTANEOUS LINEAR EQUATIONS
WITH THREE UNKNOWNS
To solve simultaneous linear equations with three unknowns, press
to select the 3-VLE mode.
Simultaneous Linear Equations with Three Unknowns:
a
x + b
y + c
z = d
1
1
1
a
x + b
y + c
z = d
2
2
2
x + b
y + c
z = d
a
3
3
3
(0.3333…is stored to Y)
0.999999999
Notes:
• If the determinant D = 0, an error occurs.
1.
• If the absolute value of an intermediate result or calcu-
lation result is 1
Performing Calculations
1
2
Press
Enter each coefficient from a
3
prompted on the display.
or any other
Upon pressing
displayed. Subsequent pressing will cycle through the values of
y, z and the determinant D.
• Coefficients can be entered using ordinary arithmetic operations.
• To clear the entered coefficients, press
Note: Pressing
recalls the coefficients. Each time
cient is displayed in the order of input, allowing the entered
coefficients to be verified. (by pressing
cients are displayed in reverse order.)
To correct a particular coefficient being displayed, enter the
correct value and then press
If the coefficients c
, c
1
problem is treated as a 2-dimensional simultaneous equation. The
x and y values as well as the determinant can be retrieved.
(8)
STATISTICAL CALCULATIONS
Statistical calculations are performed in the statistics mode. Press
to select the statistics mode. This calculator per-
forms the seven statistical calculations indicated below. After se-
lecting the statistics mode, select the desired sub-mode by press-
(9)
ing the number key corresponding to your choice.
When changing to the statistical sub-mode, press the correspond-
ing number key after performing the operation to select the statis-
tics mode (press
(STAT 0) : Single-variable statistics
(STAT 1) : Linear regression calculation
(STAT 2) : Quadratic regression calculation
(STAT 3) : Exponential regression calculation
(STAT 4) : Logarithmic regression calculation
(STAT 5) : Power regression calculation
(10)
(STAT 6) : Inverse regression calculation
The following statistics can be obtained for each statistical calcula-
tion (refer to the table below):
Single-variable statistical calculation
1
Statistics of
and value of the normal probability function
Linear regression calculation
1
Statistics of
and
(estimate y´) and estimate of x for a given y (estimate x´)
Exponential regression, Logarithmic regression,
Power regression, and Inverse regression calculation
1
Statistics of
and
estimate of x for a given y. (Since the calculator converts each
formula into a linear regression formula before actual calculation
takes place, it obtains all statistics, except coefficients a and b,
from converted data rather than entered data.)
Quadratic regression calculation
1
Statistics of
and
,
,
, and
,
regression formula (y = a + bx + cx
calculations, no correlation coefficient (r) can be obtained.) When
there are two x´ values, press
, F
When performing calculations using a, b and c, only one numeric
value can be held.
Mean of samples (x data)
x
1
sx
Sample standard deviation (x data)
Population standard deviation (x data)
x
n
Number of samples
x
Sum of samples (x data)
2
x
Sum of squares of samples (x data)
(11)
2
(12)
Y
P (x,y )
P (r, )
r
X
X
0
x
Entered data are kept in memory until
Polar coord.
contents.
[Data Entry]
(13)
Single-variable data
Data
Data
followed by the number of
data)
Two-variable data
Data x
Data x
of the same data x and y.)
[Data Correction]
Correction prior to pressing
Delete incorrect data with
Correction after pressing
The inputted statistical data can be traced back by pressing
then input the correct value.
Statistical Calculation Formulas
Refer also to the operation examples sheets.
(14)
Linear
Exponential
Logarithmic
Power
(15)
Inverse
Quadratic
In the statistical calculation formulas, an error will occur when:
• the absolute value of the intermediate result or calculation result
is equal to or greater than 1
• the denominator is zero.
• an attempt is made to take the square root of a negative number.
• no solution exists in the quadratic regression calculation.
(16)
Normal Probability Calculations
Refer also to the operation examples sheet.
2
+ 1, or finding the variable for
• P(t), Q(t), and R(t) will always take positive values, even when
t<0, because these functions follow the same principle used
when solving for an area.
Values for P(t), Q(t), and R(t) are given to six decimal places.
cannot
ERROR AND CALCULATION RANGES
Errors
An error will occur if an operation exceeds the calculation ranges,
or if a mathematically illegal operation is attempted. When an error
occurs, pressing
back to the place in the equation where the error occurred. Edit the
equation or press
to confirm. The calculation result will
Error Codes and Error Types
Syntax error (Error 1):
to perform cal-
• An attempt was made to perform an invalid operation.
Calculation error (Error 2):
.
• The absolute value of an intermediate or final calculation result equals
or exceeds 10
• An attempt was made to divide by 0.
• The calculation ranges were exceeded while performing calculations.
(17)
Depth error (Error 3):
• The available number of buffers was exceeded. (There are 8 buffers*
for numeric values and 16 buffers for calculation instructions). *4
to select the complex
buffers in STAT and the complex number mode.
Equation too long (Error 4):
• The equation exceeded its maximum input buffer (142 characters).
An equation must be shorter than 142 characters.
Equation recall error (Error 5):
• The stored equation contains a function not available in the
mode used to recall the equation. For example, if a numerical
value with numbers other than 0 and 1 is stored as a decimal,
etc., it cannot be recalled when the calculator is set to binary.
y-coordinate
y-coordinate
Calculation Ranges
Refer also to the operation examples sheet.
• Within the ranges specified, this calculator is accurate to ±1 in
the least significant digit of the mantissa. When performing con-
tinuous calculations (including chain calculations), errors accu-
mulate leading to reduced accuracy.
• Calculation ranges
If the absolute value of an entry or a final or intermediate result of a
calculation is less than 10
calculations and in the display.
BATTERY REPLACEMENT
(18)
Notes on Battery Replacement
Improper handling of batteries can cause electrolyte leakage or
explosion. Be sure to observe the following handling rules:
• Replace both batteries at the same time.
• Do not mix new and old batteries.
a
b
c
1
1
1
1
• Make sure the new batteries are the correct type.
a
b
c
D =
2
2
2
2
• When installing, orient each battery properly as indicated in the
a
b
c
3
3
3
3
calculator.
When to Replace the Batteries
If the display has poor contrast or nothing appears on the display
even when
10
100
or more, an error occurs.
batteries.
Caution
.
• Keep batteries out of the reach of children.
to d
followed by
,
as
1
3
• Exhausted batteries left in the calculator may leak and damage
the calculator.
after entering d
, the solution for x will be
3
• Explosion risk may be caused by incorrect handling.
• Batteries must be replaced only with others of the same type.
• Do not throw batteries into a fire as they may explode.
.
Replacement Procedure
when the determinant D is in the display
1. Turn the power off by pressing
is pressed, a coeffi-
2. Remove two screws. (Fig. 1)
3. Slide the battery cover slightly and lift it to remove.
, coeffi-
4. Remove the used batteries by prying them with a ball-point pen
or other similar pointed device. (Fig. 2)
5. Install two new batteries. Make sure the «+» side facing up.
.
6. Replace the cover and screws.
7. Press the RESET switch (on the back).
and c
as well as a
– d
are set to zero, the
2
3
3
3
• Make sure that the display appears as shown below. If the
display does not appear as shown, remove the batteries reinstall
them and check the display once again.
).
Automatic Power Off Function
This calculator will turn itself off to save battery power if no key is
pressed for approximately 10 minutes.
SPECIFICATIONS
Calculations:
Internal calculations:
(19)
Pending operations:
(20)
2
Power source:
and, in addition, estimate of y for a given x
2
Operating temperature: 0°C – 40°C (32°F – 104°F)
External dimensions:
. In addition, estimate of y for a given x and
Weight:
Accessories:
(21)
2
and coefficients a, b, c in the quadratic
2
). (For quadratic regression
.
FOR MORE INFORMATION ABOUT THIS
CALCULATOR
Visit our Web site.
http://sharp-world.com/calculator/
Means of samples (y data)
y
sy
Sample standard deviation (y data)
y
Population standard deviation (y data)
y
Sum of samples (y data)
y
2
Sum of squares of samples (y data)
Sum of products of samples (x, y)
xy
r
Correlation coefficient
Coefficient of regression equation
a
b
Coefficient of regression equation
c
Coefficient of quadratic regression equation
or
are pressed. Before entering new data, clear the memory
frequency
(To enter multiples of the same
Data y
Data y
frequency
(To enter multiples
:
.
:
. Display the data to correct, press
to delete,
Type
Regression formula
y = a + bx
y = a • e
bx
y = a + b • ln x
y = a • x
b
1
y = a + b —
x
2
y = a + bx + cx
10
100
.
(19) (23)
(or
) automatically moves the cursor
to clear the equation.
Ex. 2
5
100
.
-99
99
±10
– ±9.999999999 10
and 0.
–99
, the value is considered to be 0 in
is pressed in dim lighting, it is time to replace the
.
(Fig. 1)
(Fig. 2)
Scientific calculations, complex number
calculations, simultaneous linear
equations with three unknowns, statistical
calculations, etc.
Mantissas of up to 12 digits
16 calculations 8 numeric values
(4 numeric values in STAT and complex
number mode)
Built-in solar cells
3V
(DC):
Backup batteries (Alkaline batteries (LR44)
2)
78.6 mm (W) 152 mm (D) 10.5 mm (H)
3-3/32″ (W)
5-31/32″ (D)
13/32″ (H)
Approx. 78 g ( 0.172 lb)
(Including batteries)
Batteries
2 (installed), operation
manual, operation examples sheet, quick
reference card (Physical Constants and
Metric Conversions) and hard case
(22)
(24)
