Инструкцию можно записать только для решения математической задачи

23. Тест. Что такое алгоритм Автор: © 2015, ООО КОМПЭДУ, http://compedu.ru при поддержке проекта http://videouroki.net

Алгоритмизация и программирование

Алгоритмы, виды алгоритмов, описание алгоритмов. Формальное исполнение алгоритмов

Термин «алгоритм», впервые употребленный в современном значении. Лейбницем (1646–1716), является латинизированной формой имени великого персидского математика Мухаммеда бен Муссы аль-Хорезми (ок. 783 – ок. 850). Его книга «Об индийском счете» в XII в. была переведена на латинский язык и пользовалась широкой популярностью не одно столетие. Имя автора европейцы произносили как Алгоритми (Algorithmi), и со временем так стали называть в Европе всю систему десятичной арифметики.

Научное определение алгоритма дал А. Чёрч в 1930 году. В наше время понятие алгоритма является одним из основополагающих понятий вычислительной математики и информатики.

Алгоритм — это точное и полное описание последовательности действий над заданными объектами, позволяющее получить конечный результат.

Можно сказать, что алгоритм решения какой-либо задачи — это последовательность шагов реализации (или нахождения) этого решения, а процесс построения алгоритма (алгоритмизация) — разложение задачи на элементарные действия или операции.

Область математики, известная как теория алгоритмов, посвящена исследованию свойств, способов записи, области применения различных алгоритмов, а также созданию новых алгоритмов. Теория алгоритмов находит широкое применение в различных областях деятельности человека — в технике, производстве, медицине, образовании и т. д. Появление компьютера позволило решать чрезвычайно сложные, трудоемкие задачи.

Определение алгоритма для применения в области информатики нуждается в некотором уточнении. Во-первых, решение задач в информатике всегда связано с преобразованием информации, а значит, исходными данными и результатом работы алгоритма должна быть информация. Это может быть представлено в виде схемы.

Во-вторых, алгоритмы в информатике предназначены для реализации в виде компьютерных программ или для создания некоторой компьютерной технологии. Для выполнения алгоритма требуется конечный объем оперативной памяти и конечное время.

Основные требования, предъявляемые к алгоритмам:

Дискретность (прерывность): алгоритм должен представлять решение задачи в виде последовательности простых (или ранее определенных) этапов (шагов). Каждый шаг алгоритма формулируется в виде инструкций (команд).

Определенность (детерминированность; лат. determinate — определенность, точность): шаги (операции) алгоритма должны допускать однозначную трактовку и быть понятными для исполнителя алгоритма. Это свойство указывает на то, что любое действие в алгоритме должно быть строго определено и описано для каждого случая.

Массовость: алгоритм должен давать решение не только для конкретного набора значений, а для целого класса задач, который определяется диапазоном возможных исходных данных (область применимости алгоритма). Свойство массовости подразумевает использование переменных в качестве исходных данных алгоритма.

Результативность: алгоритм должен давать конкретный результат, т. е. должны быть рассмотрены все возможные ситуации и для каждой из них получен результат. Под результатом может пониматься и сообщение о том, что задача решения не имеет.

Конечность: количество шагов алгоритма должно быть конечным.

Эффективность: количество шагов и сами шаги алгоритма должны быть такими, чтобы решение могло быть найдено за конечное и, более того, приемлемое время.

Для оценки и сравнения алгоритмов существует много критериев. Чаще всего анализ алгоритма (или, как говорят, анализ сложности алгоритма) состоит в оценке временных затрат на решение задачи в зависимости от объема исходных данных. Используются также термины «временная сложность», «трудоемкость» алгоритма. Фактически эта оценка сводится к подсчету количества основных операций в алгоритме, поскольку каждая из них выполняется за заранее известное конечное время. Кроме временной сложности, должна оцениваться также емкостная сложность, т. е. увеличение затрат памяти в зависимости от размера исходных данных. Оценка сложности дает количественный критерий для сравнения алгоритмов, предназначенных для решения одной и той же задачи. Оптимальным (наилучшим) считается алгоритм, который невозможно значительно улучшить в плане временных и емкостных затрат.

Анализом сложности алгоритмов, исследованием классов задач, решаемых с помощью алгоритмов той или иной сложности, и многими другими теоретическими вопросами занимается специальная область информатики.

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов.

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур:

1. следование — образуется из последовательности действий, следующих одно за другим;
2. ветвление (развилка) — обеспечивает в зависимости от результатов проверки условия (ДА или НЕТ) выбор одного из альтернативных путей алгоритма;
3. цикл — обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.

Для описания алгоритмов наиболее распространены следующие методы (языки):

Обычный язык. Изложение алгоритма ведется на обычном языке с разделением на последовательные шаги.

Блок-схемы. Графическое изображение алгоритма с помощью специальных значков-блоков.

Формальные алгоритмические языки (языки программирования). При записи алгоритмов используют строго определенный набор символов и составленных из них специальных зарезервированных слов. Имеют строгие правила построения языковых конструкций.

Псевдокод. Синтез алгоритмического и обычного языков. Элементы некоторого базового алгоритмического языка используются для строгой записи базовых структур алгоритма.

Словесный способ (запись на обычном языке) не имеет широкого распространения, т. к. таких описаний есть ряд недостатков:

• строго не формализуемы;
• достаточно многословны;
• могут допускать неоднозначность толкования отдельных предписаний;
• сложные задачи с анализом условий, с повторяющимися действиями трудно представляются в словесной или словесно-формульной форме.

Графический способ представления информации является более наглядным и компактным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление алгоритма называется блок-схемой. Определенному типу действия (ввод/вывод данных, проверка условия, вычисление выражения, начало и конец алгоритма и т. п.) соответствует определенная геометрическая фигура — блочный символ. Блоки соединяются между собой линиями переходов, которые определяют очередность выполнения действий.

Название символа	Графическое изображение	Комментарии
Пуск/Останов (блоки начала и конца алгоритма)		Указание на начало или конец алгоритма
Ввод/Вывод данных (блоки ввода, вывода		Организация ввода/вывода в общем виде
Процесс (операторные блоки)		Выполнение вычислительного действия или последовательности действий (можно объединять в один блок), которые изменяют значение, форму представления или размещение данных
Условие (условный блок)		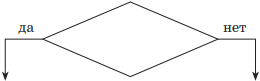Выбор направления выполнения алгоритма. Если условие, записанное внутри ромба, выполняется, то управление передается по стрелке «да», в противном случае — по стрелке «нет». Таким образом, реализуется процесс изменения последовательности вычислений в зависимости от выполнения условия
Начало цикла с параметром		Используется для организации циклических конструкций с известным количеством итераций (повторений) и известным шагом изменения параметра цикла. Внутри блока для параметра цикла указываются через запятую его начальное значение, конечное значение и шаг изменения. Цикл, для которого неизвестно количество повторений, записывается с помощью условного и операторных блоков
Предопределенный процесс		Используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращения к библиотечным подпрограммам
Печать сообщений (документ)		Вывод результатов на печать

При составлении блок-схемы необходимо проверять выполнение следующих условий:

1. из каждого прямоугольника и параллелограмма (кроме конца алгоритма) должна выходить только одна стрелка;
2. в каждый прямоугольник и параллелограмм (кроме начала алгоритма) должна входить хотя бы одна стрелка;
3. в каждый ромб должна входить хотя бы одна стрелка, а выходить из него — две стрелки, помеченные словами «ДА» и «НЕТ».

Псевдокод занимает промежуточное положение между естественным языком и языками программирования. В псевдокоде не приняты строгие синтаксические правила для записи команд, что отличает формальные языки программирования. Однако в псевдокоде есть некоторые конструкции, которые присущи формальным языкам, что облегчает переход от записи алгоритма на псевдокоде к записи алгоритма на языке программирования. Псевдокоды бывают разные. Рассмотрим учебный (школьный) алгоритмический язык АЯ.

Алфавит учебного алгоритмического языка является открытым. В него могут быть введены любые понятные всем символы: русские и латинские буквы, знаки математических операций, знаки отношений, специальные знаки и т. д. Кроме алфавита, в алгоритмической нотации определяются служебные слова, которые являются неделимыми. Служебные слова обычно выделяются жирным шрифтом или подчеркиванием. К служебным словам относятся:

алг — заголовок алгоритма	нц — начало цикла	знач
нач — начало алгоритма	кц — конец цикла	и
кон — конец алгоритма	дано	или
арг — аргумент	надо	не
рез — результат	если	да
цел — целый	то	нет
сим — символьный	иначе	при
лит — литерный	всё	выбор
лог — логический	пока	утв
вещ — вещественный	для	ввод
таб — таблица	от	вывод
длин — длина	до

Общий вид записи алгоритма на псевдокоде:

алг — название алгоритма (аргументы и результаты)

дано — условие применимости алгоритма

надо — цель выполнения алгоритма

нач — описание промежуточных величин

последовательность команд (тело алгоритма)

кон

Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон, — телом алгоритма (исполняемой частью алгоритма).

В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное именем массива и граничными парами по каждому индексу элементов массива.

Команды учебного языка:

1. Оператор присваивания, который обозначается «:=» и служит для вычисления выражений, стоящих справа, и присваивания их значений переменным, указанным в левой части. Например, если переменная а имела значение 5, то после выполнения оператора присваивания а := а + 1, значение переменной а изменится на 6.

2. Операторы ввода/вывода:

ввод (список имен переменных)

вывод (список вывода)

Список вывода может содержать комментарии, которые заключаются в кавычки.

3. Оператор ветвления (с использованием команды если…то… иначе…всё; выбор);

4. Операторы цикла (с использованием команд для, пока, до).

Запись алгоритма на псевдокоде:

Здесь в предложениях дано и надо после знака «|» записаны комментарии. Комментарии можно помещать в конце любой строки, они существенно облегчают понимание алгоритма.

При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается произвольное изображение команд. Вместе с тем такая запись позволяет понять человеку суть дела и исполнить алгоритм. Однако алгоритм, предназначенный для исполнения на компьютере, должен быть записан на строго формализованном языке. Такой язык называется языком программирования, а запись алгоритма на этом языке — компьютерной программой.

Для решения одной и той же задачи можно предложить несколько алгоритмов. Алгоритмы составляются с ориентацией на определенного исполнителя алгоритма. У каждого исполнителя имеется свой конечный набор команд, которые для него понятны и исполняемы. Этот набор называется системой команд исполнителя. Пользуясь системой команд, исполнитель может выполнить алгоритм формально, не вникая в содержание поставленной задачи. От исполнителя требуется только строгое выполнение последовательности действий, предусмотренной алгоритмом. Таким образом, в общем случае алгоритм претерпевает изменения по стадиям:

• первая стадия — алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает;
• вторая стадия — алгоритм должен быть представлен в форме, понятной исполнителю алгоритма (вторая стадия может отсутствовать, если исполнять алгоритм будет сам разработчик).

Примеры решения задач

Пример 1. Исполнитель Утроитель может выполнить только две команды, которым присвоены номера:

1 — вычти 1;

3 — умножь на 3.

Первая команда уменьшает число на 1, вторая — увеличивает его втрое.

Написать набор команд (не более пяти) получения из числа 3 числа 16. В ответе указать только номера команд.

Решение.

1 (3 – 1 = 2)

3 (2 * 3 = 6)

3 (6 * 3 = 18)

1 (18 – 1 = 17)

1 (17 – 1 = 16)

Ответ: 13311

Пример 2. Имеется Исполнитель алгоритма, который может передвигаться по числовой оси.

Система команд Исполнителя алгоритма:

1. «Вперед N» (Исполнитель алгоритма делает шаг вперед на N единиц).

2. «Назад M» (Исполнитель алгоритма делает шаг назад на M единиц).

Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?

Решение.

1. Найдем, сколько было команд «Вперед», а сколько «Назад». Учитывая, что общее количество команд равно 50 и что команд «Назад» на 12 больше, чем команд «Вперед». Получим уравнение: x + (x + 12) = 50, где x — количество команд «Вперед». Тогда общее количество команд «Вперед»: x = 19, а количество команд «Назад»: 19 + 12 = 31.

2. Будем вести отсчет от начала числовой оси. Выполнив 19 раз команду «Вперед 3», Исполнитель алгоритма оказался бы на отметке числовой оси 57 (19 * 3 = 57). После выполнения 31 раз команды «Назад 2» (31 * 2 = 62) он оказался бы на отметке –5 (57 – 62 = –5).

3. Все эти команды можно заменить одной — «Назад 5».

Ответ: команда«Назад 5».

Пример 3. Черепашка является исполнителем для создания графических объектов на рабочем поле. При движении Черепашка оставляет след в виде линии. Черепашка может исполнять следующие команды:

Название команды	Параметр	Действия исполнителя
вп	Число шагов	Продвигается в направлении головы на указанное число шагов
нд	Число шагов	Продвигается в направлении, противоположном направлению головы на указанное число шагов
пр	Число градусов	Поворачивается направо относительно направления, заданного головой черепашки
лв	Число градусов	Поворачивается налево относительно направления, заданного головой черепашки

Для записи повторяющихся действий (цикла) используется команда Повтори. В этой команде два параметра: первый задает количество повторений (итераций), а второй — список команд которые должны повторяться (тело цикла); список заключается в квадратные скобки.

Записать для исполнителя Черепашка алгоритмы:

а) построения квадрата со стороной 100;

б) построения правильного шестиугольника со стороной 50.

в) построения изображения цифры 4, если голова Черепашки смотрит на север.

Ответ: а) Повтори 4 [вп 100 пр 90]; б) Повтори 6 [вп 50 пр 360/6]; в) вп 100; повтори [лв 135 вп 50].

Пример 4. Два игрока играют в следующую игру (это вариант восточной игры). Перед ними лежат три кучки камней, в первой из которых 2, во второй — 3, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в одной из кучек, или добавляет по два камня в каждую из них. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней в трех кучках становится не менее 25. Кто выиграет при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ следует обосновать.

Решение. Удобнее всего составить таблицу возможных ходов обоих игроков. Заметим, что в каждом случае возможны всего четыре варианта хода. В таблице курсивом выделены случаи, которые сразу же приносят поражение игроку, делающему этот ход (например, когда камней в какой-либо кучке становится больше или равно 8, другой игрок непременно выигрывает следующим ходом, удваивая количество камней в этой кучке). Из таблицы видно, что при безошибочной игре обоих игроков первый всегда выиграет, если первым ходом сделает 4, 5, 6. У второго игрока в этом случае все ходы проигрышные.

	1-й ход	2-й ход
Начало	1-й игрок	2-й игрок	1-й игрок	2-й игрок
2,3,4	4,3,4	8,3,4	выигрыш
4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
4,3,8	выигрыш
6,5,6	12,5,6	выигрыш
6,10,6	выигрыш
6,5,12	выигрыш
8,7,8	выигрыш
	2,6,4	4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
2,12,4	выигрыш
2,6,8	выигрыш
4,8,6	выигрыш
2,3,8	выигрыш
4,5,6	8,5,6	выигрыш
4,10,6	выигрыш
4,5,12	выигрыш
6,7,8	выигрыш

Пример 5. Записано 7 строк, каждая из которых имеет свой номер. В нулевой строке после номера записана цифра 001. Каждая последующая строка содержит два повторения предыдущей строки и добавленной в конец большой буквы латинского алфавита (первая строка — A, вторая строка — B и т. д.). Ниже приведены первые три строкиєтой записи (в скобках указан номер строки):

(0) 001

(1) 001001A

(2) 001001A001001AB

Какой символ находится в последней строке на 250-м месте (считая слева направо)?

Примечание. Первые семь букв латинского алфавита: A, B, C, D, E, F, G.

Решение. Найдем длину каждой строки. Длина каждой следующей строки в два раза больше длины предыдущей плюс один символ, длина строк составит:

(0) 3 символа;

(1) 3*2+1=7;

(2) 7*2+1=15;

(3) 15*2+1=31;

(4) 31*2+1=63;

(5) 63*2+1=127;

(6) 127*2+1=255 символов.

Так как задано 7 строк, а нумерация начинается с нулевой строки, последняя строка имеет номер 6 и содержит 255 символов. Последний символ в строке — F. Предпоследний элемент — E, далее идут символы D, C, B, A, 1 (по правилу формирования строк). Таким образом, 250-й символ — это 1.

Ответ: 1.

Пример 6. Имеется фрагмент алгоритма, записанный на учебном алгоритмическом языке:

n := Длина(а)

k = 2

b := Извлечь(а, k)

нц для i от 7 до n – 1

с := Извлечь(а, i)

b := Склеить(b, с)

кц

Здесь переменные а, b, с — строкового типа; переменные n, i — целые.

В алгоритме используются следующие функции:

Длина(х) — возвращает количество символов в строке х. Имеет тип «целое».

Извлечь(х, i) — возвращает i-й символ слева в строке х. Имеет строковый тип.

Склеить(х, у) — возвращает строку, в которой находятся все символы строки х, а затем все символы строки у. Имеет строковый тип.

Какое значение примет переменная b после выполнения этого фрагмента алгоритма, если переменная а имела значение «ВОСКРЕСЕНЬЕ»?

Решение. Находим общее число символов в строке а, получим, что n = 11.

Выполняя команду b := Извлечь(а, k) при k = 2, получим, что b примет значение «О«.

В цикле последовательно, начиная с 7-го символа строки а и заканчивая предпоследним (n – 1), извлекаем символ из строки а и присоединяем к строке b.

В результате получим слово «ОСЕНЬ» (символы с номерами 2 + 7 + 8 + 9 + 10).

Ответ: «ОСЕНЬ«

Пример 7. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который называется его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака», написанной в 1202 году. Он выглядит так:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…

В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составить словесный алгоритм и блок-схему проверки принадлежности введенного числа n ряду Фибоначчи.

Решение. Словесный алгоритм:

1. Ввести число n.
2. Установить значение первых трех чисел Фибоначчи: 1, 1, 2 (сумма двух предыдущих чисел).
3. Пока введенное число n больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи.
4. Если число Фибоначчи равно введенному n или было введено число n = 1, значит, что было введено число Фибоначчи, в противном случае — введенное число не является числом Фибоначчи.

Приведенный словесный алгоритм в пункте 1, 2 содержит начальные установки, в пункте 3 — цикл с условием, а пункт 4 — это вывод результата работы алгоритма.

Блок-схема алгоритма:

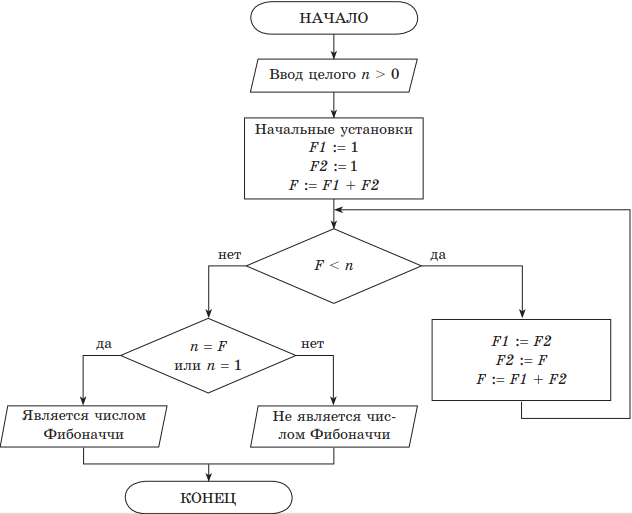
Обозначения:

F — текущее число ряда Фибоначчи;

F1 и F2 — два предыдущих числа ряда Фибоначчи для числа F;

n — число, для которого требуется определить, является ли оно числом из ряда Фибоначчи.

Использование основных алгоритмических конструкций: следование, ветвление, цикл

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.

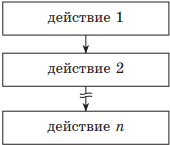
Базовая структура СЛЕДОВАНИЕ указывает на то, что управление передается последовательно от одного действия к другому.

Учебный алгоритмический язык	Язык блок-схем
действие 1 действие 2 … действие n

Использование исключительно этой структуры возможно лишь для достаточно простых задач, ход решения которых не меняется в зависимости от конкретных исходных данных и состоит в последовательном выполнении определенных операций.

В качестве примера рассмотрим решение простой задачи.

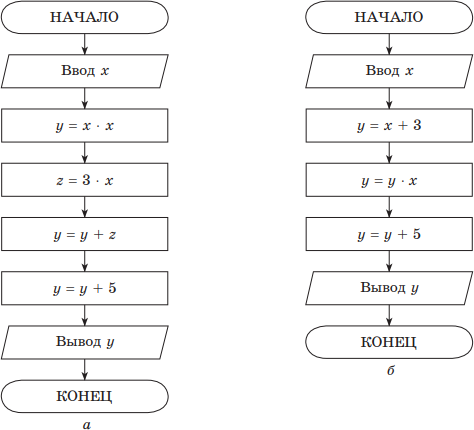
Пример. Найти y(x) = x2 + 3x + 5, используя только операции умножения и сложения.

Решение. На рис. приводятся два алгоритма, реализующие решение поставленной задачи.

Порядок вычисления y(x) в первом случае — обычный, а во втором — (x + 3) x + 5. Обе формулы эквивалентны, но в первом случае для вычисления необходимо 2 умножения, 2 сложения и 3 переменных (x, y, z), а во втором используются 1 умножение, 2 сложения и 2 переменные (x, y).

Приведенный пример показывает, что даже простые задачи могут решаться с помощью различных вариантов алгоритмов.

Обратите внимание, как в блоке следования используется оператор присваивания.

Операция присваивания — важнейшая операция во всех языках программирования. С помощью присваивания переменные получают новые значения: в левой части инструкции ставится идентификатор величины, а в правой части — выражение, значение которого можно определить.

В операторах присваивания используется либо привычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных правой части уже определены.

Базовая структура ВЕТВЛЕНИЕ (РАЗВИЛКА) используется в случае, когда выполнение программы может измениться в зависимости от результата проверки условия и пойти двумя разными (альтернативными) путями. Другими словами, условие является некоторым высказыванием (предикатом) и может быть истинным или ложным (принимать значение TRUE или FALSE). Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.

Различают две структуры этого типа — полную и неполную. В случае полной структуры, если условие выполняется (является истинным), вслед за ним выполняется действие 1, иначе — действие 2. В случае неполной структуры, если условие выполняется (является истинным), то вслед за ним выполняется действие 1, иначе ничего не происходит.

Важную роль в операторах ветвления играют содержащиеся в них условия. В простейшем случае условиями служат отношения между величинами. Условия с одним отношением называют простыми условными выражениями, или простыми условиями. В некоторых задачах необходимы более сложные условия, состоящие из нескольких простых, например условие А < X < С, т. е. Х < А и (Х > C) (возможна запись (Х < А) and (Х > C)). Объединение нескольких простых условий в одно образует составное условное выражение, или составное условие. Составные условия образуются с помощью логических операторов not (отрицание), and (логическое И), or (логическое ИЛИ), хоr (исключающее ИЛИ).

Структура ВЕТВЛЕНИЕ существует в четырех основных вариантах:

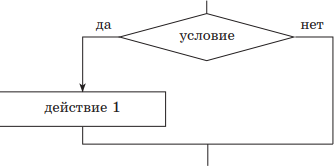
если — то (неполная структура);

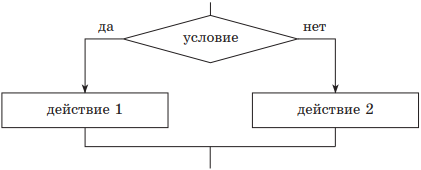
если — то — иначе (полная структура);

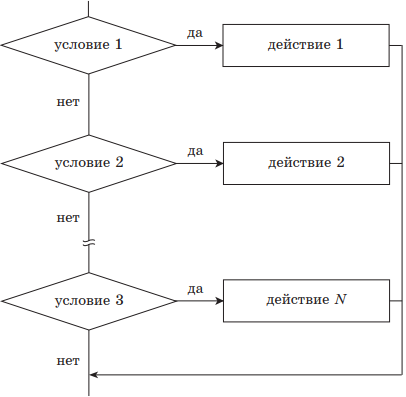
выбор (неполный);

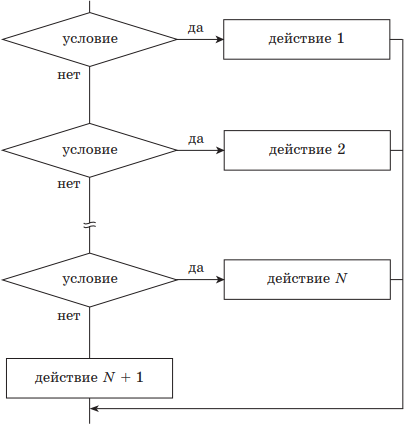
выбор — иначе (полный).

Учебный алгоритмический язык	Язык блок-схем
1) если — то
если условие то действие 1 всё
2) если — то — иначе
если условие то действие 1 иначедействие 2 всё
3) выбор
выбор при условие 1: действие 1 при условии 2: действие 2 … при условие N: действие N всё
4) выбор — иначе
выбор при условие 1: действие 1 при условие 2: действие 2 … при условие N: действие N + 1 иначе действия N + 1 всё

В качестве простого примера рассмотрим нахождение модуля числа y(x) = |x|. Решение приведено на рис. для случаев полной (а) и неполной (б) структур ветвления.

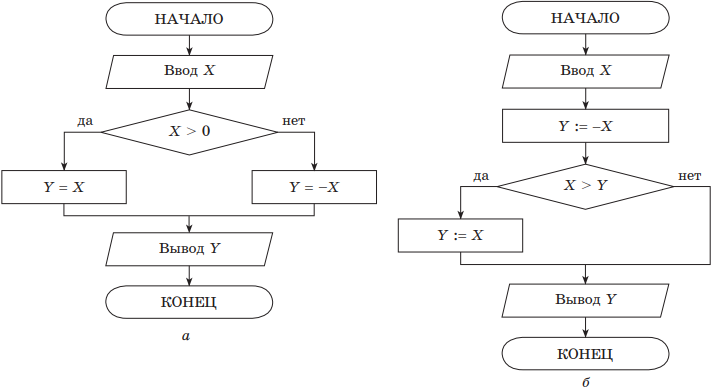
Базовая структура ЦИКЛ служит для записи алгоритмов, в которых некоторая часть алгоритма (тело цикла) должна повторяться несколько раз. Количество повторений цикла может определяться разными способами, в зависимости от которых различают три вида циклов.

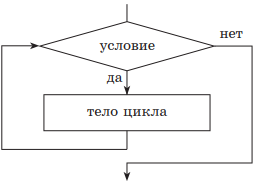
1. Цикл с предусловием, или цикл «пока». При реализации этого цикла сначала проверяется условие его выполнения. Пока оно выполняется, будут происходить повторения тела цикла. Отсюда и другое его название — цикл «пока». Если условие не выполняется при первой проверке, то тело цикла не будет выполняться вообще. После выхода из цикла управление передается следующей структуре. Для того чтобы избежать зацикливания, т. е. бесконечного цикла, в теле цикла обязательно должны изменяться параметры, записанные в условии.

Учебный алгоритмический язык	Язык блок-схем
нц пока условие тело цикла (последовательность действий) кц

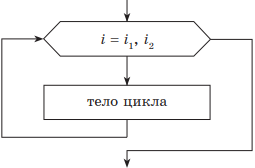
2. Цикл с параметром. Этот вид цикла удобно использовать в тех случаях, когда заранее извесно количество повторений цикла. Вводится понятие счетчика цикла, который по умолчанию считается равным либо 1, либо –1. В некоторых случаях изменение счетчика цикла (приращение) указывают явно. Для организации цикла необходимо задать верхнюю и нижнюю границы изменения счетчика цикла. В зависимости от значения верхней и нижней границы определяется шаг цикла (1 или −1), т. е. значение счетчика цикла.

Учебный алгоритмический язык	Язык блок-схем
нц для i от i1 до i2 тело цикла (последовательность действий) кц

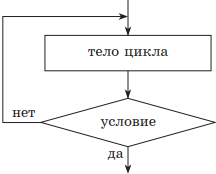
3. Цикл с постусловием, или цикл «до». При реализации этого цикла условие завершение цикла проверяется после тела цикла. В этом случае тело цикла всегда выполняется хотя бы один раз. Цикл будет выполняться до выполнения условия, отсюда и другое название — цикл «до». А пока условие не выполнено, будет повторяться тело цикла (выполнение условия, таким образом, является условием окончания цикла). В этом случае, как и в цикле «пока», необходимо предусмотреть в теле цикла изменение параметров условия цикла.

Учебный алгоритмический язык	Язык блок-схем
нц тело цикла (последовательность действий) до условие кц

Для всех видов цикла предусмотрена возможность досрочного выхода, т. е. прерывание работы цикла.

Помимо трех рассмотренных видов цикла существует и так называемый интерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия. На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата. Классический пример — вычисление суммы ряда с заданной точностью.

Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное условие выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т. е. не будет выполняться основное свойство алгоритма — результативность.

Пример. Вычислить сумму знакопеременного ряда $S=x-{x^2}/{2}+{x^3}/{3}-{x^4}/{4}+…$ с заданной точностью $ε$.

Для данной знакочередующейся бесконечной суммы требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше $ε$.

Решение. Запишем блок-схему алгоритма, где будем использовать следующие обозначения:

$S$ — частичная сумма ряда (стартовое значение равно 0);

$ε$ — точность вычисления;

$i$ — номер очередного слагаемого;

$m$ — значение очередного слагаемого;

$p$ — числитель очередного слагаемого.

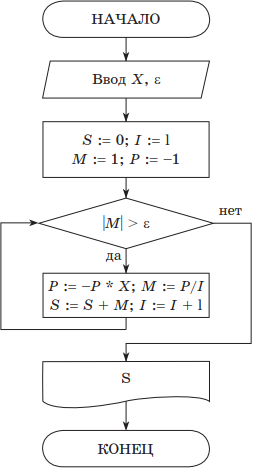
На псевдокоде алгоритм можно записать следующим образом:

Примечание. Следует отметить, что ряд будет сходящимся только при выполнении условия 0 < х < 1.

Возможны случаи, когда внутри тела цикла необходимо повторить некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле, или вложенного цикла. Глубина вложения циклов (количество вложенных друг в друга циклов) может быть различной.

При использовании такой структуры для экономии времени выполнения необходимо выносить из внутреннего цикла во внешний все действия, результаты которых не зависят от параметра внутреннего цикла.

Пример. Вычислить сумму элементов для заданной матрицы (таблицы из 5 строк и 3 столбцов) А(5,3).

Решение. Алгоритм решения задачи на псевдокоде:

Основная часть блок-схемы нахождения суммы элементов матрицы будет иметь следующий вид:

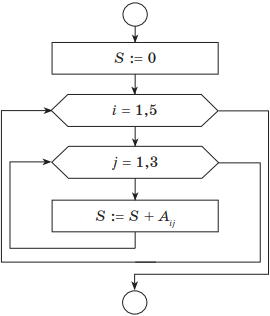
Здесь порядок выполнения вложенных циклов следующий: счетчик внутреннего цикла изменяется быстрее, т. е. для i = 1(внешний цикл), j пробегает значения 1, 2, 3 (внутренний цикл); далее i = 2, j опять пробегает значения 1, 2, 3 и т. д.

Примеры решения задач

Пример 1. Дан фрагмент блок-схемы некоторого алгоритма.

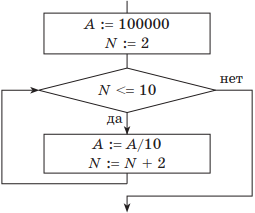
Определить значение переменной А после выполнения фрагмента алгоритма.

Какие исправления нужно внести, чтобы изменение значения переменной А происходило в обратном порядке?

Как записать исходный алгоритм с помощью двух других видов цикла?

Решение. Если представить пошаговое выполнение алгоритма в виде таблицы, получим:

Начальные установки:	A = 100000; N = 2
1-я итерация	A = 10000; N = 4
2-я итерация	A = 1000; N = 6
3-я итерация	A = 100; N = 8
4-я итерация	A = 10; N = 10
5-я итерация, выполнилось условие выхода: N > 10	Ответ: А = 1; N = 12

Таблица обратного хода изменения значения А будет иметь такой вид:

Начальные установки:	A = 1; N = 2
1-я итерация	A = 10; N = 4
2-я итерация	A = 100; N = 6
3-я итерация	A = 1000; N = 8
4-я итерация	A = 10000; N = 10
5-я итерация, выполнилось условие выхода: N > 10	А = 100000; N = 12

Блок-схема алгоритма примет такой вид:

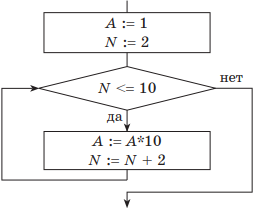
В алгоритме нужно изменить начальное значение А и операцию деления заменить операцией умножения. Счетчик N в данном случае изменять не нужно.

В приведенной в условии блок-схеме используется цикл с предусловием. Для цикла с параметром блок-схема алгоритма будет иметь такой вид:

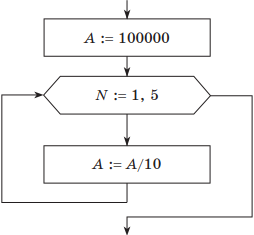
Понятно, что цикл должен выполниться пять раз. В заголовке цикла необходимо указать начальное и конечное значение счетчика цикла N (приращение по умолчанию равно 1).

Для цикла с постусловием блок-схема исходного алгоритма имеет такой вид:

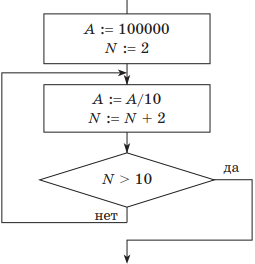
В данной схеме условие завершения цикла находится после тела цикла. Цикл, в отличие от цикла с предусловием, выполняется, пока значение условия ложно.

Пример 2. Сколько раз выполнится тело цикла в программе?

Q := 27; P := 36

нц пока (div(Q, 5) = div(P, 7))

Q := Q + 2

P := P + 3

кц

Примечание. Результат функции div(X, Y) — целая часть от деления X на Y.

Решение. Рассмотрим пошаговое выполнение алгоритма, оформив его в виде таблицы.

Начальные установки	Q := 27; P := 36
Проверка выполнения условия	div(27, 5) = 5; div(36, 7) = 5; 5 = 5
1-я итерация; выполнение тела цикла	Q := 29; P := 39
Проверка выполнения условия	div(29, 5) = 5; div(39, 7) = 5; 5 = 5
2-я итерация; выполнение тела цикла	Q := 31; P := 42
Проверка выполнения условия	div(31, 5) = 6; div(42, 7) = 6; 6 = 6
3-я итерация; выполнение тела цикла	Q := 33; P := 45
Проверка выполнения условия	div(33, 5) = 6; div(45, 7) = 6 6 = 6
4-я итерация; выполнение тела цикла	Q := 35; P := 48
Проверка выполнения условия. Условие не выполняется, цикл завершает работу	div(35, 5) = 7; div(48, 7) = 6; 7 ≠ 6

Ответ: цикл выполнится 4 раза.

Использование переменных. Объявление переменной (тип, имя, значение).
Локальные и глобальные переменные

Величины служат для описания объектов и процессов в материальном мире. Каждая величина имеет некоторые характеристики. В программировании понятие величины несколько отличается от понятия величины в естественных науках — оно является более формальным. Величиной называют объект — переменную, с которым связывается определенное множество значений. Такому объекту присваивается имя — идентификатор. Понятие переменной в программировании сходно с понятием переменной в математике. Например, в алгебраическом равенстве C = F + 2B – 5 значение переменной С зависит от значений переменных F и B, указанных в правой части равенства. Например, при F = 2 и B = 6, С = 9. Такое же равенство можно записать в программе, например на языке программирования Бейсик: C = F + 2*B – 5. В терминах языка программирования C, F и B — это идентификаторы (имена) переменных.

Переменная — это объект программы, имеющий имя и изменяемое значение. Для хранения переменной в памяти компьютера выделено определенное место.

Переменные величины в отличие от постоянных величин (констант) могут со временем менять свое значение. Константой называется величина, которая в ходе выполнения программы не меняет своего значения.

Назначение программы состоит в обработке информации, при этом, конечно, основную роль играют переменные.

Переменная характеризуется:

• идентификатором;
• типом;
• значением.

Каждая переменная имеет свой идентификатор, т. е. свое уникальное имя. Имя переменной показывает, в каком месте памяти компьютера она хранится, значение переменной считывается из указанного ее именем места в памяти. Двух переменных с одним именем в одном программном модуле (блоке) быть не должно. Примерами идентификаторов величин могут быть, например, следующие последовательности символов: a1, SUMMA, X_1, Y_1, My_program.

Во многих языках программирования существуют некоторые ограничения на задания имен переменных. Имена составляются из букв и цифр; первой литерой должна быть буква. Знак подчеркивания «_» считается буквой, его удобно использовать, чтобы улучшить восприятие длинных имен переменных. Разумно давать переменным логически осмысленные имена, в соответствии с их назначением. Нельзя использовать в качестве имен зарезервированные (служебные) слова языка программирования.

Тип переменной — это диапазон (набор) всех значений, которые может принимать данная переменная. Тип переменной определяет, какие операции для нее допустимы. Другими словами, тип переменной — это характеристика, которая для величины определяет:

• необходимый размер памяти;
• диапазон значений, которые может принимать величина;
• возможные операции над величиной (подразумеваются действия относительно использования величин в выражениях);
• формы представления величин (или формат представления величин).

Стандартные типы — это числовые, литерные и логические типы.

Числовой тип, к которому относятся целые и вещественные величины, позволяет оперировать с числами. Целые числа, которые в учебном алгоритмическом языке составляют тип цел, сверху ограничены положительным числом N_max, а снизу — отрицательным числом N_min. Значения N_max и N_min определяются объемом ячеек памяти, в которые записываются целые числа. Обычно для целых чисел выделяется два байта памяти, соответственно границы диапазона равны [N_min = –32768 и N_max = 32767]. Считается, что все операции с величинами типа цел выполняются по обычным правилам арифметики, за одним исключением: возможны две операции деления div и mod.

Операция div обозначает целочисленное деление. При делении с точностью до целых чисел получается два результата — частное и остаток. Знак результата берется по обычным правилам, а полученный остаток игнорируется. Например:

23 div 5 = 4;

2 div 6 = 0;

(–13) div 5 = –2;

(–13) div (–5) = 2.

Операция mod определяет остаток при делении двух целых чисел.

Например:

23 mod 5 = 3;

2 mod 6 = 2;

(–13) mod 5 = –3;

(–13) mod (–5) = 3;

8 mod 2 = 0.

Целые числа чаще всего используются в простых арифметических выражениях и выступают в программах в качестве различных счетчиков и значений индексов.

К другому числовому типу относятся вещественные (вещ) величины. Значения вещественных величин могут изображаться в форме с фиксированной запятой (например, 0,3333; 2,0; –4,567 и т. д.) и с плавающей запятой (например, 7,0*10², 5,173*10^–3 и т. д.).

В отличие от целых чисел, действия с вещественными числами могут быть неточными — это связано с ошибками округлений. Объем памяти, который предоставляется для хранения значений вещественной переменной, — от 4 до 10 байтов (в зависимости от выбранного формата числа). Над числовыми величинами можно выполнять как арифметические операции, так и операции сравнения (>, <, >=, <=, =, ).

Литерный тип, включающий символы и строки, дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов: букв, цифр, знаков препинания, пробела и других специальных знаков (возможными символами могут быть символы таблицы ASCII). Литерные величины обычно заключаются в кавычки: «а», «В», «СТРОКА», «1_2_3». В учебном алгоритмическом языке литерные величины обозначаются как лит. В других языках программирования (например, в Паскале) различают символьный (char) и строковый (string) типы. Величины символьного типа состоят из одного символа и занимают в памяти всего 1 байт. Величины строкового типа представляют собой различные последовательности символов, которые предусмотрены кодовой страницей, установленной в компьютере. Длина строки может составлять от 0 до 255 символов. Над всеми литерными величинами возможны операции сравнения. С помощью отношений типа «a» < «b», «b» < «c», «c» < «d»,… выполняется упорядочение литерных величин (сортировка по возрастанию или убыванию).

Еще одной операцией, характерной для символьных и строковых величин, является операция конкатенации (слияния): «a» + «b» = «ab».

Логический тип позволяет определять логические переменные, которые могут принимать только два значения: истина (true) или ложь (false). Для представления логической величины достаточно одного бита, однако, поскольку место в памяти выделяется по байтам, логической величине отводится минимальная «порция» памяти — один байт. Над логическими величинами можно выполнять все стандартные логические операции.

Значение — это непосредственно то, чему равна переменная в конкретный момент времени. Это может быть число, символ, текст и т. д. Значение переменной в программе можно задать двумя способами: присваиванием и с помощью процедуры ввода.

Оператор присваивания

Во всех языках программирования оператор присваивания является одним из важнейших. С помощью присваивания переменные получают новые значения, например:

Д := 13;

D1 := C;

Х := Х + 1.

В операторах присваивания используется либо обычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных в правой части уже определены и выполняется соответствие типов для правой и левой части оператора присваивания. Например, С := А > B выполнится только в том случае, если для переменной С определен булевский (логический) тип. Операция присваивания может быть применена к большинству типов величин. Однако для каждого из типов предусмотрен свой набор операций.

Локальные, глобальные и общие переменные

Каждая переменная характеризуется областью действия или областью видимости. По зоне видимости в языках программирования различают локальные и глобальные переменные. Первые доступны только конкретному подалгоритму (вспомогательному алгоритму, подпрограмме, модулю), вторые — всему алгоритму (программе). С распространением модульного и объектного программирования появились еще и общие переменные, доступные для определенных уровней иерархии подпрограмм.

Ограничение зоны видимости придумали как для возможности использовать одинаковые имена переменных, так и для защиты от ошибок, связанных с неправомерным использованием переменных.

Имена локальных и глобальных переменных могут совпадать. При этом действует правило: локальные переменные на время работы подпрограмм, в которых они объявлены, экранируют, т. е. перекрывают глобальные переменные. Например, если в основной программе переменная с именем с определена как логическая, а в подпрограмме идентификатор с используется для задания вещественной переменной, то только на время работы подпрограммы с можно использовать как число — в остальных случаях идентификатор с определяет логическую переменную.

Примеры решения задач

Пример 1. Значения заданных переменных А, В перераспределить таким образом, чтобы А и В поменялись значениями.

Решение. Возможны два варианта решения:

С использованием промежуточной переменной С	Без использования дополнительной переменной
C := A; A := B; B := C	A := A + B; B := A – B; A := A – B

Пример 2. Определить значение переменной A после выполнения фрагмента алгоритма:

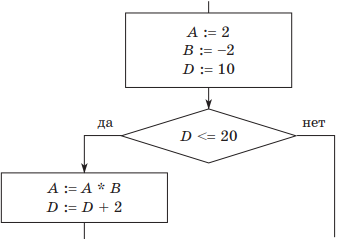
Решение. Оформим решение в виде таблицы.

A	B	D	Условие
2	–2	10	да
–4	–2	12	да
8	–2	14	да
–16	–2	16	да
32	–2	18	да
–64	–2	20	да
128	–2	22	нет — окончание цикла

Ответ: А = 128.

Пример 3. Определить значение переменной S:

A := –1; B := 1

нц пока A + B < 10

A := A + 1; B := B + A

кц

S := A * B

Решение. Оформим решение в виде таблицы.

A	B	A + B	S
–1	1	0
0	1	1
1	2	3
2	4	6
3	7	10 — условие выхода из цикла	21

Ответ: S = 21.

Пример 4. Записать последовательность операций присваивания (:=), которая позволит определить номера подъезда и этажа по номеру N квартиры девятиэтажного дома, считая, что на каждом этаже по 4 квартиры, а нумерация квартир начинается с первого подъезда.

Решение.

4 * 9 = 36 {количество квартир в подъезде}

Х := (N – 1) div 36 + 1 {номер подъезда}

N := N – (X – 1) * 36 { N ∊[1, 36] }

Y := (N – 1) div 4 + 1 {номер этажа}

Например, для квартиры с номером 150 получим:

Х = (150 – 1) div 36 + 1 = 4 + 1 = 5;

N = 150 – (5 – 1) * 36 = 6;

Y = (6 – 1) div 4 + 1 = 2.

Ответ: квартира с номером 150 находится в пятом подъезде, на втором этаже.

Работа с массивами (заполнение, считывание, поиск, сортировка, массовые операции и др.)

Величины числового, литерного, логического типов представляются одним значением и относятся к простым типам данных. Характерной особенностью простых типов является атомарность, т. е. они не могут вмещать элементы других типов. Типы данных, которые не удовлетворяют данному условию, называются структурированными, или составными. Например, массивы, записи, строки, множества, файлы. Структурированный тип характеризуется множеством элементов, из которых складываются данные этого типа. Элементы структурированного типа называются компонентами. В свою очередь компонента структурированного типа может принадлежать также к структурированному типу. Из простых данных сложные структуры могут получаться двумя способами:

1. объединением однородных элементов данных;
2. объединением разнородных элементов данных.

В первом случае примером могут служить массивы, а во втором — записи.

Информацию удобно представлять в виде таблиц. Наиболее привычными являются прямоугольные таблицы, т. е. таблицы, состоящие из строк и столбцов. В том числе таблицы, состоящие из единственной строки или единственного столбца, — линейные таблицы, имеющие одно «измерение».

Табличные величины относятся к составным величинам, т. к. включают в себя другие величины. В учебном алгоритмическом языке табличный тип обозначается как таб. Таблицы в программировании принято называть массивами. В математике прототипом массивов являются матрицы и векторы.

Массив

Массив — это упорядоченный набор данных, имеющий одно имя и состоящий из фиксированного числа однотипных элементов.

Каждый элемент массива снабжен индексом. Индекс — это порядковый номер элемента, определяющий его положение в массиве. Таким образом, элементы массива идентифицируются с помощью имени массива и с помощью своих индексов.

Количество элементов массива называется размерностью массива.

Итак, массив характеризуется:

• размерностью;
• базовым типом элементов;
• типом индекса (может быть только порядковым типом);
• множеством значений для индекса.

Массив может быть одномерным (вектор) и многомерным (матрица).

Одномерный массив содержит одно измерение; каждый элемент массива обозначается идентификатором (именем) массива с индексом. Многомерный массив содержит n-е количество измерений; каждый элемент массива обозначается идентификатором массива для n индексов.

Существует несколько способов заполнения массива данными:

1. непосредственное присваивание значений элементам;
2. заполнение массива произвольными элементами, случайными числами;
3. ввод значений элементов с клавиатуры или чтение из файла.

Необходимо заметить, что заполнение массива происходит поэлементно. Для этого используют оператор цикла. Вывод массива также осуществляется поэлементно с помощью оператора цикла.

Примечание. Строковый тип данных напоминает одномерный массив, в котором элементами являются символы. К примеру, строку «МАМА КУПИЛА ХЛЕБ» можно рассматривать как одномерный массив из 16 символов (включая пробелы). Эту строку можно обозначить идентификатором (например, Novost) и пронумеровать все символы, считая их элементами массива: Novost (l)  = «М», … Novost (16) = «Б».

Однако для работы с символьной информацией более гибким инструментом является не одномерный массив, а строка (string). Это связано с тем, что количество символов в строке, в отличие от массива, не фиксировано. Благодаря этому к строке можно без ограничений применять стандартные операции и функции, предназначенные для работы с текстом.

Задачи, связанные с обработкой массивов, как и все задачи вообще, условно можно разделить на два вида:

1. стандартные задачи;
2. задачи, решение которых требует знания вспомогательных алгоритмов, специальных методов и приемов.

Очевидно, что без умения решать задачи первых двух видов невозможно решать нестандартные задачи.

Стандартные задачи обработки массивов

Пример 1. В массиве А каждый элемент равен 0 или 1. Заменить все нули единицами и наоборот.

Решение. Достаточно одного оператора присваивания в теле цикла:

A[i] := 1 – A[i].

Пример 2. В массиве каждый элемент равен 0, 1 или 2. Переставить элементы массива так, чтобы сначала располагались все 0, затем все 1 и, наконец, все 2. Дополнительный массив не использовать.

Решение. Можно не переставлять элементы массива, а подсчитать количество 0, 1, 2 и заново заполнить массив требуемым образом.

Пример 3. Даны два n-элементных массива Х и Y одного типа. Поменять местами все X_i и Y_i, (i = 1…n), не используя промежуточные величины.

Решение. Обмен можно выполнить в цикле для всех i от 1 до n с помощью серии из трех операторов присваивания:

X[i] := X[i] + Y[i]

Y[i] := X[i] – Y[i]

X[i] := X[i] – Y[i].

Пример 4. Записать алгоритм нахождения максимального элемента массива А(n) и его номера.

Решение. На псевдокоде требуемый алгоритм запишется следующим образом:

Примечание. Если таких элементов несколько, будет найден номер последнего.

Пример 5. Найти сумму элементов одномерного массива А(n).

Решение. На псевдокоде алгоритм нахождения суммы запишется следующим образом:

Примечание. Для нахождения суммы положительных элементов массива вместо оператора

S := S + A[i] необходимо записать:

если A[i] > 0

то S := S + A[i]

всё

Пример 6. Записать алгоритм вычисления произведения элементов столбцов заданной вещественной двумерной матрицы A(n, m).

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 7. Подсчитать количество элементов для заданной целочисленной матрицы A(n, m), равных ее максимальному элементу.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 8. Запиcать алгоритм обмена элементами строк с номерами P и Q в заданной вещественной матрице A(n, m).

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 9. Включить заданное число D в одномерный упорядоченный по возрастанию массив F(n) с сохранением упорядоченности.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 10. Сформировать новый массив B из элементов целочисленного массива A(n), для которых выполняется условие D < A_i < C.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 11. Найти в заданном целочисленном массиве А(m) хотя бы одну пару элементов, совпадающих по значению.

Решение. На псевдокоде алгоритм запишется следующим образом:

Поиск — одна из важных невычислительных задач. Проведение поиска в упорядоченном и неупорядоченном массивах отличается. В неупорядоченном массиве, если нет никакой дополнительной информации об элементе поиска, его выполняют с помощью последовательного просмотра всего массива. Такой поиск называют линейным. В любом случае существуют два условия окончания поиска:

1. элемент найден;
2. весь массив просмотрен — элемент не найден.

В упорядоченном массиве поиск можно значительно ускорить, применяя метод половинного деления, или бинарный поиск. Его идея заключается в следующем. Пусть фиксированный массив упорядочен по неубыванию (a_i ≤ a_{i + 1}). Случайно выбранный элемент am (обычно берут средний элемент) сравнивают с элементом поиска х. Если он меньше х, то искомый элемент может быть среди элементов a_{m + i}, …, а_n, т. е. в правой половине массива. Если он больше х — то среди элементов левой части массива. Если же он равен х, то поиск успешно заканчивается.

К стандартным задачам относятся задачи сортировки массива. Сортировка массива — это перерасположение элементов массива в заданном порядке. Основная цель сортировки — облегчить последующий поиск. Методы условно разделяют по главной идее алгоритма, а реализуются они целым семейством алгоритмов.

К простым методам сортировки относят:

• сортировку с помощью обмена (метод пузырька);
• сортировку с помощью прямого включения;
• сортировку с помощью выбора.

Сортировка с помощью обмена. При использовании этого метода сортировки соседние элементы массива сравниваются и при необходимости меняются местами до тех пор, пока массив не будет полностью упорядочен. Повторные проходы массива каждый раз сдвигают наименьший (наибольший) элемент оставшейся части массива к левому его концу. Метод широко известен под названием «пузырьковая сортировка», т. к. большие (меньшие) элементы массива, подобно пузырькам, «всплывают» на соответствующую позицию. Основной фрагмент программы содержит два вложенных цикла, причем внутренний цикл удобнее выбрать с убывающим шагом.

Алгоритм сортировки массива A(n) по возрастанию на псевдокоде:

Сортировка с помощью прямого включения (вставки). На каждом шаге этого метода массив разделен на две части: левую, уже отсортированную, и правую, еще не отсортированную. Первый элемент правой части вставляется в левую часть массива так, чтобы левая часть осталась отсортированной. В результате отсортированная часть увеличивается на один элемент, а неотсортированная — на один элемент уменьшается. Таким образом, на каждом шаге алгоритма сортировки вставками приходится выполнять две операции: поиск позиции для вставки элемента и собственно его вставку с последующим сдвигом на одну позицию вправо от элементов отсортированной части. Этот сдвиг «стирает» первый элемент неотсортированной части. Сначала отсортированным подмассивом считаем первый элемент, а остальная часть массива относится к неотсортированной части. Поскольку операции сравнения и перемещения чередуются друг с другом, этот способ сортировки часто называют просеиванием или погружением.

Сортировка с помощью прямого выбора. При сортировке этим методом сначала выбирается наименьший (наибольший) элемент массива и меняется местами с первым. Затем выбирается наименьший (наибольший) среди оставшихся (n – 1) элементов и меняется местами со вторым и т. д. до тех пор, пока не останется один наибольший (наименьший) элемент. Сортировка осуществляется с помощью двух вложенных циклов.

Приведенные алгоритмы сортировки не требуют дополнительной оперативной памяти. Время выполнения алгоритмов сортировки пропорционально количеству операций сравнения и перестановки элементов. Сортировка массива из $n$ элементов методом выбора главного элемента требует выполнения ${n^2}/{2}$ операций сравнения и n операций обмена элементами. Метод сортировки вставками требует ${n^2}/{4}$ операций сравнения и столько же операций обмена, а метод пузырьковой сортировки — ${n^2}/{2}$ операций сравнения и столько же операций обмена. Таким образом, из трех рассмотренных методов сортировки массива методы вставки и выбора приблизительно эквивалентны, а обменная сортировка — медленнее. Кроме того, что в методе вставки исходные элементы могут поступать последовательно, а в методе выбора они должны быть в наличии до начала сортировки.

Примеры решения задач

Пример 1. Одномерный массив, содержащий десять элементов, заполняется по следующему закону: A[1] = 1; A[2] = X; A[i] = 2 * X * A[i – 1] – A[i – 2], где i = 3, 4, …, 10. Каким будет значение A[5] при X = 1?

Решение. Представим значения первых пяти элементов массива А, полученные по заданному закону при Х = 1:

A[1] = 1; A[2] = Х = 1;

A[3] = 2 * Х * A[2] – A[1] = 2 * 1 * 1 – 1 = 1;

A[4] = 2 * Х * A[3] – A[2] = 2 * 1 * 1 – 1 = 1;

A[5] = 2 * Х * A[4] – A[3] = 2 * 1 * 1 – 1 = 1.

Таким образом, значение A[5] при Х = 1 будет равно 1.

Ответ: 1.

Пример 2. Задан двумерный массив А(n, n). Определить, что вычисляет приведенный фрагмент алгоритма:

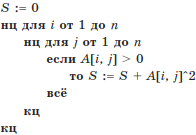
Решение. В данном алгоритме переменной S присваивается значение 0. Затем в структуре циклов по переменным i и j каждый из элементов массива А_ij сравнивается с нулем (А[i, j] > 0) и если элементы А_ij положительны, то квадраты А[i, j]^2 положительных элементов А_ij увеличивают значение суммы S (S := S + A[i, j]^2).

Ответ: фрагмент алгоритма вычисляет сумму квадратов положительных элементов массива.

Пример 3. Задан фрагмент алгоритма, использующий двумерный массив (таблицу) М(n, n), два одномерных массива A(n), B(n) и переменную X. Определить назначение массивов А и В и переменной.

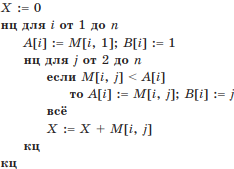
Решение. Представим фрагмент алгоритма словесно.

1. Переменной X присвоить значение 0.
2. Переменной i присвоить значение 1.
3. Если i ≤ n, то перейти к следующему пункту; в противном случае — конец фрагмента алгоритма.
4. Элементу одномерного массива А с индексом i присвоить значение элемента двумерного массива М, находящегося в i-й строке и первом столбце.
5. Элементу одномерного массива В с индексом i присвоить значение 1.
6. Переменной j присвоить значение 1.
7. Если j ≤ n, то перейти к следующему пункту; в противном случае — к п. 13.
8. Если М[i, j] < A[i], то перейти к следующему пункту; иначе — к п. 11.
9. Элементу A[i] присвоить значение элемента массива М, находящегося в i-й строке и j-м столбце.
10. Элементу В[i] присвоить значение переменной j.
11. Переменной Х присвоить значение суммы X + M[i, j].
12. Переменной j присвоить значение суммы j + 1 и вернуться к п. 7.
13. Переменной i присвоить значение суммы i + 1 и вернуться к п. 3.

Таким образом, анализ алгоритма показывает, что переменная X накапливала сумму всех элементов массива М; массив А — минимальные элементы соответствующих строк массива М; массив В — индексы (порядковые номера столбцов) минимальных элементов в соответствующих строках массива М.

Пример 4. Составить алгоритм определения наличия среди элементов главной диагонали заданной целочисленной матрицы A(n, m) хотя бы одного положительного нечетного элемента.

Решение. Для всех элементов А_ij главной диагонали выполняется условие i = j. Определение наличия нечетных элементов выполняется с помощью операции mod (остаток от целочисленного деления), при этом, если результат mod равен 1, — число нечетное.

Алгоритм:

Структурирование задачи при ее решении для использования вспомогательного
алгоритма. Вспомогательные алгоритмы: процедуры и функции

Разработка алгоритмов решения задач на компьютере требует определенных навыков. При построении алгоритма нужно стремиться к тому, чтобы запись алгоритма была понятной и наглядной. Кроме того, внося изменения в алгоритм, желательно не перестраивать его полностью. Эти требования можно удовлетворить, если придерживаться структурного подхода.

Самым важным преимуществом структурного подхода является возможность нисходящего программирования, благодаря которой можно двигаться от крупных задач к более мелким. Крупная задача будет разбиваться на менее крупные блоки, те в свою очередь — на меньшие блоки и т. д. Каждый блок алгоритма должен быть максимально самостоятельным и логически завершенным.

Разбиение на блоки должно определяться внутренней логикой задач. Процесс разбиения завершается, когда решение исходной задачи сводится к решению ряда простых задач, для которых легко построить алгоритм. На каждом шаге этого процесса происходит детализация, т. е. переход от общих задач к частным, которые в свою очередь детализируются в виде конкретных подзадач. Такой метод называется методом пошаговой детализации. Таким образом, при структурном подходе можно комбинировать не только базовые структуры (следование, ветвление, цикл), но и подключать алгоритмы, написанные ранее. Алгоритмы, которые целиком используются в составе других алгоритмов, называются вспомогательными, или подалгоритмами.

Если вспомогательный алгоритм в процессе работы программы выполняется многократно, отличаясь только параметрами, то обычно прибегают к оформлению вспомогательного алгоритма в виде подпрограммы — алгоритма-процедуры, или алгоритма-функции.

Подпрограмма — это именованный, логически законченный алгоритм, который оформляется специальным образом и может многократно использоваться при решении более общей задачи.

Описание подпрограмм можно сравнить с записываемой в математике формулой «в общем виде», в которую при расчетах подставляются конкретные значения. Далеко не каждую задачу можно свести к единственной формуле, но всегда можно записать алгоритм ее решения, а значит, подпрограмма — это инструкция по решению некоторой задачи. Как и формулу, подпрограмму можно использовать для обработки различных данных, передаваемых из главной программы или других подпрограмм.

В языках программирования подпрограмма является частью основной программы, ее описание располагается в описательной части программы. Структура подпрограммы такая же, как и основной программы; различие заключается лишь в оформлении заголовка подпрограммы. Заголовок подпрограммы состоит из служебного слова — идентификатора подпрограммы (имени подалгоритма) — и списка формальных параметров (список параметров не обязателен, допускаются подпрограммы без параметров). При вызове процедуры из текста программы вместо формальных параметров подставляются фактические параметры, при этом соблюдаются следующие правила:

• количество формальных и фактических параметров должно совпадать, причем соответствие между параметрами команды вызова и формальными параметрами процедуры устанавливается по порядку следования: первый фактический параметр соответствует первой переменной, записанной в заголовке подпрограммы, второй фактический параметр — второй переменной и т. д.;
• типы соответствующих параметров команды вызова и заголовка подпрограммы должны совпадать.

Команда вызова подпрограммы выполняется в три этапа:

1. вычисление фактических аргументов;
2. исполнение алгоритма подпрограммы;
3. присвоение полученных значений результатов алгоритма-подпрограммы соответствующим фактическим переменным.

Программа может содержать более одной подпрограммы; допускается использование вложенных подпрограмм, которые, в свою очередь, могут содержать свои вложенные подпрограммы.

Различают два вида подпрограмм — процедуры и функции. Имея один и тот же смысл и аналогичную структуру, процедуры и функции различаются назначением и способом их использования. Основное отличие функций от процедур заключается в том, что результатом выполнения функции является некоторое единственное значение. Функция — это алгоритмически вычисляемое выражение, которое присваивается идентификатору функции.

Подпрограммы бывают двух видов: стандартные и пользовательские. Стандартные, или встроенные, подпрограммы входят в состав языка программирования. Эти подпрограммы определенным образом организованы в специальные библиотеки. С помощью встроенных процедур и функций выполняются операции ввода/вывода, работа с файлами, обработка символьной информации, вычисление различных математических функций и т. п.

Подпрограммы, которые написаны пользователем, называются пользовательскими.

Технология программирования

Чтение короткой (30±50 строк) простой программы на алгоритмическом языке (языке программирования)

Запись алгоритма в словесной форме, в виде блок-схемы или на псевдокоде должна быть точна настолько, чтобы позволить исполнителю правильно выполнить алгоритм, при этом изображение команд произвольное. При решении любой задачи на компьютере предполагается, что некоторая информация подвергается обработке по предварительно составленной инструкции, называемой программой. Язык, на котором записывается алгоритм для исполнения компьютером, называется языком программирования. Языки программирования принадлежат к формальным языкам. При записи алгоритма на языке программирования все правила языка должны строго выполняться. Программа — это алгоритм, записанный на языке программирования.

Для записи программ используется конечный набор символов, составляющих алфавит языка программирования. В отличие от привычных алфавитов (например, русского) алфавит языка программирования включает в себя, кроме букв, цифры, знаки препинания, знаки арифметических действий и некоторые другие дополнительные символы. Программа записывается в виде последовательности символов из алфавита своего языка программирования. Естественно, что не любой текст, составленный из символов алфавита, будет правильной программой. Как и в естественных языках, правильность построения программы из символов алфавита можно проверить, используя синтаксис языка программирования.

Синтаксис языка программирования — это набор правил, которые определяют способы построения правильных программ из символов алфавита. Зная синтаксис языка, можно построить алгоритм, который определяет, является ли данный текст правильной программой или нет. Этот алгоритм позволяет компьютеру проверять синтаксическую правильность вводимых в него программ.

Должна быть определена и семантика языка программирования. Семантика языка программирования — это набор правил, по которым исполнитель выполняет программы на этом языке. Пользуясь семантикой языка, можно однозначно определить результат выполнения программы с заданными входными данными.

При чтении программы необходимо сначала определить, к какому виду она относится. Условно программы можно разделить на два вида: простая программа без использования подпрограмм (кроме стандартных процедур вводавывода) и программа, использующая подпрограммы (подалгоритмы). Такая программа может включать в свою структуру как стандартные подпрограммы, так и подпрограммы, написанные пользователем.

Для чтения простой программы необходимо выяснить:

• что является входными данными и как они вводятся в программу;
• какие действия последовательно выполняются с помощью каждого функционального узла программы (операторов), т. е. рассмотреть пошаговое выполнение операторов, при этом обратить внимание на роль вспомогательных переменных, массивов и т.д.;
• что является результаты работы программы;
• каковы ограничения по работе алгоритма.

При чтении программы, использующей подпрограммы, необходимо сначала проанализировать, что и как выполняют подпрограммы, каковы их входные и выходные параметры. Затем в основной программе вызовы каждой из подпрограмм рассматривать уже как результат работы соответствующего подалгоритма.

Существенно облегчает чтение программ наличие комментариев — поясняющего текста. Комментарии можно добавлять в любое место программы. Наличие комментариев — обязательное условие хорошо и грамотно написанной программы.

Примеры чтения программ на языках Pascal, QBASIC

Примечание. В приведенных примерах программа приводится для двух языков программирования. В зависимости от того, какой язык программирования изучается, и следует рассматривать ее вариант записи и соответствующие пояснения.

Пример 1. Дана программа на двух языках программирования. Определить, какую задачу она решает.

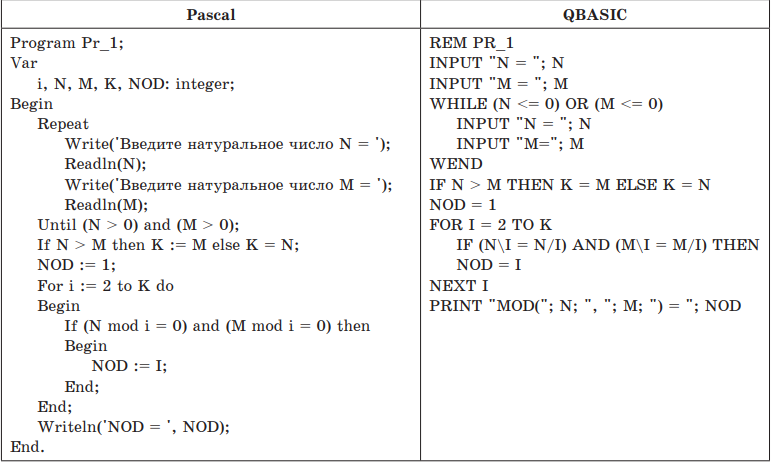
Решение. Проанализируем тексты программы:

1. формируется тело программы и описываются переменные;
2. вводятся натуральные числа М и N, причем проверяется условие корректности ввода: числа должны быть положительные. Если введенные значения не удовлетворяют условию, то ввод повторяют, пока условие не будет выполнено;
3. выбирается наименьшее значение из М и N, результат записывается в K;
4. NOD присваивается значение 1;
5. в цикле от двух до K генерируется число I;
6. тело цикла — в условном операторе проверяется, является ли значение переменной I одновременно делителем М и N. Если условие выполняется, то текущее значение I сохраняется в переменной NOD; если условие не выполняется, NOD не изменит своего значения;
7. после перебора всех значений I в NOD или запишется наибольший делитель двух чисел М и N, или останется значение 1;
8. последний оператор программы служит для вывода результата работы программы — значения переменной NOD.

Переменные, используемые в программе:

N, М — исследуемые числа;

I — переменная цикла;

NOD — наибольший общий делитель;

К — наименьшее из М и N.

Ответ: данная программа позволяет определить для двух чисел М и N их наибольший общий делитель NOD.

Примечание. Эту же задачу можно решить, используя алгоритм Евклида.

Пример 2. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем тексты программы:

1. формируется тело программы, описываются переменные и одномерный массив MAS целого типа (для Pascal целый массив длиной 100);
2. вводится фактическая длина массива N с проверкой на положительное значение N;
3. вводится значение первого элемента массива MAS;
4. устанавливается начальное значение МАХ по первому элементу массива;
5. переменной К присваивается значение 1;
6. последовательно, в цикле, просматриваются вводимые элементы массива, и если очередной элемент MAS(I) больше или равен МАХ, то переписывается значение MAS(I) в МАХ и в переменной К запоминается I;
7. выводятся результаты: МАХ — значение максимального элемента массива и К — номер максимального элемента в исходном массиве (если таких элементов несколько, выведется номер самого правого максимума).

Переменные, используемые в программе:

MAS — массив чисел;

N — размер массива;

I — переменная цикла;

МАХ — значение наибольшего элемента;

К — номер наибольшего элемента.

Ответ: программа написана для поиска значения максимального элемента массива и его номера (если таких элементов несколько, то будет найден номер самого правого максимума).

Пример 3. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем тексты программы:

1. формируется тело программы и описываются переменные;
2. вводится строка символов S;
3. определяется длина строки, значение которой заносится в переменную L;
4. в цикле осуществляется замена ‘!’ на ‘.’ в исходной строке;
5. выводится преобразованная строка.

Переменные, используемые в программе:

I — переменная цикла;

L — длина строки;

S — строка текста.

В программе на языке Pascal используется встроенная функция языка:

Length(STR) — она определяет фактическую длину строки STR (длина строки не более 256 символов).

В программе на языке QBASIC используются встроенные функции:

Len(X) — определяет фактическую длину строки X (длина строки не более 256 символов);

M1D$(X$, N, M) — выделяет M символов, начиная с N-го символа в символьном выражении X$ (M можно опустить).

Ответ: данная программа позволяет заменить во введенной строке символов все восклицательные знаки на точки.

Пример 4. Дана программа на двух языках программирования. Определить, какую задачу она решает.

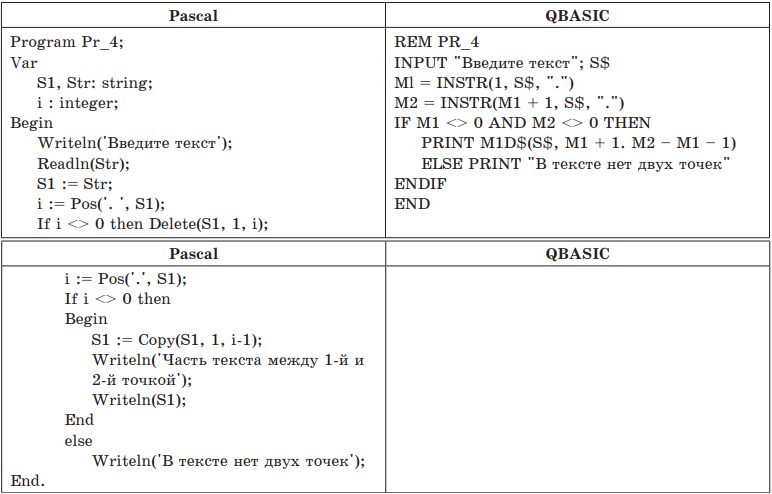
Решение. Проанализируем текст программы на языке Pascal:

1. формируется тело программы и описываются переменные;
2. вводится строка STR и дублируется во вспомогательной переменной S1;
3. определяется местоположение первой точки в тексте; если точка есть, то из S1 вырезается текст до нее;
4. ищется вторая точка; если она есть, то из S1 вырезается текст после нее;
5. в зависимости от присутствия точек результат выводится на экран.

Используемые переменные:

I — номер позиции, которая соответствует точке;

STR — строка текста;

S1 — вспомогательная переменная.

В данной программе используются встроенные функции языка Pascal:

Pos(S1, S2) — поиск подстроки S1 в строке S2 ;

Delete(S, N, M) — удаление из строки S M символов, начиная с позиции N;

Copy(S, N, M) — выделение подстроки из M символов, которые располагаются в строке S начиная с позиции N.

Проанализируем текст программы на языке QBASIC:

1. формируется тело программы, и описываются переменные;
2. вводится строка символов S;
3. определяется местоположение первой точки в тексте — М1;
4. ищется вторая точка в строке (поиск начинается с символа М1 + 1); если в строке есть две точки, то на экран выводится текст, находящийся между двумя точками, если нет — сообщение «В тексте нет двух точек».

Используемые переменные:

S — строка текста;

Ml, M2 — номера позиций двух точек; если точек нет, то значения Ml и М2 равны нулю.

В данной программе используются встроенные функции языка:

INSTR(N, X$, Y$) — поиск подстроки Y в строке X, начиная с N-го символа (N можно опустить);

MID$(X$, N, M) — выделение M символов, начиная с N-го символа в символьном выражении X$ (M можно опустить).

Ответ: данная программа из заданной строки символов выделяет подстроку между первой и второй точкой.

Пример 5. Проанализировать тексты программы.

Решение.

1. Формируется тело программы и описываются переменные и двумерный массив MАS;
2. вводится фактический размер массива MAS и значения его элементов;
3. просматриваются строки массива справа налево, находиться минимальный элемент в строке и запоминаются значения индексов (номер столбца) этого элемента;
4. для каждой строки выводится значение и местоположение самого правого минимального элемента.

Используемые переменные:

MAS — двумерный массив;

N, M — количество строк и столбцов массива;

I, J — переменные цикла;

JM — столбец минимального элемента для данной строки;

MIN — текущий минимум.

Ответ: программа решает задачу поиска в каждой строке двумерной матрицы минимального элемента и его координат. Если таких элементов в строке несколько, то выводится значение и координаты самого правого элемента.

Поиск и исправление ошибок в небольшом фрагменте программы (10±20 строк)

Существует три аспекта проверки программы:

1. на правильность;
2. на эффективность реализации;
3. на вычислительную сложность.

Эти проверки, вместе взятые, направлены на получение экспериментального ответа на вопросы: работает ли алгоритм и насколько хорошо он работает? Предполагается, что проверка правильности удостоверяет, что программа делает в точности то, для чего она была предназначена. Проверка эффективности реализации направлена на поиск способов «заставить» правильную программу работать быстрее или расходовать меньше памяти. Чтобы улучшить программу, пересматриваются результаты этапа реализации в процессе построения алгоритма.

Проверка вычислительной сложности сводится к экспериментальному анализу сложности алгоритма или к экспериментальному сравнению двух или более алгоритмов, решающих одну и ту же задачу.

Наличие ошибок в только что разработанной программе — вполне нормальное, закономерное явление. Составить реальную (достаточно сложную) программу без ошибок практически невозможно. Нельзя делать вывод, что программа правильна, лишь на том основании, что она считает и выдает результаты.

Текст программы можно проконтролировать за столом с помощью просмотра, проверки и прокрутки.

Просмотр. Текст программы просматривается на предмет обнаружения явных ошибок и расхождений с алгоритмом. Нужно просмотреть организацию всех циклов, чтобы убедиться в правильности операторов, задающих кратности циклов. Полезно просмотреть еще раз условия в условных операторах, аргументы в обращениях к подпрограммам и т. п.

Проверка. При проверке программы программист по тексту программы мысленно старается восстановить тот вычислительный процесс, который определяет программа, после чего сверяет его с требуемым алгоритмом.

Прокрутка. Основой прокрутки является имитация программистом за столом выполнения программы на машине. Для выполнения прокрутки приходится задаваться какими-то исходными данными и производить над ними необходимые вычисления.

Прокрутка — трудоемкий процесс, поэтому ее следует применять только для контроля логически сложных участков программы.

После просмотра программы вручную ее необходимо отладить и протестировать на компьютере.

Отладка — это процесс поиска и устранения ошибок в программе, производимый по результатам ее прогона на компьютере.

Тестирование — это испытание, проверка правильности работы программы в целом или ее составных частей.

Отладка и тестирование — два разных этапа:

• при отладке происходит локализация и устранение синтаксических ошибок и явных ошибок кодирования;
• в процессе тестирования проверяется работоспособность программы, не содержащей явных ошибок. Тестирование устанавливает факт наличия ошибок, а отладка выясняет их причину.

Как бы тщательно ни была отлажена программа, решающим этапом, устанавливающим ее пригодность для работы, является контроль программы по результатам ее выполнения на системе тестов. Программу условно можно считать правильной, если ее запуск для выбранной системы тестовых исходных данных во всех случаях дает правильные результаты.

Тестовые данные должны обеспечить проверку всех возможных условий возникновения ошибок. Процесс тестирования можно разделить на три этапа:

1. Проверка в нормальных условиях. Предполагает тестирование на основе данных, которые характерны для реальных условий функционирования программы.
2. Проверка в экстремальных условиях. Тестовые данные включают граничные значения области изменения входных переменных, которые должны восприниматься программой как правильные данные. Типичными примерами таких значений являются очень маленькие или очень большие числа и отсутствие данных. Еще один тип экстремальных условий — граничные объемы данных. Например, когда массивы состоят из слишком малого или слишком большого количества элементов.
3. Проверка в исключительных ситуациях. Проводится с использованием данных, значения которых лежат за пределами допустимой области изменений.

Ошибки могут быть допущены на всех этапах решения задачи. Разновидности характерных ошибок:

• Неправильная постановка задачи — верное решение неверно сформулированной задачи.
• Неверный алгоритм — выбор алгоритма, приводящего к неточному, неэффективному решению задачи.
• Ошибки анализа — неполный учет ситуаций, которые могут возникнуть; логические ошибки.
• Семантические ошибки — неправильный порядок выполнения операций.
• Синтаксические ошибки — нарушение правил, определяемых языком программирования.
• Ошибки при выполнении операций — слишком большое число (переполнение), деление на нуль, извлечение квадратного корня из отрицательного числа и т. п.
• Ошибки в данных — неправильное определение возможного диапазона изменения данных.
• Опечатки — перепутаны близкие по написанию символы, например цифра 1 и буква I.
• Ошибки ввода/вывода — неверное считывание входных данных, неверное задание форматов, отсутствие некоторых данных.

В качестве примера рассмотрим программу, в которой вычисляется значение функции по приведенным формулам в зависимости от значения параметра K, который является номером режима.

$y(x)={table√{a_1x^2+b_1x+c_1}, text»если» K=1; √{a_2x^2+c_2}, text»если» K=2; √{b_3x+c_3}, text»если» K=3;$

Программа имеет вид

Ошибки, допущенные при написании программы:

1. Пропущен ввод исходных данных А1, B1, C1, A2, C2, B3, C3; пропущено описание переменной Y (для языка Pascal).
2. В приведенной программе не предусмотрена обработка ситуации, когда под корнем получается отрицательное значение. Необходимо использовать условный оператор для определения положительности подкоренного выражения.
3. Отсутствует анализ ситуации, когда вместо цифр 1, 2, 3 для переменной К считана другая цифра. В этом случае, можно выдавать, например, сообщение: «Номер режима неверен». Для выдачи такого сообщения в программе в саsе-операторе после строки с меткой 3 нужно добавить строку вида else <Печать сообщения> (вариант 1). Можно также организовать ввод параметра K с проверкой введенного значения, и при ошибочном вводе требовать повторения ввода значения для переменной K (вариант 2).

Пример откорректированной программы (вариант 1).

Пример откорректированной программы (вариант 2).

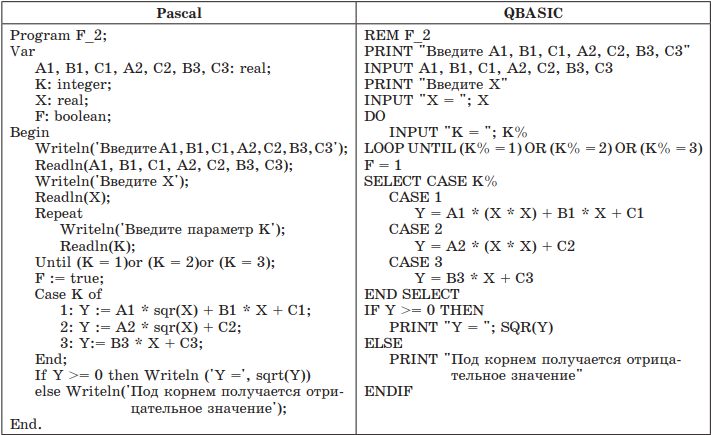
Создание собственной программы (30±50 строк) для решения простых задач

Процесс создания компьютерной модели можно представить как путь от постановки задачи до реализации модели на компьютере. При разработке компьютерной модели очень важен выбор программного обеспечения (ПО), с помощью которого будет реализована модель. Возможны два основных варианта выбора — это, во-первых, прикладное ПО и, во-вторых, среда программирования. Если в качестве ПО была выбрана среда программирования, то построение компьютерной модели завершается созданием программы.

При написании программы прежде всего следует четко уяснить задачу, которую должна решать программа. Затем предварительно разработанный алгоритм решения задачи записывается в виде упорядоченной последовательности команд (инструкций), т. е. составляется программа, ориентированная на определенную среду программирования.

При написании программы обязательно следует проверять, насколько она соответствует намеченной цели, т. е. делает ли программа для всех наборов данных то, что от нее требуется, не выполняет ли она каких-либо лишних действий. Основное внимание следует сосредоточить на предотвращении логических ошибок. Для этого рекомендуется перед написанием программы построить блок-схему алгоритма решения или словесный алгоритм, что позволит абстрагироваться от конкретного языка программирования и сосредоточиться на анализе алгоритма.

Примеры разработки программ

Пример 1. Составить словесный алгоритм, разработать блок-схему и написать программу проверки принадлежности введенного числа данной арифметической прогрессии. Прогрессия задается двумя последовательными членами.

Решение. Словесный алгоритм.

Начало алгоритма

1. Ввести два последовательных члена арифметической прогрессии: A1, A2.
2. Ввести произвольное целое число C.
3. Найти разность (D) арифметической прогрессии.
4. Найти разность между введенным числом C и членом арифметической прогрессии, например A1.
5. Найти остаток от деления нацело найденной разности на D.
6. Если остаток от деления равен 0, то это значит, что число C принадлежит рассматриваемой арифметической прогрессии»; иначе получаем, что число C не принадлежит рассматриваемой арифметической прогрессии.

Конец алгоритма.

Блок-схема алгоритма:

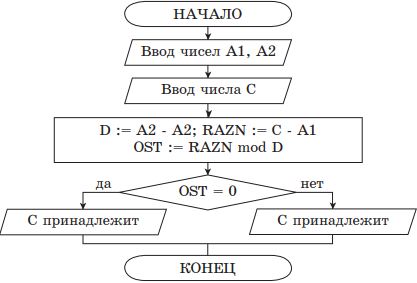
Программа:

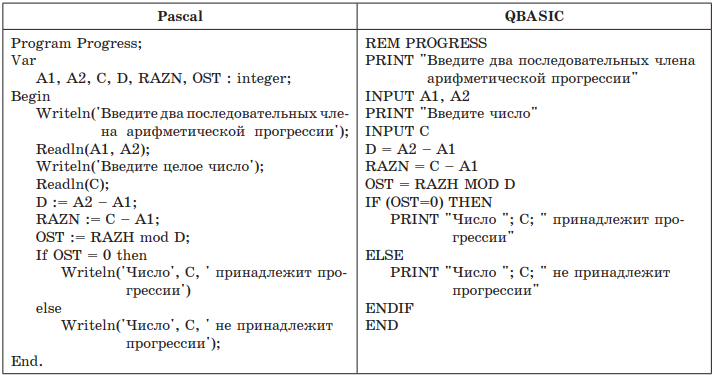
Примечание. Mod — операция, результатом которой является остаток от целочисленного деления.

Пример 2. Составить словесный алгоритм, алгоритм в виде блок-схемы и написать программу поиска в строковом массиве, содержащем фамилии 10 учеников, заданной фамилии, обеспечить запоминание ее порядкового номера (массив фамилий может быть неупорядочен).

Решение.

Словесный алгоритм

Начало алгоритма

1. Ввести все десять фамилий (строковый массив из 10 элементов).
2. Ввести фамилию, которую нужно найти.
3. Сравнивать ее с очередным элементом строкового массива, пока не будет найдена такая же фамилия или пока не закончится список (массив).
4. Если фамилия найдена, вывести ее номер в списке (массиве), если нет — сообщить о том, что фамилия не найдена.

Конец алгоритма.

Блок-схема алгоритма

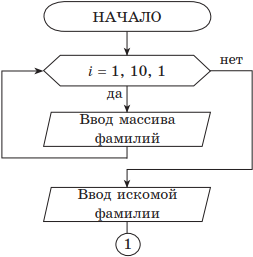
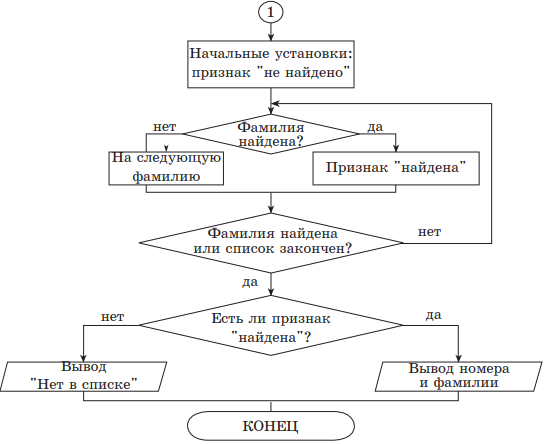
Программа:

§ 5. Основные сведения об алгоритмах

Информатика. 11 класса. Босова Л.Л. Оглавление

---

5.1. Понятие алгоритма.

Задачи, которые мы будем рассматривать в данной главе, достаточно чётко поставлены и формализованы. Основное внимание при их решении мы будем уделять этапам 3-6.

Понятие алгоритма

Каждый из нас ежедневно решает задачи различной сложности: как быстрее добраться в школу или на работу в условиях недостатка времени, в каком порядке выполнить дела, намеченные на текущий день, и т. д. Некоторые задачи настолько сложны, что требуют длительных размышлений для нахождения решения (которое иногда так и не удаётся найти). Другие задачи мы решаем автоматически, т. к. выполняем их ежедневно на протяжении многих лет (выключить звенящий будильник; почистить утром зубы; вскипятить воду в чайнике; позвонить другу по телефону; открыть или закрыть входную дверь ключом). В большинстве случаев в решении каждой задачи можно выделить отдельные шаги.

Пример 1. Решение задачи «Закрыть входную дверь ключом» предполагает выполнение следующих шагов.

1. Вставить ключ в замочную скважину.

2. Повернуть ключ несколько раз на 180 градусов против(по) часовой стрелки(е).

3. Вынуть ключ из замочной скважины.

Последовательность шагов, приведённая в примере 1, является алгоритмом решения задачи «Закрыть входную дверь ключом». Исполнитель этого алгоритма — человек. Объекты этого алгоритма — ключ, дверь.

Для решения любой задачи надо знать, что дано и что следует получить, т. е. у задачи есть исходные данные (объекты) и искомый результат. Для получения результатов необходимо знать способ решения задачи — располагать алгоритмом.

Из курса информатики основной школы вам известны понятия алгоритма и исполнителя.

Исполнитель алгоритма — это субъект или устройство, способные правильно интерпретировать описание алгоритма и выполнить содержащийся в нём перечень действий.

Исполнители бывают двух типов: формальные и неформальные. Далее мы будем говорить преимущественно о формальных или «неразмышляющих» исполнителях. Формальный исполнитель не размышляет над выполняемыми командами, а строго следует пошаговым инструкциям алгоритма. Одну и ту же команду формальный исполнитель всегда выполняет одинаково. За действия формального исполнителя отвечает управляющий им объект.

Алгоритм — это точная конечная система предписаний, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения (после конечного числа шагов) искомого результата.

Приведённое определение не является определением в строгом смысле этого слова, это — описание понятия алгоритма, раскрывающее его сущность. Оно не является формальным, потому что в нём используются такие неуточняемые понятия, как «система предписаний», «действия исполнителя», «объект».

Понятие алгоритма, являющееся фундаментальным понятием математики и информатики, возникло задолго до появления вычислительных машин.

Первоначально под словом «алгоритм» понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.

Пример 2.

Простые числа — это натуральные числа, большие единицы, которые имеют только два делителя: единицу и само это число (рис. 2.1).

Рис. 2.1. Примеры простых чисел (иллюстрация Н. П. Антокольской)

Метод нахождения простых чисел в интервале [2; n] предложил греческий математик Эратосфен (275-194 гг. до н. э.). По одной из версий, он выписал все числа от 2 до 10 ООО на папирусе, натянутом на рамку, и прокалывал составные числа. Папирус стал подобен решету, которое «просеивало» составные числа, а простые оставляло. Поэтому метод Эратосфена называют ещё Эратосфеновым решетом.

Во все времена люди хотели найти как можно большее простое число.

Пока люди считали только при помощи карандаша и бумаги, им нечасто удавалось обнаружить новые простые числа. До 1952 г. самое большое известное простое число состояло из 39 цифр.

В 2013 г. открыто простое число, запись которого в десятичной системе счисления состоит из 17 425 170 знаков. На проверку простоты нового числа ушло 39 дней работы персонального компьютера в Университете Центрального Миссури, США.

Числа, остающиеся незачёркнутыми после завершения работы алгоритма, и есть все простые числа от 2 до n.

На практике, алгоритм можно улучшить следующим образом. На шаге 3 числа можно зачёркивать начиная сразу с числа р² (р • р), потому что все составные числа меньше него к этому времени уже будут зачёркнуты. И соответственно, останавливать алгоритм можно, когда р² станет больше, чем n.

Любой алгоритм существует не сам по себе, он всегда предназначен для определённого исполнителя. Алгоритм описывается в командах исполнителя, который этот алгоритм будет выполнять. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.

Свойства алгоритма.

Значение слова «алгоритм» очень похоже по значению на слова «рецепт», «метод», «способ». Но, в отличие от рецепта или способа, любой алгоритм обязательно обладает следующими свойствами.

1. Дискретность. Выполнение алгоритма разбивается на последовательность законченных действий-шагов. Только выполнив одно действие, можно приступать к выполнению следующего. Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма, называемое командой.

2. Детерминированность. Каждая команда алгоритма определяет однозначное действие исполнителя и недвусмысленно указывает, какая команда должна выполняться следующей. Если алгоритм многократно применяется к одному и тому же набору входных данных, то каждый раз получаются одинаковые промежуточные и выходной результаты.

3. Понятность. Алгоритм не должен содержать предписаний, смысл которых может восприниматься исполнителем неоднозначно, т. е. запись алгоритма должна быть настолько чёткой и полной, чтобы у исполнителя не возникло потребности в принятии каких-либо самостоятельных решений. Стоит помнить, что алгоритм всегда рассчитан на выполнение «неразмышляющим» исполнителем.

4. Результативность. Под этим свойством понимается содержательная определённость результата каждого шага и алгоритма в целом. При точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть и установление того факта, что задача решений не имеет. Свойство результативности содержит в себе свойство конечности — завершение работы алгоритма за конечное число шагов.

5. Массовость. Алгоритм пригоден для решения любой задачи из некоторого класса задач, т. е. алгоритм правильно работает на некотором множестве исходных данных, которое называется областью применимости алгоритма.

Докажите, что рассмотренный в примере 2 метод Эратосфена является алгоритмом.

Не любой расписанный по шагам способ решения задачи является алгоритмом. Убедимся в этом на примере.

Рис. 2.2. Построение перпендикуляра к прямой

Почему этот способ построения перпендикуляра к прямой не является алгоритмом? Какое свойство алгоритмов здесь нарушено?

Есть задачи, которые человек успешно решает, но при этом не может представить процесс их решения в виде последовательности шагов.

Например, если перед человеком положить фотографии собак и кошек и попросить определить, на каких фотографиях изображены собаки, а на каких кошки, то человек практически мгновенно и безошибочно решит эту задачу. Написать же формальный алгоритм решения этой и подобных ей задач пока что не удалось, хотя определённые успехи в этой области, называемой теорией распознавания образа, уже достигнуты.

В супермаркетах вы видите системы распознавания штрих-кодов, используете системы оптического распознавания символов, знаете о распознавании автомобильных номеров, слышали о распознавании изображений лиц, речи и т. д.

Технические системы распознавания образов находят сегодня широкое применение в самых разных областях — от военного дела и систем безопасности до оцифровки аналоговых сигналов. Их разработка базируется на теории распознавания образов — разделе информатики и смежных дисциплин, развивающем основы и методы классификации и идентификации предметов, явлений, процессов, сигналов, ситуаций и тому подобных объектов, характеризующихся конечным набором некоторых свойств и признаков.

С учётом рассмотренных свойств алгоритма можно дать более формальное определение этого понятия, которое также не является строгим, т. к. в нём всё ещё используются не определяемые точно термины.

Алгоритм — это конечная система правил, сформулированных на языке исполнителя, которая определяет последовательность перехода от допустимых исходных данных к конечному результату и обладает свойствами дискретности, детерминированности, понятности, результативности, конечности и массовости.

Математики достаточно долго пользовались интуитивным (нестрогим) понятием алгоритма, записывая алгоритмы примерно так, как в примере 3. Ими были сформулированы многие успешно применяемые на практике алгоритмы решения таких задач, как выполнение арифметических действий «столбиком», нахождение корней квадратных и кубических уравнений, решение систем линейных уравнений и др. Постепенно математики подходили к постановке и решению всё более сложных задач, требовавших построения формального определения алгоритма.

Попытки разработать формальное определение алгоритма привели в 20-30-х годах XX века к возникновению теории алгоритмов — науки, изучающей общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. Вместе с математической логикой теория алгоритмов образует теоретическую основу вычислительных наук.

Математики (А. Тьюринг, Э. Пост, А. Н. Колмогоров, А. А. Марков и др.) предложили несколько подходов к формальному определению алгоритма: нормальный алгоритм Маркова, машина Тьюринга, машина Поста и т. д. Дальнейшее показало, что все эти определения эквивалентны. На основании этих определений учёные пришли к выводу о существовании алгоритмически неразрешимых задач — задач, для которых невозможно построить процедуру решения.

5.2. Способы записи алгоритма

Выбор способа записи алгоритма зависит от ряда причин. Небольшой алгоритм можно записать и в словесной форме. Если для вас наиболее важна наглядность, то разумно использовать блок-схему. Алгоритм же, готовый к реализации, должен быть записан на языке, понятном исполнителю.

Правила выполнения блок-схем, внешний вид графических блоков и их назначение определяются стандартом ГОСТ 19.701-90 (ИСО 5807-85) «Схемы алгоритмов, программ, данных и систем. Обозначения условные и правила выполнения».

Напомним основные условные графические обозначения (символы), которые мы будем использовать в дальнейшем (табл. 2.1).

Таблица 2.1

Основные символы блок-схем и отображаемые ими функции

Пример 4. Вспомним детскую игру «Угадай-ка». Первый игрок задумывает целое число и сообщает второму игроку, из какого оно диапазона. Второй игрок должен как можно быстрее угадать загаданное число. Второй игрок может называть числа, а первый должен говорить, меньше или больше названное число задуманного. Игра заканчивается, если названо число, равное задуманному.

Пусть задумано число X ? [А, В]. Представим в виде блок-схемы алгоритм решения этой задачи — известный вам метод половинного деления (рис. 2.3).

Рис. 2.3. Метод половинного деления

Подсчитайте, какое наибольшее число шагов может понадобиться для угадывания по этому алгоритму числа X ? [0, 100].

5.3. Понятие сложности алгоритма

В теории алгоритмов установлено, что для задачи, имеющей алгоритмическое решение, можно придумать множество различных способов её решения, т. е. алгоритмов.

Какой же алгоритм лучше подходит для решения конкретной задачи? По каким критериям его следует выбирать из множества возможных?

Человек может назвать алгоритм сложным и запутанным из-за того, что тот обладает разветвлённой логической структурой, содержащей много проверок условий и переходов. Однако для компьютера выполнение программы, реализующей такой алгоритм, не составит труда, т. к. он выполняет одну команду за другой, и для компьютера неважно — операция ли это умножения или проверка условия.

Теория алгоритмов предоставляет аппарат анализа различных алгоритмов решения одной и той же задачи, на основе которого можно выбрать самый эффективный (наилучший) алгоритм.

Вычислительным процессом, порождённым алгоритмом, называется последовательность шагов алгоритма, пройденных при его исполнении.

Сложность алгоритма — количество элементарных шагов (действий) в вычислительном процессе этого алгоритма.

Обратите внимание, в определении сложности алгоритма речь идёт именно о вычислительном процессе, а не о самом алгоритме.

Алгоритм состоит из команд.

Команда — это отдельная инструкция в описании алгоритма. Шаг алгоритма — это отдельное действие, которое исполнитель выполняет по команде. В циклических алгоритмах за счёт повторного выполнения одних и тех же команд число шагов при выполнении алгоритма может быть значительно больше числа команд в алгоритме.

Очевидно, что в наибольшей степени число операций при выполнении алгоритма зависит от количества обрабатываемых данных. Действительно, для упорядочивания по алфавиту списка из 100 фамилий требуется существенно меньше операций, чем для упорядочивания списка из 100 000 фамилий. Поэтому сложность алгоритма выражают в виде функции от объёма входных данных.

Так, например, алгоритм, выполняющий только операции чтения данных и занесения их в оперативную память, имеет линейную сложность O(n) (читается «о большое от эн»). Существуют алгоритмы, имеющие квадратичную и кубическую сложности.

Для решения задачи могут быть разработаны алгоритмы, имеющие разную сложность. Лучшим среди них считается алгоритм, имеющий наименьшую сложность.

Наряду со сложностью важной характеристикой алгоритма является эффективность. Эффективность оценивается количеством элементарных операций, которые необходимо выполнить для решения задачи, а также количеством памяти, требующейся для выполнения алгоритма.

Пример 5. Известно, что во многих языках программирования нет операции возведения в степень, и поэтому такой алгоритм программисту надо писать самостоятельно. Операция возведения в степень реализуется через операции умножения. С ростом показателя степени растёт количество операций умножения, которые выполняются достаточно долго. Следовательно, актуален вопрос о создании эффективного алгоритма возведения в степень.

Воспользуемся этим алгоритмом для того, чтобы возвести х в степень n = 100.

1. 100 = 1100100₂.

2. Строим последовательность: КХКХКККХКК.

3. Вычёркиваем крайнюю левую пару КХ: КХКККХКК.

Мы вычислили сотую степень числа х за 8 умножений. Это значительно эффективнее «прямолинейного» алгоритма возведения в степень, требующего 99 операций умножения.

САМОЕ ГЛАВНОЕ

Алгоритм — это конечная система правил, сформулированных на языке исполнителя, которая определяет последовательность перехода от допустимых исходных данных к конечному результату и обладает свойствами дискретности, детерминированности, понятности, результативности, конечности и массовости.

Исполнитель алгоритма — это субъект или устройство, способные правильно интерпретировать описание алгоритма и выполнить содержащийся в нём перечень действий.

Один и тот же алгоритм может быть записан разными способами: на естественном языке, псевдокодом, с помощью блок-схем, на языке программирования и т. д.

Для задачи, имеющей алгоритмическое решение, можно придумать множество различных способов её решения, т. е. алгоритмов. Теория алгоритмов предоставляет аппарат анализа различных алгоритмов решения одной и той же задачи, на основе которого можно выбрать самый эффективный (наилучший) алгоритм.

Алгоритм состоит из команд. Команда — это отдельная инструкция в описании алгоритма. Шаг алгоритма — это отдельное действие, которое исполнитель выполняет по команде. Вычислительным процессом, порождённым алгоритмом, называется последовательность шагов алгоритма, пройденных при его исполнении.

Сложность алгоритма — количество элементарных шагов (действий) в вычислительном процессе этого алгоритма. Наряду со сложностью важной характеристикой алгоритма является эффективность. Эффективность оценивается количеством элементарных операций, которые необходимо выполнить для решения задачи, а также количеством памяти, требующейся для выполнения алгоритма.

---

Вопросы и задания

1. Перечислите основные свойства алгоритмов и проиллюстрируйте их примерами.

2. Почему кулинарный рецепт приготовления торта нельзя считать алгоритмом? Какими свойствами алгоритма он не обладает?

3. Переформулируйте описание способа проведения перпендикуляра к прямой в заданной точке так, чтобы оно стало алгоритмом.

4. Есть двое песочных часов: на 3 и на 8 минут. Для приготовления эликсира бессмертия его надо варить ровно 7 минут. Как это сделать?

5. Исполнитель Вычислитель получает на вход целое число х и может выполнять с ним преобразования по алгоритму, состоящему из любого количества команд: 1) прибавить 5; 2) вычесть 2.

6. Как известно, для каждого исполнителя набор допустимых действий всегда ограничен, иначе говоря, не может существовать исполнителя, для которого любое действие является допустимым. Докажите это утверждение, предположив, что такой исполнитель существует.

7. Перечислите известные вам способы записи алгоритмов.

8. Приведите примеры задач и оптимальных способов записи алгоритмов их решения.

9. Исполнитель Автомат получает на вход четырёхзначное число. Это число он преобразует по следующему алгоритму

10. Подготовьте краткое сообщение об одном из учёных (А. Тьюринг, Э. Пост, А. Н. Колмогоров, А. А. Марков и др.), внёсших вклад в развитие теории алгоритмов.

11. В чём отличие шага алгоритма от команды алгоритма? Приведите пример.

12. Что такое сложность алгоритма? От чего она зависит в наибольшей степени?

13. Подсчитайте сложность алгоритма перемножения двух натуральных чисел «столбиком» при условии, что одно из них состоит из n, а второе — из m десятичных цифр.

14. Какой алгоритм считается эффективным?

15. Постройте эффективный алгоритм возведения числа х в степень n = 152.

---

§ 4. Инструменты анализа данных
Глава 2. АЛГОРИТМЫ И ЭЛЕМЕНТЫ ПРОГРАММИРОВАНИЯ
§ 5. Основные сведения об алгоритмах
§ 6. Алгоритмические структуры

---

Что такое алгоритм.

Тема: «Программирование ветвлений. Условный оператор».

Класс: 9 А.

Продолжительность: 40 минут.

Тип урока: формирование ЗУН.

Форма урока: комбинированный.

Формы работы: фронтальная, индивидуальная, групповая.

Методы обучения: информационно-репродуктивный (объяснительно-иллюстративный), инструктивно-практический; эвристический (частично-поисковый).

Цель урока: сформировать у учащихся представление об условном операторе в языке Pascal и возможностях его применения при решении практических задач.

УУД

• Личностные УУД

— Стимулировать учащихся к саморазвитию;

— развивать готовность и способность к самостоятельности;

— развивать умение ориентироваться в межличностных отношениях.

• Регулятивные УУД

— Самостоятельно формулировать тему урока;

— составлять план и последовательность действий;

— Осуществлять итоговый и пошаговый контроль.

• Познавательные УУД

— Применять правила;

— ориентироваться в разнообразии способов решения задач;

— контролировать и оценивать процесс и результат деятельности;

— самостоятельно составлять алгоритмы при решении задач разного характера.

• Коммуникативные УУД

— составлять вопросы;

— обращаться за помощью;

— формулировать свои затруднения;

— предлагать помощь и сотрудничество.

Планируемые результаты: Знать; структуру оператора ветвления в Паскале, с применением знаний о разветвляющемся алгоритме;

Уметь: решать практические задачи с составление программ на языке Паскаль, содержащие оператор ветвления.

Материально-техническое оснащение:

• Учебник;

• Тетрадь;

• Компьютер;

• Мультимедийный проектор и экран;

• Раздаточный материал;

• Доска.

План урока.

1. Организационный момент (1 минута).

2. Актуализация внимания и знаний(3 минуты).

3. Проверка домашнего задания (5 минут).

4. Объяснение нового материала (10 минут).

5. Физкультминутка (2 минуты).

6. Закрепление изученного материала (10 минут).

7. Домашнее задание (1 минута)

8. Контроль усвоения ЗУН (3 минуты)

9. Рефлексия (2 минуты).

10. Итоги урока (2 минуты).

11. Окончание урока (1 минута).

Ход урока.

1. Организационный момент (1 минута).

Приветствие класса и учителя, класса и гостей. Проверка готовности класса к урока (наличие необходимых школьных принадлежностей). Проверка отсутствующих на уроке.

1. Актуализация внимания и знаний(3 минуты).

Романтические 1960-е годы положили начало дружбе голландца Эдсгера Дейкстры, англичанина Энтони Хоара и швейцарца Никлауса Вирта.

1 ученик. «… Помнятся года, когда мне надо было сделать выбор – либо прекратить программировать и стать настоящим респектабельным теоретическим физиком, либо как-то формально завершить моё обучение теоретической физике с минимальными усилиями и стать… Кем же? Программистом? Но разве это респектабельная профессия? В конце- концов, что такое программирование? В чём должен был состоять тот солидный объём знаний, который позволил бы считать программирование научной дисциплиной?».

2 ученик. «Ваши опасения, Эдсгер, были очевидны, ведь когда компьютеров ещё не было, то программирование не составляло никакой проблемы. Когда у нас появилось несколько маломощных компьютеров, то программирование стало проблемой средней сложности. Теперь же, когда мы располагаем гигантскими компьютерами, то и программирование превращается в гигантскую проблему. Как Вы считаете, Никлаус?».

3 ученик «Да-да, я совершенно с вами согласен. Сейчас мы живём в сложном мире и стараемся решать сложные по своей сути проблемы, которые зачастую для своего решения требуют сложных устройств. Однако, это не значит, что мы не должны найти элегантные решения, убеждающие своей ясностью и эффективностью. Простые элегантные решения более эффективны, но найти их труднее, чем сложные, и для этого требуется больше времени».

И они нашли простое элегантное решение став патриархами структурного программирования и лауреатами премии Тьюринга, приравниваемой в компьютерных науках к Нобелевской премии.

Структурное программирование – подход, при котором для передачи управления в программе используется только 3 инструкции, допускающих последовательную, условную и циклическую передачу данных.

Скажите, какую Структуру передачи данных из этих 3 мы с вами уже изучили? (последовательную.).

Сегодня мы с вами продолжим изучать основы структурного программирования. А для того, чтобы понять какую именно, вам надо разгадать ребус. (Формулирование учениками при помощи учителя темы урока).

Да, мы с вами сегодня изучим структуру «ветвление» на языке Паскаль, который , как вам уже известно, был разработан в конце 60-х годов Н. Виртом. (Дети записываю число и тему урока).

Цели нашего сегодняшнего урока

— Познакомиться с понятием «Условный оператор»;

— Научиться составлять программы на языке Паскаль с использование условного оператора;

— Научиться решать практические задачи, содержащие структуру «ветвление» на ЭВМ в среде программирования PASCAL ABC.

1. Проверка домашнего задания (5 минут).

Но прежде чем мы приступим к изучению новой темы, я предлагаю вспомнить прошлый материал. Откройте свои тетради и выполняем 1- задание.

Задание 1.

Произведите сортировку данных свойств в соответствии с их отношением к свойствам информации или к свойствам алгоритма.

Свойства

алгоритмов

Свойства

информации

Понятность, полезность, массовость, актуальность, полнота, дискретность, результативность, детерминированность, конечность, достоверность.

Сверяем с доской. У кого всё совпало ставит себе 5 баллов, у кого 1 ошибка – ставит 4 балла, 2 ошибки – 3 балла, 3 ошибки – 2 балла, 4 ошибки – 1 балл, более 4 ошибок – 0 баллов.

Переходим к заданию 2.

Заполняется с учителем.

Задание 3.

Составьте четыре правильные по смыслу фразы, соединив их стрелками.

7. Словесный, графический и на алгоритмическом языке

1. Исполнителем алгоритма может быть

6. Для решения целого класса задач

1. Четкое предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи

2. Называется программой

7. Называется системой команд исполнителя

8. Можно составить разные алгоритмы

8. Линейный, разветвляющийся или циклический

5.Называется алгоритмом

4. Основные алгоритмические структуры:

3. Набор действий, которые может выполнить исполнитель

2. Один и тот же алгоритм может быть использован

3. Для решения одной задачи

9. Можно записать только одним способом

4. Любой объект живой природы или автоматическое устройство

9. Называется программой

10. Каждый алгоритм

10. Для решения только одной задачи

5. Алгоритм записанный на языке программирования

11. Можно записать разными способами

6. Только человек

11. Словесный, графический и на алгоритмическом языке

После выполнения задания, учащиеся обмениваются тетрадями и сверяют с доской.4 совпадения – 4 балла, 3 совпадения – з балла, 2 совпадения – 2 балла, 1 совпадение – 1 балл. Если совпадений нет – 0 баллов.

1. Объяснение нового материала (10 минут).

Перед объяснением нового материала выполняется упражнение на стимуляцию слуха.

Это упражнение улучшает слух, кроме того, после него начинает отчетливей восприниматься собственный голос. В некоторых случаях подобный массаж ушей даже вызывает из памяти информацию, которую мы перед этим напрасно пытались вспомнить. Это упражнение должно повторяться как можно чаще.
• Возьмите обеими руками внешнюю часть уха, и потяните туда-сюда очень бережно.
• Массируйте край уха и немного выверните его наружу, начните с верха уха, а потом, медленно массируя, перемещайтесь вниз. Теперь сложите средним указательным пальцем обеих рук букву V. Приложите оба пальца к голове, так ухо оказалось в середине. Начните двигать пальцами вверх-вниз, крепко прижимая их к голове. А затем сделайте из пальцев другой руки полушарие и прикройте им ухо. Потом кончиками пальцев другой руки пару раз постучите по этому куполу. Почувствуйте хлопки в костях черепа, таким образом, вы возбуждаете не только нервы уха, но и мозг.
• Повторите то же самое с другим ухом

Ребята, эпиграф нашего урока «Хочешь быть альпинистом – иди в горы. Хочешь быть образованным – учись мыслить и думать.» Я прошу вас во время объяснения нового материала не только слушать меня, но обдумывать сказанное мною, анализировать.

Алгоритмическая структура «ветвление» в отличие от линейных алгоритмов, в которых команды выполняются одна за другой, входит условие, в зависимости от выполнения или не выполнения которого реализуется та или иная последовательность команд (серия).

Возникает вопрос. Что же такое условие?

Условие – это логическое выражение, которое может быть записано в операторе явно или вычислено в программе.

Виды условия.

последовательные

вложенные

Сложные

(составные)

Простые

Сложные условия – логические выражения, записанные с помощью логических операций not – инверсия (отрицание), and – конъюнкция (умножение), or – дизъюнкция (сложение).

Любой алгоритм можно записать 3-мя способами – словесный, графический, программный.

Словесный – естественная устная или письменная речь,

Графический (блок-схема) – изображение алгоритма при помощи геометрических фигур (дети записывают название и зарисовывают).

Программный – использование операторов языков программирования.

Условному оператору отвечают 2 структуры, выбор которых зависит от формы ветвления

Формы ветвления.

сокращённая

полная

Начнём с полной формы условного оператора. Если , то , иначе. Заменяем слова ЕСЛИ, ТО, ИНАЧЕ на зарезервированные в Паскале слова, получим оператор полного ветвления.

If then else .

Рассмотреть пример.

Сокращённая форма условного оператора Если , то . Условие задачи не предполагает выполнение каких-либо действий при невыполнении условия. Заменяем слова ЕСЛИ, ТО на зарезервированные в Паскале слова, получим оператор сокращённого ветвления

If then .

Рассмотреть пример.

В случае, если у нас не один оператор, а серия операторов, то используются операторные скобки begin … end., заключающие в себя эту последовательность операторов.

1. Физкультминутка (2 минуты).

2. Закрепление изученного материала (10 минут).

Выполнение задания 4 — 6.

Задание 4.

Определить значение переменной А в результате выполнения фрагмента алгоритма, представленного блок-схемой.

1. Если А = 25, В = 5

Ответ____________ .

1. Если А = 25, В = 4

Ответ____________ .

Два правильных ответа – 2 балла, один правильный ответ – 1 балл.

Задание 5.

Построить график, описываемый алгоритмом. Если (X -2) и (XY:= X*X, иначе Y:=4.

Если справились полностью 2 балла.

Перед выполнением упражнения 6, выполнить упражнение на расслабление глаз.

Это упражнение ослабляет напряжение, расслабляет глазные нервы, а в некоторой степени успокаивает ум.
• Разогреваем руки, потерев одну ладонь о другую. Делаем это до тех пор, пока руки не станут теплыми. Теперь нужно облокотиться на стол перед собой, сложить пальцы обеих рук в два полушария и мягко прикрыть ими глаза. Почувствуйте, как приятны для глаз тепло и темнота. Можно усилить это чувство, сделав при этом пару глубоких вдохов. Представьте себе, что при вдохе наполняются не только легкие, но и глаза свежим кислородом, что делает их более свежими и сильными.

ГРУППА 1. Ввести с клавиатуры 2 числа. Вывести на экран их разность, вычитая из большего числа меньшее число.

Задание 6.

Работа в группе. Решение практических задач на языке программирования Pascal.

ГРУППА 2. Ввести с клавиатуры 2 числа. Вывести на экран их частное или сообщение «На ноль делить нельзя!»

Математическая модель + блок схема + программа = 3 балла. (каждому из группы).

1. Домашнее задание (1 минута)

2. Контроль усвоения ЗУН (3 минуты)

Перед выполнением итогового контроля, когда силы обучающихся уже истощены выполняются упражнения, которые позволяют поплнить энергию.

Источник энергии

Это классическое упражнение. Оно расслабляет затылочную и плечевую мускулатуру и улучшает дыхание. В головной мозг поступает много кислорода, за счет чего улучшается еще и слух и зрение.
• Положите руки на стол перед собой. Выдохните и позвольте своей голове медленно опуститься вниз. Почувствуйте, мускулы вашего затылка растянулись, полностью расслабьте плечи. Теперь снова медленно поднимите голову и при этом сделайте вдох. Дайте голове полностью откинуться назад, пока вам не покажется, что ваша грудная клетка распахнулась и наполнилась воздухом. Когда вы снова будете выдыхать, делайте это медленно и снова опустите голову вниз, пока подбородок вновь не ляжет на грудь. Подарите себе три таких особенных освежающих вдоха

Итоговый контроль усвоения знаний.

1. Алгоритм, в котором его выполнение определяется проверкой каких-либо условий, называется…

A. разветвляющимся

B. циклическим

C. следования

D. линейным

E. процедурным

2. Служебное слово IF в условном операторе переводится как…

A. если

B. то

C. иначе

D. ввод

E. условие

3. Служебное слово THEN в условном операторе переводится как…

A. если

B. то

C. иначе

D. ввод

E. условие

4. Служебное слово ELSE в условном операторе переводится как…

A. если

B. то

C. иначе

D. ввод

E. условие

5. Укажите правильный вариант использования условного оператора.

A. IF THEN begin end ELSE begin end;

B. IF THEN ; ELSE ;

C. THEN begin end IF ELSE begin end;

D. THEN ELSE IF ;

E. IF THEN

6. Укажите правильный вариант использования неполного ветвления.

A. IF THEN begin end;

B. THEN ; ELSE ;

C. IF ELSE begin end;

D. ELSE IF ;

E. THEN IF

Проверяется учителем. Результат на следующий урок.

1. Рефлексия (2 минуты).

2. Итоги урока (2 минуты).

3. Окончание урока (1 минута).

В течение всего урока, по окончании каждого этапа при помощи методики цветописи Лутошкина учащиеся оценивают свой эмоциональный настрой.

Этапы								трудно сказать
Орг. момент
Актуализация внимания и знаний
Проверка домашнего задания
Изучение нового материала.
Закрепление
Домашнее задание
Контроль усвоения ЗУН
Рефлексия
Итоги урока

Оценка – количественный показатель эмоциональной атмосферы.

Алгоритмизация и программирование

Алгоритмы, виды алгоритмов, описание алгоритмов. Формальное исполнение алгоритмов

Термин «алгоритм», впервые употребленный в современном значении. Лейбницем (1646–1716), является латинизированной формой имени великого персидского математика Мухаммеда бен Муссы аль-Хорезми (ок. 783 – ок. 850). Его книга «Об индийском счете» в XII в. была переведена на латинский язык и пользовалась широкой популярностью не одно столетие. Имя автора европейцы произносили как Алгоритми (Algorithmi), и со временем так стали называть в Европе всю систему десятичной арифметики.

Научное определение алгоритма дал А. Чёрч в 1930 году. В наше время понятие алгоритма является одним из основополагающих понятий вычислительной математики и информатики.

Алгоритм — это точное и полное описание последовательности действий над заданными объектами, позволяющее получить конечный результат.

Можно сказать, что алгоритм решения какой-либо задачи — это последовательность шагов реализации (или нахождения) этого решения, а процесс построения алгоритма (алгоритмизация) — разложение задачи на элементарные действия или операции.

Область математики, известная как теория алгоритмов, посвящена исследованию свойств, способов записи, области применения различных алгоритмов, а также созданию новых алгоритмов. Теория алгоритмов находит широкое применение в различных областях деятельности человека — в технике, производстве, медицине, образовании и т. д. Появление компьютера позволило решать чрезвычайно сложные, трудоемкие задачи.

Определение алгоритма для применения в области информатики нуждается в некотором уточнении. Во-первых, решение задач в информатике всегда связано с преобразованием информации, а значит, исходными данными и результатом работы алгоритма должна быть информация. Это может быть представлено в виде схемы.

Во-вторых, алгоритмы в информатике предназначены для реализации в виде компьютерных программ или для создания некоторой компьютерной технологии. Для выполнения алгоритма требуется конечный объем оперативной памяти и конечное время.

Основные требования, предъявляемые к алгоритмам:

Дискретность (прерывность): алгоритм должен представлять решение задачи в виде последовательности простых (или ранее определенных) этапов (шагов). Каждый шаг алгоритма формулируется в виде инструкций (команд).

Определенность (детерминированность; лат. determinate — определенность, точность): шаги (операции) алгоритма должны допускать однозначную трактовку и быть понятными для исполнителя алгоритма. Это свойство указывает на то, что любое действие в алгоритме должно быть строго определено и описано для каждого случая.

Массовость: алгоритм должен давать решение не только для конкретного набора значений, а для целого класса задач, который определяется диапазоном возможных исходных данных (область применимости алгоритма). Свойство массовости подразумевает использование переменных в качестве исходных данных алгоритма.

Результативность: алгоритм должен давать конкретный результат, т. е. должны быть рассмотрены все возможные ситуации и для каждой из них получен результат. Под результатом может пониматься и сообщение о том, что задача решения не имеет.

Конечность: количество шагов алгоритма должно быть конечным.

Эффективность: количество шагов и сами шаги алгоритма должны быть такими, чтобы решение могло быть найдено за конечное и, более того, приемлемое время.

Для оценки и сравнения алгоритмов существует много критериев. Чаще всего анализ алгоритма (или, как говорят, анализ сложности алгоритма) состоит в оценке временных затрат на решение задачи в зависимости от объема исходных данных. Используются также термины «временная сложность», «трудоемкость» алгоритма. Фактически эта оценка сводится к подсчету количества основных операций в алгоритме, поскольку каждая из них выполняется за заранее известное конечное время. Кроме временной сложности, должна оцениваться также емкостная сложность, т. е. увеличение затрат памяти в зависимости от размера исходных данных. Оценка сложности дает количественный критерий для сравнения алгоритмов, предназначенных для решения одной и той же задачи. Оптимальным (наилучшим) считается алгоритм, который невозможно значительно улучшить в плане временных и емкостных затрат.

Анализом сложности алгоритмов, исследованием классов задач, решаемых с помощью алгоритмов той или иной сложности, и многими другими теоретическими вопросами занимается специальная область информатики.

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов.

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур:

1. следование — образуется из последовательности действий, следующих одно за другим;
2. ветвление (развилка) — обеспечивает в зависимости от результатов проверки условия (ДА или НЕТ) выбор одного из альтернативных путей алгоритма;
3. цикл — обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.

Для описания алгоритмов наиболее распространены следующие методы (языки):

Обычный язык. Изложение алгоритма ведется на обычном языке с разделением на последовательные шаги.

Блок-схемы. Графическое изображение алгоритма с помощью специальных значков-блоков.

Формальные алгоритмические языки (языки программирования). При записи алгоритмов используют строго определенный набор символов и составленных из них специальных зарезервированных слов. Имеют строгие правила построения языковых конструкций.

Псевдокод. Синтез алгоритмического и обычного языков. Элементы некоторого базового алгоритмического языка используются для строгой записи базовых структур алгоритма.

Словесный способ (запись на обычном языке) не имеет широкого распространения, т. к. таких описаний есть ряд недостатков:

• строго не формализуемы;
• достаточно многословны;
• могут допускать неоднозначность толкования отдельных предписаний;
• сложные задачи с анализом условий, с повторяющимися действиями трудно представляются в словесной или словесно-формульной форме.

Графический способ представления информации является более наглядным и компактным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление алгоритма называется блок-схемой. Определенному типу действия (ввод/вывод данных, проверка условия, вычисление выражения, начало и конец алгоритма и т. п.) соответствует определенная геометрическая фигура — блочный символ. Блоки соединяются между собой линиями переходов, которые определяют очередность выполнения действий.

Название символа	Графическое изображение	Комментарии
Пуск/Останов (блоки начала и конца алгоритма)		Указание на начало или конец алгоритма
Ввод/Вывод данных (блоки ввода, вывода		Организация ввода/вывода в общем виде
Процесс (операторные блоки)		Выполнение вычислительного действия или последовательности действий (можно объединять в один блок), которые изменяют значение, форму представления или размещение данных
Условие (условный блок)		Выбор направления выполнения алгоритма. Если условие, записанное внутри ромба, выполняется, то управление передается по стрелке «да», в противном случае — по стрелке «нет». Таким образом, реализуется процесс изменения последовательности вычислений в зависимости от выполнения условия
Начало цикла с параметром		Используется для организации циклических конструкций с известным количеством итераций (повторений) и известным шагом изменения параметра цикла. Внутри блока для параметра цикла указываются через запятую его начальное значение, конечное значение и шаг изменения. Цикл, для которого неизвестно количество повторений, записывается с помощью условного и операторных блоков
Предопределенный процесс		Используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращения к библиотечным подпрограммам
Печать сообщений (документ)		Вывод результатов на печать

При составлении блок-схемы необходимо проверять выполнение следующих условий:

1. из каждого прямоугольника и параллелограмма (кроме конца алгоритма) должна выходить только одна стрелка;
2. в каждый прямоугольник и параллелограмм (кроме начала алгоритма) должна входить хотя бы одна стрелка;
3. в каждый ромб должна входить хотя бы одна стрелка, а выходить из него — две стрелки, помеченные словами «ДА» и «НЕТ».

Псевдокод занимает промежуточное положение между естественным языком и языками программирования. В псевдокоде не приняты строгие синтаксические правила для записи команд, что отличает формальные языки программирования. Однако в псевдокоде есть некоторые конструкции, которые присущи формальным языкам, что облегчает переход от записи алгоритма на псевдокоде к записи алгоритма на языке программирования. Псевдокоды бывают разные. Рассмотрим учебный (школьный) алгоритмический язык АЯ.

Алфавит учебного алгоритмического языка является открытым. В него могут быть введены любые понятные всем символы: русские и латинские буквы, знаки математических операций, знаки отношений, специальные знаки и т. д. Кроме алфавита, в алгоритмической нотации определяются служебные слова, которые являются неделимыми. Служебные слова обычно выделяются жирным шрифтом или подчеркиванием. К служебным словам относятся:

алг — заголовок алгоритма	нц — начало цикла	знач
нач — начало алгоритма	кц — конец цикла	и
кон — конец алгоритма	дано	или
арг — аргумент	надо	не
рез — результат	если	да
цел — целый	то	нет
сим — символьный	иначе	при
лит — литерный	всё	выбор
лог — логический	пока	утв
вещ — вещественный	для	ввод
таб — таблица	от	вывод
длин — длина	до

Общий вид записи алгоритма на псевдокоде:

алг — название алгоритма (аргументы и результаты)

дано — условие применимости алгоритма

надо — цель выполнения алгоритма

нач — описание промежуточных величин

последовательность команд (тело алгоритма)

кон

Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключенная между словами нач и кон, — телом алгоритма (исполняемой частью алгоритма).

В предложении алг после названия алгоритма в круглых скобках указываются характеристики (арг, рез) и тип значения (цел, вещ, сим, лит или лог) всех входных (аргументы) и выходных (результаты) переменных. При описании массивов (таблиц) используется служебное слово таб, дополненное именем массива и граничными парами по каждому индексу элементов массива.

Команды учебного языка:

1. Оператор присваивания, который обозначается «:=» и служит для вычисления выражений, стоящих справа, и присваивания их значений переменным, указанным в левой части. Например, если переменная а имела значение 5, то после выполнения оператора присваивания а := а + 1, значение переменной а изменится на 6.

2. Операторы ввода/вывода:

ввод (список имен переменных)

вывод (список вывода)

Список вывода может содержать комментарии, которые заключаются в кавычки.

3. Оператор ветвления (с использованием команды если…то… иначе…всё; выбор);

4. Операторы цикла (с использованием команд для, пока, до).

Запись алгоритма на псевдокоде:

Здесь в предложениях дано и надо после знака «|» записаны комментарии. Комментарии можно помещать в конце любой строки, они существенно облегчают понимание алгоритма.

При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается произвольное изображение команд. Вместе с тем такая запись позволяет понять человеку суть дела и исполнить алгоритм. Однако алгоритм, предназначенный для исполнения на компьютере, должен быть записан на строго формализованном языке. Такой язык называется языком программирования, а запись алгоритма на этом языке — компьютерной программой.

Для решения одной и той же задачи можно предложить несколько алгоритмов. Алгоритмы составляются с ориентацией на определенного исполнителя алгоритма. У каждого исполнителя имеется свой конечный набор команд, которые для него понятны и исполняемы. Этот набор называется системой команд исполнителя. Пользуясь системой команд, исполнитель может выполнить алгоритм формально, не вникая в содержание поставленной задачи. От исполнителя требуется только строгое выполнение последовательности действий, предусмотренной алгоритмом. Таким образом, в общем случае алгоритм претерпевает изменения по стадиям:

• первая стадия — алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает;
• вторая стадия — алгоритм должен быть представлен в форме, понятной исполнителю алгоритма (вторая стадия может отсутствовать, если исполнять алгоритм будет сам разработчик).

Примеры решения задач

Пример 1. Исполнитель Утроитель может выполнить только две команды, которым присвоены номера:

1 — вычти 1;

3 — умножь на 3.

Первая команда уменьшает число на 1, вторая — увеличивает его втрое.

Написать набор команд (не более пяти) получения из числа 3 числа 16. В ответе указать только номера команд.

Решение.

1 (3 – 1 = 2)

3 (2 * 3 = 6)

3 (6 * 3 = 18)

1 (18 – 1 = 17)

1 (17 – 1 = 16)

Ответ: 13311

Пример 2. Имеется Исполнитель алгоритма, который может передвигаться по числовой оси.

Система команд Исполнителя алгоритма:

1. «Вперед N» (Исполнитель алгоритма делает шаг вперед на N единиц).

2. «Назад M» (Исполнитель алгоритма делает шаг назад на M единиц).

Переменные N и M могут принимать любые целые положительные значения. Известно, что Исполнитель алгоритма выполнил программу из 50 команд, в которой команд «Назад 2» на 12 больше, чем команд «Вперед 3». Других команд в программе не было. Какой одной командой можно заменить эту программу, чтобы Исполнитель алгоритма оказался в той же точке, что и после выполнения программы?

Решение.

1. Найдем, сколько было команд «Вперед», а сколько «Назад». Учитывая, что общее количество команд равно 50 и что команд «Назад» на 12 больше, чем команд «Вперед». Получим уравнение: x + (x + 12) = 50, где x — количество команд «Вперед». Тогда общее количество команд «Вперед»: x = 19, а количество команд «Назад»: 19 + 12 = 31.

2. Будем вести отсчет от начала числовой оси. Выполнив 19 раз команду «Вперед 3», Исполнитель алгоритма оказался бы на отметке числовой оси 57 (19 * 3 = 57). После выполнения 31 раз команды «Назад 2» (31 * 2 = 62) он оказался бы на отметке –5 (57 – 62 = –5).

3. Все эти команды можно заменить одной — «Назад 5».

Ответ: команда«Назад 5».

Пример 3. Черепашка является исполнителем для создания графических объектов на рабочем поле. При движении Черепашка оставляет след в виде линии. Черепашка может исполнять следующие команды:

Название команды	Параметр	Действия исполнителя
вп	Число шагов	Продвигается в направлении головы на указанное число шагов
нд	Число шагов	Продвигается в направлении, противоположном направлению головы на указанное число шагов
пр	Число градусов	Поворачивается направо относительно направления, заданного головой черепашки
лв	Число градусов	Поворачивается налево относительно направления, заданного головой черепашки

Для записи повторяющихся действий (цикла) используется команда Повтори. В этой команде два параметра: первый задает количество повторений (итераций), а второй — список команд которые должны повторяться (тело цикла); список заключается в квадратные скобки.

Записать для исполнителя Черепашка алгоритмы:

а) построения квадрата со стороной 100;

б) построения правильного шестиугольника со стороной 50.

в) построения изображения цифры 4, если голова Черепашки смотрит на север.

Ответ: а) Повтори 4 [вп 100 пр 90]; б) Повтори 6 [вп 50 пр 360/6]; в) вп 100; повтори [лв 135 вп 50].

Пример 4. Два игрока играют в следующую игру (это вариант восточной игры). Перед ними лежат три кучки камней, в первой из которых 2, во второй — 3, в третьей — 4 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или удваивает число камней в одной из кучек, или добавляет по два камня в каждую из них. Выигрывает игрок, после хода которого либо в одной из кучек становится не менее 15 камней, либо общее число камней в трех кучках становится не менее 25. Кто выиграет при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ следует обосновать.

Решение. Удобнее всего составить таблицу возможных ходов обоих игроков. Заметим, что в каждом случае возможны всего четыре варианта хода. В таблице курсивом выделены случаи, которые сразу же приносят поражение игроку, делающему этот ход (например, когда камней в какой-либо кучке становится больше или равно 8, другой игрок непременно выигрывает следующим ходом, удваивая количество камней в этой кучке). Из таблицы видно, что при безошибочной игре обоих игроков первый всегда выиграет, если первым ходом сделает 4, 5, 6. У второго игрока в этом случае все ходы проигрышные.

	1-й ход	2-й ход
Начало	1-й игрок	2-й игрок	1-й игрок	2-й игрок
2,3,4	4,3,4	8,3,4	выигрыш
4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
4,3,8	выигрыш
6,5,6	12,5,6	выигрыш
6,10,6	выигрыш
6,5,12	выигрыш
8,7,8	выигрыш
	2,6,4	4,6,4	8,6,4	выигрыш
4,12,4	выигрыш
4,6,8	выигрыш
6,8,6	выигрыш
2,12,4	выигрыш
2,6,8	выигрыш
4,8,6	выигрыш
2,3,8	выигрыш
4,5,6	8,5,6	выигрыш
4,10,6	выигрыш
4,5,12	выигрыш
6,7,8	выигрыш

Пример 5. Записано 7 строк, каждая из которых имеет свой номер. В нулевой строке после номера записана цифра 001. Каждая последующая строка содержит два повторения предыдущей строки и добавленной в конец большой буквы латинского алфавита (первая строка — A, вторая строка — B и т. д.). Ниже приведены первые три строкиєтой записи (в скобках указан номер строки):

(0) 001

(1) 001001A

(2) 001001A001001AB

Какой символ находится в последней строке на 250-м месте (считая слева направо)?

Примечание. Первые семь букв латинского алфавита: A, B, C, D, E, F, G.

Решение. Найдем длину каждой строки. Длина каждой следующей строки в два раза больше длины предыдущей плюс один символ, длина строк составит:

(0) 3 символа;

(1) 3*2+1=7;

(2) 7*2+1=15;

(3) 15*2+1=31;

(4) 31*2+1=63;

(5) 63*2+1=127;

(6) 127*2+1=255 символов.

Так как задано 7 строк, а нумерация начинается с нулевой строки, последняя строка имеет номер 6 и содержит 255 символов. Последний символ в строке — F. Предпоследний элемент — E, далее идут символы D, C, B, A, 1 (по правилу формирования строк). Таким образом, 250-й символ — это 1.

Ответ: 1.

Пример 6. Имеется фрагмент алгоритма, записанный на учебном алгоритмическом языке:

n := Длина(а)

k = 2

b := Извлечь(а, k)

нц для i от 7 до n – 1

с := Извлечь(а, i)

b := Склеить(b, с)

кц

Здесь переменные а, b, с — строкового типа; переменные n, i — целые.

В алгоритме используются следующие функции:

Длина(х) — возвращает количество символов в строке х. Имеет тип «целое».

Извлечь(х, i) — возвращает i-й символ слева в строке х. Имеет строковый тип.

Склеить(х, у) — возвращает строку, в которой находятся все символы строки х, а затем все символы строки у. Имеет строковый тип.

Какое значение примет переменная b после выполнения этого фрагмента алгоритма, если переменная а имела значение «ВОСКРЕСЕНЬЕ»?

Решение. Находим общее число символов в строке а, получим, что n = 11.

Выполняя команду b := Извлечь(а, k) при k = 2, получим, что b примет значение «О«.

В цикле последовательно, начиная с 7-го символа строки а и заканчивая предпоследним (n – 1), извлекаем символ из строки а и присоединяем к строке b.

В результате получим слово «ОСЕНЬ» (символы с номерами 2 + 7 + 8 + 9 + 10).

Ответ: «ОСЕНЬ«

Пример 7. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Числовой ряд, который называется его именем, получился в результате решения задачи о кроликах, которую Фибоначчи изложил в своей «Книге Абака», написанной в 1202 году. Он выглядит так:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…

В этом ряду каждое следующее число, начиная с третьего, равно сумме двух предыдущих. Составить словесный алгоритм и блок-схему проверки принадлежности введенного числа n ряду Фибоначчи.

Решение. Словесный алгоритм:

1. Ввести число n.
2. Установить значение первых трех чисел Фибоначчи: 1, 1, 2 (сумма двух предыдущих чисел).
3. Пока введенное число n больше очередного числа Фибоначчи, взять два последних числа Фибоначчи и получить из них новое число Фибоначчи.
4. Если число Фибоначчи равно введенному n или было введено число n = 1, значит, что было введено число Фибоначчи, в противном случае — введенное число не является числом Фибоначчи.

Приведенный словесный алгоритм в пункте 1, 2 содержит начальные установки, в пункте 3 — цикл с условием, а пункт 4 — это вывод результата работы алгоритма.

Блок-схема алгоритма:

Обозначения:

F — текущее число ряда Фибоначчи;

F1 и F2 — два предыдущих числа ряда Фибоначчи для числа F;

n — число, для которого требуется определить, является ли оно числом из ряда Фибоначчи.

Использование основных алгоритмических конструкций: следование, ветвление, цикл

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.

Базовая структура СЛЕДОВАНИЕ указывает на то, что управление передается последовательно от одного действия к другому.

Учебный алгоритмический язык	Язык блок-схем
действие 1 действие 2 … действие n

Использование исключительно этой структуры возможно лишь для достаточно простых задач, ход решения которых не меняется в зависимости от конкретных исходных данных и состоит в последовательном выполнении определенных операций.

В качестве примера рассмотрим решение простой задачи.

Пример. Найти y(x) = x2 + 3x + 5, используя только операции умножения и сложения.

Решение. На рис. приводятся два алгоритма, реализующие решение поставленной задачи.

Порядок вычисления y(x) в первом случае — обычный, а во втором — (x + 3) x + 5. Обе формулы эквивалентны, но в первом случае для вычисления необходимо 2 умножения, 2 сложения и 3 переменных (x, y, z), а во втором используются 1 умножение, 2 сложения и 2 переменные (x, y).

Приведенный пример показывает, что даже простые задачи могут решаться с помощью различных вариантов алгоритмов.

Обратите внимание, как в блоке следования используется оператор присваивания.

Операция присваивания — важнейшая операция во всех языках программирования. С помощью присваивания переменные получают новые значения: в левой части инструкции ставится идентификатор величины, а в правой части — выражение, значение которого можно определить.

В операторах присваивания используется либо привычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных правой части уже определены.

Базовая структура ВЕТВЛЕНИЕ (РАЗВИЛКА) используется в случае, когда выполнение программы может измениться в зависимости от результата проверки условия и пойти двумя разными (альтернативными) путями. Другими словами, условие является некоторым высказыванием (предикатом) и может быть истинным или ложным (принимать значение TRUE или FALSE). Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.

Различают две структуры этого типа — полную и неполную. В случае полной структуры, если условие выполняется (является истинным), вслед за ним выполняется действие 1, иначе — действие 2. В случае неполной структуры, если условие выполняется (является истинным), то вслед за ним выполняется действие 1, иначе ничего не происходит.

Важную роль в операторах ветвления играют содержащиеся в них условия. В простейшем случае условиями служат отношения между величинами. Условия с одним отношением называют простыми условными выражениями, или простыми условиями. В некоторых задачах необходимы более сложные условия, состоящие из нескольких простых, например условие А < X < С, т. е. Х < А и (Х > C) (возможна запись (Х < А) and (Х > C)). Объединение нескольких простых условий в одно образует составное условное выражение, или составное условие. Составные условия образуются с помощью логических операторов not (отрицание), and (логическое И), or (логическое ИЛИ), хоr (исключающее ИЛИ).

Структура ВЕТВЛЕНИЕ существует в четырех основных вариантах:

если — то (неполная структура);

если — то — иначе (полная структура);

выбор (неполный);

выбор — иначе (полный).

Учебный алгоритмический язык	Язык блок-схем
1) если — то
если условие то действие 1 всё
2) если — то — иначе
если условие то действие 1 иначедействие 2 всё
3) выбор
выбор при условие 1: действие 1 при условии 2: действие 2 … при условие N: действие N всё
4) выбор — иначе
выбор при условие 1: действие 1 при условие 2: действие 2 … при условие N: действие N + 1 иначе действия N + 1 всё

В качестве простого примера рассмотрим нахождение модуля числа y(x) = |x|. Решение приведено на рис. для случаев полной (а) и неполной (б) структур ветвления.

Базовая структура ЦИКЛ служит для записи алгоритмов, в которых некоторая часть алгоритма (тело цикла) должна повторяться несколько раз. Количество повторений цикла может определяться разными способами, в зависимости от которых различают три вида циклов.

1. Цикл с предусловием, или цикл «пока». При реализации этого цикла сначала проверяется условие его выполнения. Пока оно выполняется, будут происходить повторения тела цикла. Отсюда и другое его название — цикл «пока». Если условие не выполняется при первой проверке, то тело цикла не будет выполняться вообще. После выхода из цикла управление передается следующей структуре. Для того чтобы избежать зацикливания, т. е. бесконечного цикла, в теле цикла обязательно должны изменяться параметры, записанные в условии.

Учебный алгоритмический язык	Язык блок-схем
нц пока условие тело цикла (последовательность действий) кц

2. Цикл с параметром. Этот вид цикла удобно использовать в тех случаях, когда заранее извесно количество повторений цикла. Вводится понятие счетчика цикла, который по умолчанию считается равным либо 1, либо –1. В некоторых случаях изменение счетчика цикла (приращение) указывают явно. Для организации цикла необходимо задать верхнюю и нижнюю границы изменения счетчика цикла. В зависимости от значения верхней и нижней границы определяется шаг цикла (1 или −1), т. е. значение счетчика цикла.

Учебный алгоритмический язык	Язык блок-схем
нц для i от i1 до i2 тело цикла (последовательность действий) кц

3. Цикл с постусловием, или цикл «до». При реализации этого цикла условие завершение цикла проверяется после тела цикла. В этом случае тело цикла всегда выполняется хотя бы один раз. Цикл будет выполняться до выполнения условия, отсюда и другое название — цикл «до». А пока условие не выполнено, будет повторяться тело цикла (выполнение условия, таким образом, является условием окончания цикла). В этом случае, как и в цикле «пока», необходимо предусмотреть в теле цикла изменение параметров условия цикла.

Учебный алгоритмический язык	Язык блок-схем
нц тело цикла (последовательность действий) до условие кц

Для всех видов цикла предусмотрена возможность досрочного выхода, т. е. прерывание работы цикла.

Помимо трех рассмотренных видов цикла существует и так называемый интерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия. На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата. Классический пример — вычисление суммы ряда с заданной точностью.

Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное условие выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т. е. не будет выполняться основное свойство алгоритма — результативность.

Пример. Вычислить сумму знакопеременного ряда $S=x-{x^2}/{2}+{x^3}/{3}-{x^4}/{4}+…$ с заданной точностью $ε$.

Для данной знакочередующейся бесконечной суммы требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше $ε$.

Решение. Запишем блок-схему алгоритма, где будем использовать следующие обозначения:

$S$ — частичная сумма ряда (стартовое значение равно 0);

$ε$ — точность вычисления;

$i$ — номер очередного слагаемого;

$m$ — значение очередного слагаемого;

$p$ — числитель очередного слагаемого.

На псевдокоде алгоритм можно записать следующим образом:

Примечание. Следует отметить, что ряд будет сходящимся только при выполнении условия 0 < х < 1.

Возможны случаи, когда внутри тела цикла необходимо повторить некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле, или вложенного цикла. Глубина вложения циклов (количество вложенных друг в друга циклов) может быть различной.

При использовании такой структуры для экономии времени выполнения необходимо выносить из внутреннего цикла во внешний все действия, результаты которых не зависят от параметра внутреннего цикла.

Пример. Вычислить сумму элементов для заданной матрицы (таблицы из 5 строк и 3 столбцов) А(5,3).

Решение. Алгоритм решения задачи на псевдокоде:

Основная часть блок-схемы нахождения суммы элементов матрицы будет иметь следующий вид:

Здесь порядок выполнения вложенных циклов следующий: счетчик внутреннего цикла изменяется быстрее, т. е. для i = 1(внешний цикл), j пробегает значения 1, 2, 3 (внутренний цикл); далее i = 2, j опять пробегает значения 1, 2, 3 и т. д.

Примеры решения задач

Пример 1. Дан фрагмент блок-схемы некоторого алгоритма.

Определить значение переменной А после выполнения фрагмента алгоритма.

Какие исправления нужно внести, чтобы изменение значения переменной А происходило в обратном порядке?

Как записать исходный алгоритм с помощью двух других видов цикла?

Решение. Если представить пошаговое выполнение алгоритма в виде таблицы, получим:

Начальные установки:	A = 100000; N = 2
1-я итерация	A = 10000; N = 4
2-я итерация	A = 1000; N = 6
3-я итерация	A = 100; N = 8
4-я итерация	A = 10; N = 10
5-я итерация, выполнилось условие выхода: N > 10	Ответ: А = 1; N = 12

Таблица обратного хода изменения значения А будет иметь такой вид:

Начальные установки:	A = 1; N = 2
1-я итерация	A = 10; N = 4
2-я итерация	A = 100; N = 6
3-я итерация	A = 1000; N = 8
4-я итерация	A = 10000; N = 10
5-я итерация, выполнилось условие выхода: N > 10	А = 100000; N = 12

Блок-схема алгоритма примет такой вид:

В алгоритме нужно изменить начальное значение А и операцию деления заменить операцией умножения. Счетчик N в данном случае изменять не нужно.

В приведенной в условии блок-схеме используется цикл с предусловием. Для цикла с параметром блок-схема алгоритма будет иметь такой вид:

Понятно, что цикл должен выполниться пять раз. В заголовке цикла необходимо указать начальное и конечное значение счетчика цикла N (приращение по умолчанию равно 1).

Для цикла с постусловием блок-схема исходного алгоритма имеет такой вид:

В данной схеме условие завершения цикла находится после тела цикла. Цикл, в отличие от цикла с предусловием, выполняется, пока значение условия ложно.

Пример 2. Сколько раз выполнится тело цикла в программе?

Q := 27; P := 36

нц пока (div(Q, 5) = div(P, 7))

Q := Q + 2

P := P + 3

кц

Примечание. Результат функции div(X, Y) — целая часть от деления X на Y.

Решение. Рассмотрим пошаговое выполнение алгоритма, оформив его в виде таблицы.

Начальные установки	Q := 27; P := 36
Проверка выполнения условия	div(27, 5) = 5; div(36, 7) = 5; 5 = 5
1-я итерация; выполнение тела цикла	Q := 29; P := 39
Проверка выполнения условия	div(29, 5) = 5; div(39, 7) = 5; 5 = 5
2-я итерация; выполнение тела цикла	Q := 31; P := 42
Проверка выполнения условия	div(31, 5) = 6; div(42, 7) = 6; 6 = 6
3-я итерация; выполнение тела цикла	Q := 33; P := 45
Проверка выполнения условия	div(33, 5) = 6; div(45, 7) = 6 6 = 6
4-я итерация; выполнение тела цикла	Q := 35; P := 48
Проверка выполнения условия. Условие не выполняется, цикл завершает работу	div(35, 5) = 7; div(48, 7) = 6; 7 ≠ 6

Ответ: цикл выполнится 4 раза.

Использование переменных. Объявление переменной (тип, имя, значение).
Локальные и глобальные переменные

Величины служат для описания объектов и процессов в материальном мире. Каждая величина имеет некоторые характеристики. В программировании понятие величины несколько отличается от понятия величины в естественных науках — оно является более формальным. Величиной называют объект — переменную, с которым связывается определенное множество значений. Такому объекту присваивается имя — идентификатор. Понятие переменной в программировании сходно с понятием переменной в математике. Например, в алгебраическом равенстве C = F + 2B – 5 значение переменной С зависит от значений переменных F и B, указанных в правой части равенства. Например, при F = 2 и B = 6, С = 9. Такое же равенство можно записать в программе, например на языке программирования Бейсик: C = F + 2*B – 5. В терминах языка программирования C, F и B — это идентификаторы (имена) переменных.

Переменная — это объект программы, имеющий имя и изменяемое значение. Для хранения переменной в памяти компьютера выделено определенное место.

Переменные величины в отличие от постоянных величин (констант) могут со временем менять свое значение. Константой называется величина, которая в ходе выполнения программы не меняет своего значения.

Назначение программы состоит в обработке информации, при этом, конечно, основную роль играют переменные.

Переменная характеризуется:

• идентификатором;
• типом;
• значением.

Каждая переменная имеет свой идентификатор, т. е. свое уникальное имя. Имя переменной показывает, в каком месте памяти компьютера она хранится, значение переменной считывается из указанного ее именем места в памяти. Двух переменных с одним именем в одном программном модуле (блоке) быть не должно. Примерами идентификаторов величин могут быть, например, следующие последовательности символов: a1, SUMMA, X_1, Y_1, My_program.

Во многих языках программирования существуют некоторые ограничения на задания имен переменных. Имена составляются из букв и цифр; первой литерой должна быть буква. Знак подчеркивания «_» считается буквой, его удобно использовать, чтобы улучшить восприятие длинных имен переменных. Разумно давать переменным логически осмысленные имена, в соответствии с их назначением. Нельзя использовать в качестве имен зарезервированные (служебные) слова языка программирования.

Тип переменной — это диапазон (набор) всех значений, которые может принимать данная переменная. Тип переменной определяет, какие операции для нее допустимы. Другими словами, тип переменной — это характеристика, которая для величины определяет:

• необходимый размер памяти;
• диапазон значений, которые может принимать величина;
• возможные операции над величиной (подразумеваются действия относительно использования величин в выражениях);
• формы представления величин (или формат представления величин).

Стандартные типы — это числовые, литерные и логические типы.

Числовой тип, к которому относятся целые и вещественные величины, позволяет оперировать с числами. Целые числа, которые в учебном алгоритмическом языке составляют тип цел, сверху ограничены положительным числом N_max, а снизу — отрицательным числом N_min. Значения N_max и N_min определяются объемом ячеек памяти, в которые записываются целые числа. Обычно для целых чисел выделяется два байта памяти, соответственно границы диапазона равны [N_min = –32768 и N_max = 32767]. Считается, что все операции с величинами типа цел выполняются по обычным правилам арифметики, за одним исключением: возможны две операции деления div и mod.

Операция div обозначает целочисленное деление. При делении с точностью до целых чисел получается два результата — частное и остаток. Знак результата берется по обычным правилам, а полученный остаток игнорируется. Например:

23 div 5 = 4;

2 div 6 = 0;

(–13) div 5 = –2;

(–13) div (–5) = 2.

Операция mod определяет остаток при делении двух целых чисел.

Например:

23 mod 5 = 3;

2 mod 6 = 2;

(–13) mod 5 = –3;

(–13) mod (–5) = 3;

8 mod 2 = 0.

Целые числа чаще всего используются в простых арифметических выражениях и выступают в программах в качестве различных счетчиков и значений индексов.

К другому числовому типу относятся вещественные (вещ) величины. Значения вещественных величин могут изображаться в форме с фиксированной запятой (например, 0,3333; 2,0; –4,567 и т. д.) и с плавающей запятой (например, 7,0*10², 5,173*10^–3 и т. д.).

В отличие от целых чисел, действия с вещественными числами могут быть неточными — это связано с ошибками округлений. Объем памяти, который предоставляется для хранения значений вещественной переменной, — от 4 до 10 байтов (в зависимости от выбранного формата числа). Над числовыми величинами можно выполнять как арифметические операции, так и операции сравнения (>, <, >=, <=, =, ).

Литерный тип, включающий символы и строки, дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов: букв, цифр, знаков препинания, пробела и других специальных знаков (возможными символами могут быть символы таблицы ASCII). Литерные величины обычно заключаются в кавычки: «а», «В», «СТРОКА», «1_2_3». В учебном алгоритмическом языке литерные величины обозначаются как лит. В других языках программирования (например, в Паскале) различают символьный (char) и строковый (string) типы. Величины символьного типа состоят из одного символа и занимают в памяти всего 1 байт. Величины строкового типа представляют собой различные последовательности символов, которые предусмотрены кодовой страницей, установленной в компьютере. Длина строки может составлять от 0 до 255 символов. Над всеми литерными величинами возможны операции сравнения. С помощью отношений типа «a» < «b», «b» < «c», «c» < «d»,… выполняется упорядочение литерных величин (сортировка по возрастанию или убыванию).

Еще одной операцией, характерной для символьных и строковых величин, является операция конкатенации (слияния): «a» + «b» = «ab».

Логический тип позволяет определять логические переменные, которые могут принимать только два значения: истина (true) или ложь (false). Для представления логической величины достаточно одного бита, однако, поскольку место в памяти выделяется по байтам, логической величине отводится минимальная «порция» памяти — один байт. Над логическими величинами можно выполнять все стандартные логические операции.

Значение — это непосредственно то, чему равна переменная в конкретный момент времени. Это может быть число, символ, текст и т. д. Значение переменной в программе можно задать двумя способами: присваиванием и с помощью процедуры ввода.

Оператор присваивания

Во всех языках программирования оператор присваивания является одним из важнейших. С помощью присваивания переменные получают новые значения, например:

Д := 13;

D1 := C;

Х := Х + 1.

В операторах присваивания используется либо обычный знак равенства, либо сочетание двоеточия и знака равенства «:=». Поскольку знак присваивания — это не знак равенства, возможны записи вида Х := Х + 1 или А := А – В. Нужно учитывать, что оператор присваивания будет выполняться только в том случае, если значения всех переменных в правой части уже определены и выполняется соответствие типов для правой и левой части оператора присваивания. Например, С := А > B выполнится только в том случае, если для переменной С определен булевский (логический) тип. Операция присваивания может быть применена к большинству типов величин. Однако для каждого из типов предусмотрен свой набор операций.

Локальные, глобальные и общие переменные

Каждая переменная характеризуется областью действия или областью видимости. По зоне видимости в языках программирования различают локальные и глобальные переменные. Первые доступны только конкретному подалгоритму (вспомогательному алгоритму, подпрограмме, модулю), вторые — всему алгоритму (программе). С распространением модульного и объектного программирования появились еще и общие переменные, доступные для определенных уровней иерархии подпрограмм.

Ограничение зоны видимости придумали как для возможности использовать одинаковые имена переменных, так и для защиты от ошибок, связанных с неправомерным использованием переменных.

Имена локальных и глобальных переменных могут совпадать. При этом действует правило: локальные переменные на время работы подпрограмм, в которых они объявлены, экранируют, т. е. перекрывают глобальные переменные. Например, если в основной программе переменная с именем с определена как логическая, а в подпрограмме идентификатор с используется для задания вещественной переменной, то только на время работы подпрограммы с можно использовать как число — в остальных случаях идентификатор с определяет логическую переменную.

Примеры решения задач

Пример 1. Значения заданных переменных А, В перераспределить таким образом, чтобы А и В поменялись значениями.

Решение. Возможны два варианта решения:

С использованием промежуточной переменной С	Без использования дополнительной переменной
C := A; A := B; B := C	A := A + B; B := A – B; A := A – B

Пример 2. Определить значение переменной A после выполнения фрагмента алгоритма:

Решение. Оформим решение в виде таблицы.

A	B	D	Условие
2	–2	10	да
–4	–2	12	да
8	–2	14	да
–16	–2	16	да
32	–2	18	да
–64	–2	20	да
128	–2	22	нет — окончание цикла

Ответ: А = 128.

Пример 3. Определить значение переменной S:

A := –1; B := 1

нц пока A + B < 10

A := A + 1; B := B + A

кц

S := A * B

Решение. Оформим решение в виде таблицы.

A	B	A + B	S
–1	1	0
0	1	1
1	2	3
2	4	6
3	7	10 — условие выхода из цикла	21

Ответ: S = 21.

Пример 4. Записать последовательность операций присваивания (:=), которая позволит определить номера подъезда и этажа по номеру N квартиры девятиэтажного дома, считая, что на каждом этаже по 4 квартиры, а нумерация квартир начинается с первого подъезда.

Решение.

4 * 9 = 36 {количество квартир в подъезде}

Х := (N – 1) div 36 + 1 {номер подъезда}

N := N – (X – 1) * 36 { N ∊[1, 36] }

Y := (N – 1) div 4 + 1 {номер этажа}

Например, для квартиры с номером 150 получим:

Х = (150 – 1) div 36 + 1 = 4 + 1 = 5;

N = 150 – (5 – 1) * 36 = 6;

Y = (6 – 1) div 4 + 1 = 2.

Ответ: квартира с номером 150 находится в пятом подъезде, на втором этаже.

Работа с массивами (заполнение, считывание, поиск, сортировка, массовые операции и др.)

Величины числового, литерного, логического типов представляются одним значением и относятся к простым типам данных. Характерной особенностью простых типов является атомарность, т. е. они не могут вмещать элементы других типов. Типы данных, которые не удовлетворяют данному условию, называются структурированными, или составными. Например, массивы, записи, строки, множества, файлы. Структурированный тип характеризуется множеством элементов, из которых складываются данные этого типа. Элементы структурированного типа называются компонентами. В свою очередь компонента структурированного типа может принадлежать также к структурированному типу. Из простых данных сложные структуры могут получаться двумя способами:

1. объединением однородных элементов данных;
2. объединением разнородных элементов данных.

В первом случае примером могут служить массивы, а во втором — записи.

Информацию удобно представлять в виде таблиц. Наиболее привычными являются прямоугольные таблицы, т. е. таблицы, состоящие из строк и столбцов. В том числе таблицы, состоящие из единственной строки или единственного столбца, — линейные таблицы, имеющие одно «измерение».

Табличные величины относятся к составным величинам, т. к. включают в себя другие величины. В учебном алгоритмическом языке табличный тип обозначается как таб. Таблицы в программировании принято называть массивами. В математике прототипом массивов являются матрицы и векторы.

Массив

Массив — это упорядоченный набор данных, имеющий одно имя и состоящий из фиксированного числа однотипных элементов.

Каждый элемент массива снабжен индексом. Индекс — это порядковый номер элемента, определяющий его положение в массиве. Таким образом, элементы массива идентифицируются с помощью имени массива и с помощью своих индексов.

Количество элементов массива называется размерностью массива.

Итак, массив характеризуется:

• размерностью;
• базовым типом элементов;
• типом индекса (может быть только порядковым типом);
• множеством значений для индекса.

Массив может быть одномерным (вектор) и многомерным (матрица).

Одномерный массив содержит одно измерение; каждый элемент массива обозначается идентификатором (именем) массива с индексом. Многомерный массив содержит n-е количество измерений; каждый элемент массива обозначается идентификатором массива для n индексов.

Существует несколько способов заполнения массива данными:

1. непосредственное присваивание значений элементам;
2. заполнение массива произвольными элементами, случайными числами;
3. ввод значений элементов с клавиатуры или чтение из файла.

Необходимо заметить, что заполнение массива происходит поэлементно. Для этого используют оператор цикла. Вывод массива также осуществляется поэлементно с помощью оператора цикла.

Примечание. Строковый тип данных напоминает одномерный массив, в котором элементами являются символы. К примеру, строку «МАМА КУПИЛА ХЛЕБ» можно рассматривать как одномерный массив из 16 символов (включая пробелы). Эту строку можно обозначить идентификатором (например, Novost) и пронумеровать все символы, считая их элементами массива: Novost (l)  = «М», … Novost (16) = «Б».

Однако для работы с символьной информацией более гибким инструментом является не одномерный массив, а строка (string). Это связано с тем, что количество символов в строке, в отличие от массива, не фиксировано. Благодаря этому к строке можно без ограничений применять стандартные операции и функции, предназначенные для работы с текстом.

Задачи, связанные с обработкой массивов, как и все задачи вообще, условно можно разделить на два вида:

1. стандартные задачи;
2. задачи, решение которых требует знания вспомогательных алгоритмов, специальных методов и приемов.

Очевидно, что без умения решать задачи первых двух видов невозможно решать нестандартные задачи.

Стандартные задачи обработки массивов

Пример 1. В массиве А каждый элемент равен 0 или 1. Заменить все нули единицами и наоборот.

Решение. Достаточно одного оператора присваивания в теле цикла:

A[i] := 1 – A[i].

Пример 2. В массиве каждый элемент равен 0, 1 или 2. Переставить элементы массива так, чтобы сначала располагались все 0, затем все 1 и, наконец, все 2. Дополнительный массив не использовать.

Решение. Можно не переставлять элементы массива, а подсчитать количество 0, 1, 2 и заново заполнить массив требуемым образом.

Пример 3. Даны два n-элементных массива Х и Y одного типа. Поменять местами все X_i и Y_i, (i = 1…n), не используя промежуточные величины.

Решение. Обмен можно выполнить в цикле для всех i от 1 до n с помощью серии из трех операторов присваивания:

X[i] := X[i] + Y[i]

Y[i] := X[i] – Y[i]

X[i] := X[i] – Y[i].

Пример 4. Записать алгоритм нахождения максимального элемента массива А(n) и его номера.

Решение. На псевдокоде требуемый алгоритм запишется следующим образом:

Примечание. Если таких элементов несколько, будет найден номер последнего.

Пример 5. Найти сумму элементов одномерного массива А(n).

Решение. На псевдокоде алгоритм нахождения суммы запишется следующим образом:

Примечание. Для нахождения суммы положительных элементов массива вместо оператора

S := S + A[i] необходимо записать:

если A[i] > 0

то S := S + A[i]

всё

Пример 6. Записать алгоритм вычисления произведения элементов столбцов заданной вещественной двумерной матрицы A(n, m).

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 7. Подсчитать количество элементов для заданной целочисленной матрицы A(n, m), равных ее максимальному элементу.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 8. Запиcать алгоритм обмена элементами строк с номерами P и Q в заданной вещественной матрице A(n, m).

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 9. Включить заданное число D в одномерный упорядоченный по возрастанию массив F(n) с сохранением упорядоченности.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 10. Сформировать новый массив B из элементов целочисленного массива A(n), для которых выполняется условие D < A_i < C.

Решение. На псевдокоде алгоритм запишется следующим образом:

Пример 11. Найти в заданном целочисленном массиве А(m) хотя бы одну пару элементов, совпадающих по значению.

Решение. На псевдокоде алгоритм запишется следующим образом:

Поиск — одна из важных невычислительных задач. Проведение поиска в упорядоченном и неупорядоченном массивах отличается. В неупорядоченном массиве, если нет никакой дополнительной информации об элементе поиска, его выполняют с помощью последовательного просмотра всего массива. Такой поиск называют линейным. В любом случае существуют два условия окончания поиска:

1. элемент найден;
2. весь массив просмотрен — элемент не найден.

В упорядоченном массиве поиск можно значительно ускорить, применяя метод половинного деления, или бинарный поиск. Его идея заключается в следующем. Пусть фиксированный массив упорядочен по неубыванию (a_i ≤ a_{i + 1}). Случайно выбранный элемент am (обычно берут средний элемент) сравнивают с элементом поиска х. Если он меньше х, то искомый элемент может быть среди элементов a_{m + i}, …, а_n, т. е. в правой половине массива. Если он больше х — то среди элементов левой части массива. Если же он равен х, то поиск успешно заканчивается.

К стандартным задачам относятся задачи сортировки массива. Сортировка массива — это перерасположение элементов массива в заданном порядке. Основная цель сортировки — облегчить последующий поиск. Методы условно разделяют по главной идее алгоритма, а реализуются они целым семейством алгоритмов.

К простым методам сортировки относят:

• сортировку с помощью обмена (метод пузырька);
• сортировку с помощью прямого включения;
• сортировку с помощью выбора.

Сортировка с помощью обмена. При использовании этого метода сортировки соседние элементы массива сравниваются и при необходимости меняются местами до тех пор, пока массив не будет полностью упорядочен. Повторные проходы массива каждый раз сдвигают наименьший (наибольший) элемент оставшейся части массива к левому его концу. Метод широко известен под названием «пузырьковая сортировка», т. к. большие (меньшие) элементы массива, подобно пузырькам, «всплывают» на соответствующую позицию. Основной фрагмент программы содержит два вложенных цикла, причем внутренний цикл удобнее выбрать с убывающим шагом.

Алгоритм сортировки массива A(n) по возрастанию на псевдокоде:

Сортировка с помощью прямого включения (вставки). На каждом шаге этого метода массив разделен на две части: левую, уже отсортированную, и правую, еще не отсортированную. Первый элемент правой части вставляется в левую часть массива так, чтобы левая часть осталась отсортированной. В результате отсортированная часть увеличивается на один элемент, а неотсортированная — на один элемент уменьшается. Таким образом, на каждом шаге алгоритма сортировки вставками приходится выполнять две операции: поиск позиции для вставки элемента и собственно его вставку с последующим сдвигом на одну позицию вправо от элементов отсортированной части. Этот сдвиг «стирает» первый элемент неотсортированной части. Сначала отсортированным подмассивом считаем первый элемент, а остальная часть массива относится к неотсортированной части. Поскольку операции сравнения и перемещения чередуются друг с другом, этот способ сортировки часто называют просеиванием или погружением.

Сортировка с помощью прямого выбора. При сортировке этим методом сначала выбирается наименьший (наибольший) элемент массива и меняется местами с первым. Затем выбирается наименьший (наибольший) среди оставшихся (n – 1) элементов и меняется местами со вторым и т. д. до тех пор, пока не останется один наибольший (наименьший) элемент. Сортировка осуществляется с помощью двух вложенных циклов.

Приведенные алгоритмы сортировки не требуют дополнительной оперативной памяти. Время выполнения алгоритмов сортировки пропорционально количеству операций сравнения и перестановки элементов. Сортировка массива из $n$ элементов методом выбора главного элемента требует выполнения ${n^2}/{2}$ операций сравнения и n операций обмена элементами. Метод сортировки вставками требует ${n^2}/{4}$ операций сравнения и столько же операций обмена, а метод пузырьковой сортировки — ${n^2}/{2}$ операций сравнения и столько же операций обмена. Таким образом, из трех рассмотренных методов сортировки массива методы вставки и выбора приблизительно эквивалентны, а обменная сортировка — медленнее. Кроме того, что в методе вставки исходные элементы могут поступать последовательно, а в методе выбора они должны быть в наличии до начала сортировки.

Примеры решения задач

Пример 1. Одномерный массив, содержащий десять элементов, заполняется по следующему закону: A[1] = 1; A[2] = X; A[i] = 2 * X * A[i – 1] – A[i – 2], где i = 3, 4, …, 10. Каким будет значение A[5] при X = 1?

Решение. Представим значения первых пяти элементов массива А, полученные по заданному закону при Х = 1:

A[1] = 1; A[2] = Х = 1;

A[3] = 2 * Х * A[2] – A[1] = 2 * 1 * 1 – 1 = 1;

A[4] = 2 * Х * A[3] – A[2] = 2 * 1 * 1 – 1 = 1;

A[5] = 2 * Х * A[4] – A[3] = 2 * 1 * 1 – 1 = 1.

Таким образом, значение A[5] при Х = 1 будет равно 1.

Ответ: 1.

Пример 2. Задан двумерный массив А(n, n). Определить, что вычисляет приведенный фрагмент алгоритма:

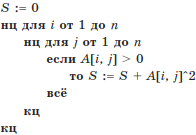
Решение. В данном алгоритме переменной S присваивается значение 0. Затем в структуре циклов по переменным i и j каждый из элементов массива А_ij сравнивается с нулем (А[i, j] > 0) и если элементы А_ij положительны, то квадраты А[i, j]^2 положительных элементов А_ij увеличивают значение суммы S (S := S + A[i, j]^2).

Ответ: фрагмент алгоритма вычисляет сумму квадратов положительных элементов массива.

Пример 3. Задан фрагмент алгоритма, использующий двумерный массив (таблицу) М(n, n), два одномерных массива A(n), B(n) и переменную X. Определить назначение массивов А и В и переменной.

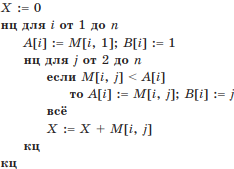
Решение. Представим фрагмент алгоритма словесно.

1. Переменной X присвоить значение 0.
2. Переменной i присвоить значение 1.
3. Если i ≤ n, то перейти к следующему пункту; в противном случае — конец фрагмента алгоритма.
4. Элементу одномерного массива А с индексом i присвоить значение элемента двумерного массива М, находящегося в i-й строке и первом столбце.
5. Элементу одномерного массива В с индексом i присвоить значение 1.
6. Переменной j присвоить значение 1.
7. Если j ≤ n, то перейти к следующему пункту; в противном случае — к п. 13.
8. Если М[i, j] < A[i], то перейти к следующему пункту; иначе — к п. 11.
9. Элементу A[i] присвоить значение элемента массива М, находящегося в i-й строке и j-м столбце.
10. Элементу В[i] присвоить значение переменной j.
11. Переменной Х присвоить значение суммы X + M[i, j].
12. Переменной j присвоить значение суммы j + 1 и вернуться к п. 7.
13. Переменной i присвоить значение суммы i + 1 и вернуться к п. 3.

Таким образом, анализ алгоритма показывает, что переменная X накапливала сумму всех элементов массива М; массив А — минимальные элементы соответствующих строк массива М; массив В — индексы (порядковые номера столбцов) минимальных элементов в соответствующих строках массива М.

Пример 4. Составить алгоритм определения наличия среди элементов главной диагонали заданной целочисленной матрицы A(n, m) хотя бы одного положительного нечетного элемента.

Решение. Для всех элементов А_ij главной диагонали выполняется условие i = j. Определение наличия нечетных элементов выполняется с помощью операции mod (остаток от целочисленного деления), при этом, если результат mod равен 1, — число нечетное.

Алгоритм:

Структурирование задачи при ее решении для использования вспомогательного
алгоритма. Вспомогательные алгоритмы: процедуры и функции

Разработка алгоритмов решения задач на компьютере требует определенных навыков. При построении алгоритма нужно стремиться к тому, чтобы запись алгоритма была понятной и наглядной. Кроме того, внося изменения в алгоритм, желательно не перестраивать его полностью. Эти требования можно удовлетворить, если придерживаться структурного подхода.

Самым важным преимуществом структурного подхода является возможность нисходящего программирования, благодаря которой можно двигаться от крупных задач к более мелким. Крупная задача будет разбиваться на менее крупные блоки, те в свою очередь — на меньшие блоки и т. д. Каждый блок алгоритма должен быть максимально самостоятельным и логически завершенным.

Разбиение на блоки должно определяться внутренней логикой задач. Процесс разбиения завершается, когда решение исходной задачи сводится к решению ряда простых задач, для которых легко построить алгоритм. На каждом шаге этого процесса происходит детализация, т. е. переход от общих задач к частным, которые в свою очередь детализируются в виде конкретных подзадач. Такой метод называется методом пошаговой детализации. Таким образом, при структурном подходе можно комбинировать не только базовые структуры (следование, ветвление, цикл), но и подключать алгоритмы, написанные ранее. Алгоритмы, которые целиком используются в составе других алгоритмов, называются вспомогательными, или подалгоритмами.

Если вспомогательный алгоритм в процессе работы программы выполняется многократно, отличаясь только параметрами, то обычно прибегают к оформлению вспомогательного алгоритма в виде подпрограммы — алгоритма-процедуры, или алгоритма-функции.

Подпрограмма — это именованный, логически законченный алгоритм, который оформляется специальным образом и может многократно использоваться при решении более общей задачи.

Описание подпрограмм можно сравнить с записываемой в математике формулой «в общем виде», в которую при расчетах подставляются конкретные значения. Далеко не каждую задачу можно свести к единственной формуле, но всегда можно записать алгоритм ее решения, а значит, подпрограмма — это инструкция по решению некоторой задачи. Как и формулу, подпрограмму можно использовать для обработки различных данных, передаваемых из главной программы или других подпрограмм.

В языках программирования подпрограмма является частью основной программы, ее описание располагается в описательной части программы. Структура подпрограммы такая же, как и основной программы; различие заключается лишь в оформлении заголовка подпрограммы. Заголовок подпрограммы состоит из служебного слова — идентификатора подпрограммы (имени подалгоритма) — и списка формальных параметров (список параметров не обязателен, допускаются подпрограммы без параметров). При вызове процедуры из текста программы вместо формальных параметров подставляются фактические параметры, при этом соблюдаются следующие правила:

• количество формальных и фактических параметров должно совпадать, причем соответствие между параметрами команды вызова и формальными параметрами процедуры устанавливается по порядку следования: первый фактический параметр соответствует первой переменной, записанной в заголовке подпрограммы, второй фактический параметр — второй переменной и т. д.;
• типы соответствующих параметров команды вызова и заголовка подпрограммы должны совпадать.

Команда вызова подпрограммы выполняется в три этапа:

1. вычисление фактических аргументов;
2. исполнение алгоритма подпрограммы;
3. присвоение полученных значений результатов алгоритма-подпрограммы соответствующим фактическим переменным.

Программа может содержать более одной подпрограммы; допускается использование вложенных подпрограмм, которые, в свою очередь, могут содержать свои вложенные подпрограммы.

Различают два вида подпрограмм — процедуры и функции. Имея один и тот же смысл и аналогичную структуру, процедуры и функции различаются назначением и способом их использования. Основное отличие функций от процедур заключается в том, что результатом выполнения функции является некоторое единственное значение. Функция — это алгоритмически вычисляемое выражение, которое присваивается идентификатору функции.

Подпрограммы бывают двух видов: стандартные и пользовательские. Стандартные, или встроенные, подпрограммы входят в состав языка программирования. Эти подпрограммы определенным образом организованы в специальные библиотеки. С помощью встроенных процедур и функций выполняются операции ввода/вывода, работа с файлами, обработка символьной информации, вычисление различных математических функций и т. п.

Подпрограммы, которые написаны пользователем, называются пользовательскими.

Технология программирования

Чтение короткой (30±50 строк) простой программы на алгоритмическом языке (языке программирования)

Запись алгоритма в словесной форме, в виде блок-схемы или на псевдокоде должна быть точна настолько, чтобы позволить исполнителю правильно выполнить алгоритм, при этом изображение команд произвольное. При решении любой задачи на компьютере предполагается, что некоторая информация подвергается обработке по предварительно составленной инструкции, называемой программой. Язык, на котором записывается алгоритм для исполнения компьютером, называется языком программирования. Языки программирования принадлежат к формальным языкам. При записи алгоритма на языке программирования все правила языка должны строго выполняться. Программа — это алгоритм, записанный на языке программирования.

Для записи программ используется конечный набор символов, составляющих алфавит языка программирования. В отличие от привычных алфавитов (например, русского) алфавит языка программирования включает в себя, кроме букв, цифры, знаки препинания, знаки арифметических действий и некоторые другие дополнительные символы. Программа записывается в виде последовательности символов из алфавита своего языка программирования. Естественно, что не любой текст, составленный из символов алфавита, будет правильной программой. Как и в естественных языках, правильность построения программы из символов алфавита можно проверить, используя синтаксис языка программирования.

Синтаксис языка программирования — это набор правил, которые определяют способы построения правильных программ из символов алфавита. Зная синтаксис языка, можно построить алгоритм, который определяет, является ли данный текст правильной программой или нет. Этот алгоритм позволяет компьютеру проверять синтаксическую правильность вводимых в него программ.

Должна быть определена и семантика языка программирования. Семантика языка программирования — это набор правил, по которым исполнитель выполняет программы на этом языке. Пользуясь семантикой языка, можно однозначно определить результат выполнения программы с заданными входными данными.

При чтении программы необходимо сначала определить, к какому виду она относится. Условно программы можно разделить на два вида: простая программа без использования подпрограмм (кроме стандартных процедур вводавывода) и программа, использующая подпрограммы (подалгоритмы). Такая программа может включать в свою структуру как стандартные подпрограммы, так и подпрограммы, написанные пользователем.

Для чтения простой программы необходимо выяснить:

• что является входными данными и как они вводятся в программу;
• какие действия последовательно выполняются с помощью каждого функционального узла программы (операторов), т. е. рассмотреть пошаговое выполнение операторов, при этом обратить внимание на роль вспомогательных переменных, массивов и т.д.;
• что является результаты работы программы;
• каковы ограничения по работе алгоритма.

При чтении программы, использующей подпрограммы, необходимо сначала проанализировать, что и как выполняют подпрограммы, каковы их входные и выходные параметры. Затем в основной программе вызовы каждой из подпрограмм рассматривать уже как результат работы соответствующего подалгоритма.

Существенно облегчает чтение программ наличие комментариев — поясняющего текста. Комментарии можно добавлять в любое место программы. Наличие комментариев — обязательное условие хорошо и грамотно написанной программы.

Примеры чтения программ на языках Pascal, QBASIC

Примечание. В приведенных примерах программа приводится для двух языков программирования. В зависимости от того, какой язык программирования изучается, и следует рассматривать ее вариант записи и соответствующие пояснения.

Пример 1. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем тексты программы:

1. формируется тело программы и описываются переменные;
2. вводятся натуральные числа М и N, причем проверяется условие корректности ввода: числа должны быть положительные. Если введенные значения не удовлетворяют условию, то ввод повторяют, пока условие не будет выполнено;
3. выбирается наименьшее значение из М и N, результат записывается в K;
4. NOD присваивается значение 1;
5. в цикле от двух до K генерируется число I;
6. тело цикла — в условном операторе проверяется, является ли значение переменной I одновременно делителем М и N. Если условие выполняется, то текущее значение I сохраняется в переменной NOD; если условие не выполняется, NOD не изменит своего значения;
7. после перебора всех значений I в NOD или запишется наибольший делитель двух чисел М и N, или останется значение 1;
8. последний оператор программы служит для вывода результата работы программы — значения переменной NOD.

Переменные, используемые в программе:

N, М — исследуемые числа;

I — переменная цикла;

NOD — наибольший общий делитель;

К — наименьшее из М и N.

Ответ: данная программа позволяет определить для двух чисел М и N их наибольший общий делитель NOD.

Примечание. Эту же задачу можно решить, используя алгоритм Евклида.

Пример 2. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем тексты программы:

1. формируется тело программы, описываются переменные и одномерный массив MAS целого типа (для Pascal целый массив длиной 100);
2. вводится фактическая длина массива N с проверкой на положительное значение N;
3. вводится значение первого элемента массива MAS;
4. устанавливается начальное значение МАХ по первому элементу массива;
5. переменной К присваивается значение 1;
6. последовательно, в цикле, просматриваются вводимые элементы массива, и если очередной элемент MAS(I) больше или равен МАХ, то переписывается значение MAS(I) в МАХ и в переменной К запоминается I;
7. выводятся результаты: МАХ — значение максимального элемента массива и К — номер максимального элемента в исходном массиве (если таких элементов несколько, выведется номер самого правого максимума).

Переменные, используемые в программе:

MAS — массив чисел;

N — размер массива;

I — переменная цикла;

МАХ — значение наибольшего элемента;

К — номер наибольшего элемента.

Ответ: программа написана для поиска значения максимального элемента массива и его номера (если таких элементов несколько, то будет найден номер самого правого максимума).

Пример 3. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем тексты программы:

1. формируется тело программы и описываются переменные;
2. вводится строка символов S;
3. определяется длина строки, значение которой заносится в переменную L;
4. в цикле осуществляется замена ‘!’ на ‘.’ в исходной строке;
5. выводится преобразованная строка.

Переменные, используемые в программе:

I — переменная цикла;

L — длина строки;

S — строка текста.

В программе на языке Pascal используется встроенная функция языка:

Length(STR) — она определяет фактическую длину строки STR (длина строки не более 256 символов).

В программе на языке QBASIC используются встроенные функции:

Len(X) — определяет фактическую длину строки X (длина строки не более 256 символов);

M1D$(X$, N, M) — выделяет M символов, начиная с N-го символа в символьном выражении X$ (M можно опустить).

Ответ: данная программа позволяет заменить во введенной строке символов все восклицательные знаки на точки.

Пример 4. Дана программа на двух языках программирования. Определить, какую задачу она решает.

Решение. Проанализируем текст программы на языке Pascal:

1. формируется тело программы и описываются переменные;
2. вводится строка STR и дублируется во вспомогательной переменной S1;
3. определяется местоположение первой точки в тексте; если точка есть, то из S1 вырезается текст до нее;
4. ищется вторая точка; если она есть, то из S1 вырезается текст после нее;
5. в зависимости от присутствия точек результат выводится на экран.

Используемые переменные:

I — номер позиции, которая соответствует точке;

STR — строка текста;

S1 — вспомогательная переменная.

В данной программе используются встроенные функции языка Pascal:

Pos(S1, S2) — поиск подстроки S1 в строке S2 ;

Delete(S, N, M) — удаление из строки S M символов, начиная с позиции N;

Copy(S, N, M) — выделение подстроки из M символов, которые располагаются в строке S начиная с позиции N.

Проанализируем текст программы на языке QBASIC:

1. формируется тело программы, и описываются переменные;
2. вводится строка символов S;
3. определяется местоположение первой точки в тексте — М1;
4. ищется вторая точка в строке (поиск начинается с символа М1 + 1); если в строке есть две точки, то на экран выводится текст, находящийся между двумя точками, если нет — сообщение «В тексте нет двух точек».

Используемые переменные:

S — строка текста;

Ml, M2 — номера позиций двух точек; если точек нет, то значения Ml и М2 равны нулю.

В данной программе используются встроенные функции языка:

INSTR(N, X$, Y$) — поиск подстроки Y в строке X, начиная с N-го символа (N можно опустить);

MID$(X$, N, M) — выделение M символов, начиная с N-го символа в символьном выражении X$ (M можно опустить).

Ответ: данная программа из заданной строки символов выделяет подстроку между первой и второй точкой.

Пример 5. Проанализировать тексты программы.

Решение.

1. Формируется тело программы и описываются переменные и двумерный массив MАS;
2. вводится фактический размер массива MAS и значения его элементов;
3. просматриваются строки массива справа налево, находиться минимальный элемент в строке и запоминаются значения индексов (номер столбца) этого элемента;
4. для каждой строки выводится значение и местоположение самого правого минимального элемента.

Используемые переменные:

MAS — двумерный массив;

N, M — количество строк и столбцов массива;

I, J — переменные цикла;

JM — столбец минимального элемента для данной строки;

MIN — текущий минимум.

Ответ: программа решает задачу поиска в каждой строке двумерной матрицы минимального элемента и его координат. Если таких элементов в строке несколько, то выводится значение и координаты самого правого элемента.

Поиск и исправление ошибок в небольшом фрагменте программы (10±20 строк)

Существует три аспекта проверки программы:

1. на правильность;
2. на эффективность реализации;
3. на вычислительную сложность.

Эти проверки, вместе взятые, направлены на получение экспериментального ответа на вопросы: работает ли алгоритм и насколько хорошо он работает? Предполагается, что проверка правильности удостоверяет, что программа делает в точности то, для чего она была предназначена. Проверка эффективности реализации направлена на поиск способов «заставить» правильную программу работать быстрее или расходовать меньше памяти. Чтобы улучшить программу, пересматриваются результаты этапа реализации в процессе построения алгоритма.

Проверка вычислительной сложности сводится к экспериментальному анализу сложности алгоритма или к экспериментальному сравнению двух или более алгоритмов, решающих одну и ту же задачу.

Наличие ошибок в только что разработанной программе — вполне нормальное, закономерное явление. Составить реальную (достаточно сложную) программу без ошибок практически невозможно. Нельзя делать вывод, что программа правильна, лишь на том основании, что она считает и выдает результаты.

Текст программы можно проконтролировать за столом с помощью просмотра, проверки и прокрутки.

Просмотр. Текст программы просматривается на предмет обнаружения явных ошибок и расхождений с алгоритмом. Нужно просмотреть организацию всех циклов, чтобы убедиться в правильности операторов, задающих кратности циклов. Полезно просмотреть еще раз условия в условных операторах, аргументы в обращениях к подпрограммам и т. п.

Проверка. При проверке программы программист по тексту программы мысленно старается восстановить тот вычислительный процесс, который определяет программа, после чего сверяет его с требуемым алгоритмом.

Прокрутка. Основой прокрутки является имитация программистом за столом выполнения программы на машине. Для выполнения прокрутки приходится задаваться какими-то исходными данными и производить над ними необходимые вычисления.

Прокрутка — трудоемкий процесс, поэтому ее следует применять только для контроля логически сложных участков программы.

После просмотра программы вручную ее необходимо отладить и протестировать на компьютере.

Отладка — это процесс поиска и устранения ошибок в программе, производимый по результатам ее прогона на компьютере.

Тестирование — это испытание, проверка правильности работы программы в целом или ее составных частей.

Отладка и тестирование — два разных этапа:

• при отладке происходит локализация и устранение синтаксических ошибок и явных ошибок кодирования;
• в процессе тестирования проверяется работоспособность программы, не содержащей явных ошибок. Тестирование устанавливает факт наличия ошибок, а отладка выясняет их причину.

Как бы тщательно ни была отлажена программа, решающим этапом, устанавливающим ее пригодность для работы, является контроль программы по результатам ее выполнения на системе тестов. Программу условно можно считать правильной, если ее запуск для выбранной системы тестовых исходных данных во всех случаях дает правильные результаты.

Тестовые данные должны обеспечить проверку всех возможных условий возникновения ошибок. Процесс тестирования можно разделить на три этапа:

1. Проверка в нормальных условиях. Предполагает тестирование на основе данных, которые характерны для реальных условий функционирования программы.
2. Проверка в экстремальных условиях. Тестовые данные включают граничные значения области изменения входных переменных, которые должны восприниматься программой как правильные данные. Типичными примерами таких значений являются очень маленькие или очень большие числа и отсутствие данных. Еще один тип экстремальных условий — граничные объемы данных. Например, когда массивы состоят из слишком малого или слишком большого количества элементов.
3. Проверка в исключительных ситуациях. Проводится с использованием данных, значения которых лежат за пределами допустимой области изменений.

Ошибки могут быть допущены на всех этапах решения задачи. Разновидности характерных ошибок:

• Неправильная постановка задачи — верное решение неверно сформулированной задачи.
• Неверный алгоритм — выбор алгоритма, приводящего к неточному, неэффективному решению задачи.
• Ошибки анализа — неполный учет ситуаций, которые могут возникнуть; логические ошибки.
• Семантические ошибки — неправильный порядок выполнения операций.
• Синтаксические ошибки — нарушение правил, определяемых языком программирования.
• Ошибки при выполнении операций — слишком большое число (переполнение), деление на нуль, извлечение квадратного корня из отрицательного числа и т. п.
• Ошибки в данных — неправильное определение возможного диапазона изменения данных.
• Опечатки — перепутаны близкие по написанию символы, например цифра 1 и буква I.
• Ошибки ввода/вывода — неверное считывание входных данных, неверное задание форматов, отсутствие некоторых данных.

В качестве примера рассмотрим программу, в которой вычисляется значение функции по приведенным формулам в зависимости от значения параметра K, который является номером режима.

$y(x)={table√{a_1x^2+b_1x+c_1}, text»если» K=1; √{a_2x^2+c_2}, text»если» K=2; √{b_3x+c_3}, text»если» K=3;$

Программа имеет вид

Ошибки, допущенные при написании программы:

1. Пропущен ввод исходных данных А1, B1, C1, A2, C2, B3, C3; пропущено описание переменной Y (для языка Pascal).
2. В приведенной программе не предусмотрена обработка ситуации, когда под корнем получается отрицательное значение. Необходимо использовать условный оператор для определения положительности подкоренного выражения.
3. Отсутствует анализ ситуации, когда вместо цифр 1, 2, 3 для переменной К считана другая цифра. В этом случае, можно выдавать, например, сообщение: «Номер режима неверен». Для выдачи такого сообщения в программе в саsе-операторе после строки с меткой 3 нужно добавить строку вида else <Печать сообщения> (вариант 1). Можно также организовать ввод параметра K с проверкой введенного значения, и при ошибочном вводе требовать повторения ввода значения для переменной K (вариант 2).

Пример откорректированной программы (вариант 1).

Пример откорректированной программы (вариант 2).

Создание собственной программы (30±50 строк) для решения простых задач

Процесс создания компьютерной модели можно представить как путь от постановки задачи до реализации модели на компьютере. При разработке компьютерной модели очень важен выбор программного обеспечения (ПО), с помощью которого будет реализована модель. Возможны два основных варианта выбора — это, во-первых, прикладное ПО и, во-вторых, среда программирования. Если в качестве ПО была выбрана среда программирования, то построение компьютерной модели завершается созданием программы.

При написании программы прежде всего следует четко уяснить задачу, которую должна решать программа. Затем предварительно разработанный алгоритм решения задачи записывается в виде упорядоченной последовательности команд (инструкций), т. е. составляется программа, ориентированная на определенную среду программирования.

При написании программы обязательно следует проверять, насколько она соответствует намеченной цели, т. е. делает ли программа для всех наборов данных то, что от нее требуется, не выполняет ли она каких-либо лишних действий. Основное внимание следует сосредоточить на предотвращении логических ошибок. Для этого рекомендуется перед написанием программы построить блок-схему алгоритма решения или словесный алгоритм, что позволит абстрагироваться от конкретного языка программирования и сосредоточиться на анализе алгоритма.

Примеры разработки программ

Пример 1. Составить словесный алгоритм, разработать блок-схему и написать программу проверки принадлежности введенного числа данной арифметической прогрессии. Прогрессия задается двумя последовательными членами.

Решение. Словесный алгоритм.

Начало алгоритма

1. Ввести два последовательных члена арифметической прогрессии: A1, A2.
2. Ввести произвольное целое число C.
3. Найти разность (D) арифметической прогрессии.
4. Найти разность между введенным числом C и членом арифметической прогрессии, например A1.
5. Найти остаток от деления нацело найденной разности на D.
6. Если остаток от деления равен 0, то это значит, что число C принадлежит рассматриваемой арифметической прогрессии»; иначе получаем, что число C не принадлежит рассматриваемой арифметической прогрессии.

Конец алгоритма.

Блок-схема алгоритма:

Программа:

Примечание. Mod — операция, результатом которой является остаток от целочисленного деления.

Пример 2. Составить словесный алгоритм, алгоритм в виде блок-схемы и написать программу поиска в строковом массиве, содержащем фамилии 10 учеников, заданной фамилии, обеспечить запоминание ее порядкового номера (массив фамилий может быть неупорядочен).

Решение.

Словесный алгоритм

Начало алгоритма

1. Ввести все десять фамилий (строковый массив из 10 элементов).
2. Ввести фамилию, которую нужно найти.
3. Сравнивать ее с очередным элементом строкового массива, пока не будет найдена такая же фамилия или пока не закончится список (массив).
4. Если фамилия найдена, вывести ее номер в списке (массиве), если нет — сообщить о том, что фамилия не найдена.

Конец алгоритма.

Блок-схема алгоритма

Программа:

Общее понятия алгоритма. Основные свойства алгоритма
ПОНЯТИЕ АЛГОРИТМА. СВОЙСТВА АЛГОРИТМА. ВИДЫ АЛГОРИТМОВ. 
СПОСОБЫ ОПИСАНИЯ АЛГОРИТМОВ
Алгоритмом называется точное и понятное предписаниe исполнителю совершить 
последовательность действий, направленных на решение поставленной задачи. Слово 
«алгоритм» происходит от имени математика Аль Хорезми, который сформулировал 
правила выполнения арифметических действий. Первоначально под алгоритмом понимали 
только правила выполнения четырех арифметических действий над числами. В дальнейшем
это понятие стали использовать вообще для обозначения последовательности действий, 
приводящих к решению любой поставленной задачи. Говоря об алгоритме вычислительного
процесса, необходимо понимать, что объектами, к которым применялся алгоритм, 
являются данные. Алгоритм решения вычислительной задачи представляет собой 
совокупность правил преобразования исходных данных в результатные.
Основными свойствами алгоритма являются:
1. детерминированность (определенность). Предполагает получение однозначного 
результата вычислительного процecca при заданных исходных данных. Благодаря 
этому свойству процесс выполнения алгоритма носит механический характер;
2. результативность. Указывает на наличие таких исходных данных, для которых 
реализуемый по заданному алгоритму вычислительный процесс должен через 
конечное число шагов остановиться и выдать искомый результат;
3. массовость. Это свойство предполагает, что алгоритм должен быть пригоден для 
решения всех задач данного типа;
4. дискретность. Означает расчлененность определяемого алгоритмом вычислительного
процесса на отдельные этапы, возможность выполнения которых исполнителем 
(компьютером) не вызывает сомнений.
Алгоритм должен быть формализован по некоторым правилам посредством конкретных 
изобразительных средств. К ним относятся следующие способы записи алгоритмов: 
словесный, формульно­словесный, графический, язык операторных схем, алгоритмический 
язык.
Наибольшее распространение благодаря своей наглядности получил графический (блок­
схемный) способ записи алгоритмов. Блок­схемой называется графическое изображение логической структуры алгоритма, в 
котором каждый этап процесса обработки информации представляется в виде 
геометрических символов (блоков), имеющих определенную конфигурацию в зависимости 
от характера выполняемых операций. Перечень символов, их наименование, отображаемые 
ими функции, форма и размеры определяются ГОСТами.
При всем многообразии алгоритмов решения задач в них можно выделить три основных 
вида вычислительных процессов:
 линейный;
 ветвящийся;
 циклический.
Линейным называется такой вычислительный процесс, при котором все этапы решения 
задачи выполняются в естественном порядке следования записи этих этапов.
Ветвящимся называется такой вычислительный процесс, в котором выбор направления 
обработки информации зависит от исходных или промежуточных данных (от результатов 
проверки выполнения какого­либо логического условия).
Циклом называется многократно повторяемый участок вычислений. Вычислительный 
процесс, содержащий один или несколько циклов, называется циклическим. По 
количеству выполнения циклы делятся на циклы с определенным (заранее заданным) 
числом повторений и циклы с неопределенным числом повторений. Количество повторений
последних зависит от соблюдения некоторого условия, задающего необходимость 
выполнения цикла. При этом условие может проверяться в начале цикла — тогда речь идет
о цикле с предусловием, или в конце — тогда это цикл с постусловием.
АЛГОРИТМ – система правил, сформулированная на понятном исполнителю языке, 
которая определяет процесс перехода от допустимых исходных данных к некоторому 
результату и обладает свойствами массовости, конечности, определенности, 
детерминированности.
Слово «алгоритм» происходит от имени великого среднеазиатского ученого 8–9 вв. Аль­
Хорезми (Хорезм – историческая область на территории современного Узбекистана). Из 
математических работ Аль­Хорезми до нас дошли только две – алгебраическая (от названия этой книги родилось слово алгебра) и арифметическая. Вторая книга долгое 
время считалась потерянной, но в 1857 в библиотеке Кембриджского университета был 
найден ее перевод на латинский язык. В ней описаны четыре правила арифметических 
действий, практически те же, что используются и сейчас. Первые строки этой книги были 
переведены так: «Сказал Алгоритми. Воздадим должную хвалу Богу, нашему вождю и 
защитнику». Так имя Аль­Хорезми перешло в Алгоритми, откуда и появилось слово 
алгоритм. Термин алгоритм употреблялся для обозначения четырех арифметических 
операций, именно в таком значении он и вошел в некоторые европейские языки. Например, 
в авторитетном словаре английского языка Webster’sNew World Dictionary, изданном в 
1957, слово алгоритм снабжено пометкой «устаревшее» и объясняется как выполнение 
арифметических действий с помощью арабских цифр.
Слово «алгоритм» вновь стало употребительным с появлением электронных 
вычислительных машин для обозначения совокупности действий, составляющих некоторый
процесс. Здесь подразумевается не только процесс решения некоторой математической 
задачи, но и кулинарный рецепт и инструкция по использованию стиральной машины, и 
многие другие последовательные правила, не имеющие отношения к математике, – все эти 
правила являются алгоритмами. Слово «алгоритм» в наши дни известно каждому, оно 
настолько уверенно шагнуло в разговорную речь, что сейчас нередко на страницах газет, в 
выступлениях политиков встречаются выражения «алгоритм поведения», «алгоритм 
успеха» и т.д.
Проблема определения понятия «алгоритм». На протяжении многих веков понятие 
алгоритма связывалось с числами и относительно простыми действиями над ними, да и 
сама математика была, по большей части, наукой о вычислениях, наукой прикладной. Чаще
всего алгоритмы представлялись в виде математических формул. Порядок элементарных 
шагов алгоритма задавался расстановкой скобок, а сами шаги заключались в выполнении 
арифметических операций и операций отношения (проверки равенства, неравенства и т.д.). 
Часто вычисления были громоздкими, а вычисления вручную – трудоемкими, но суть 
самого вычислительного процесса оставалась очевидной. У математиков не возникала 
потребность в осознании и строгом определении понятия алгоритма, в его обобщении. Но с
развитием математики появлялись новые объекты, которыми приходилось оперировать: 
векторы, графы, матрицы, множества и др. Как определить для них однозначность или как 
установить конечность алгоритма, какие шаги считать элементарными? В 1920­х задача 
точного определения понятия алгоритма стала одной из центральных проблем математики.
В то время существовало две точки зрения на математические проблемы:
Все проблемы алгоритмически разрешимы, но для некоторых алгоритм еще не найден, 
поскольку еще не развиты соответствующие разделы математики. Есть проблемы, для которых алгоритм вообще не может существовать.
Идея о существовании алгоритмически неразрешимых проблем оказалась верной, но для 
того, чтобы ее обосновать, необходимо было дать точное определение алгоритма. Попытки 
выработать такое определение привели к возникновению теории алгоритмов, в которую 
вошли труды многих известных математиков – К.Гедель, К.Черч, С.Клини, А.Тьюринг, 
Э.Пост, А.Марков, А.Колмогоров и многие другие.
Точное определение понятия алгоритма дало возможность доказать алгоритмическую 
неразрешимость многих математических проблем.
Появление первых проектов вычислительных машин стимулировало исследование 
возможностей практического применения алгоритмов, использование которых, ввиду их 
трудоемкости, было ранее недоступно. Дальнейший процесс развития вычислительной 
техники определил развитие теоретических и прикладных аспектов изучения алгоритмов.
Понятие «алгоритма». В повседневной жизни каждый человек сталкивается с 
необходимостью решения задач самой разной сложности. Некоторые из них трудны и 
требуют длительных размышлений для поиска решений (а иногда его так и не удается 
найти), другие же, напротив, столь просты и привычны, что решаются автоматически. При 
этом выполнение даже самой простой задачи осуществляется в несколько 
последовательных этапов (шагов). В виде последовательности шагов можно описать 
процесс решения многих задач, известных из школьного курса математики: приведение 
дробей к общему знаменателю, решение системы линейных уравнений путем 
последовательного исключения неизвестных, построение треугольника по трем сторонам с 
помощью циркуля и линейки и т.д. Такая последовательность шагов в решении задачи 
называется алгоритмом. Каждое отдельное действие – это шаг алгоритма. 
Последовательность шагов алгоритма строго фиксирована, т.е. шаги должны быть 
упорядоченными. Правда, существуют параллельные алгоритмы, для которых это 
требование не соблюдается.
Понятие алгоритма близко к другим понятиям, таким, как метод (метод Гаусса решения 
систем линейных уравнений), способ (способ построения треугольника по трем сторонам с 
помощью циркуля и линейки). Можно сформулировать основные особенности именно 
алгоритмов.
Наличие исходных данных и некоторого результата. Алгоритм – это точно 
определенная инструкция, последовательно применяя которую к исходным данным, можно
получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных 
чисел делимое может быть любым, а делитель не может быть равен нулю.
Массовость, т.е. возможность применять многократно один и тот же алгоритм. Алгоритм 
служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. 
Так алгоритм сложения применим к любой паре натуральных чисел.
Детерминированность. При применении алгоритма к одним и тем же исходным данным 
должен получаться всегда один и тот же результат, поэтому, например, процесс 
преобразования информации, в котором участвует бросание монеты, не является 
детерминированным и не может быть назван алгоритмом.
Результативность. Выполнение алгоритма должно обязательно приводить к его 
завершению. В то же время можно привести примеры формально бесконечных алгоритмов, 
широко применяемых на практике. Например, алгоритм работы системы сбора 
метеорологических данных состоит в непрерывном повторении последовательности 
действий («измерить температуру воздуха», «определить атмосферное давление»), 
выполняемых с определенной частотой (через минуту, час) во все время существования 
данной системы.
Определенность. На каждом шаге алгоритма у исполнителя должно быть достаточно 
информации, чтобы его выполнить. Кроме того, исполнителю нужно четко знать, каким 
образом он выполняется. Шаги инструкции должны быть достаточно простыми, 
элементарными, а исполнитель должен однозначно понимать смысл каждого шага 
последовательности действий, составляющих алгоритм (при вычислении площади 
прямоугольника любому исполнителю нужно уметь умножать и трактовать знак «x» именно
как умножение). Поэтому вопрос о выборе формы представления алгоритма очень важен. 
Фактически речь идет о том, на каком языке записан алгоритм.
Формы представления алгоритмов. Для записи алгоритмов необходим некоторый язык, 
при этом очень важно, какой именно язык выбран. Записывать алгоритмы на русском языке
(или любом другом естественном языке) громоздко и неудобно.
Например, описание алгоритма Евклида нахождения НОД (наибольшего общего делителя) 
двух целых положительных чисел может быть представлено в виде трех шагов. Шаг 1: 
Разделить m на n. Пусть p – остаток от деления.
Шаг 2: Если p равно нулю, то n и есть исходный НОД.
Шаг 3: Если p не равно нулю, то сделаем m равным n, а n равным p. Вернуться к шагу 1. Приведенная здесь запись алгоритма нахождения НОД очень упрощенная. Запись, данная 
Евклидом, представляет собой страницу текста, причем последовательность действий 
существенно сложней.
Одним из распространенных способов записи алгоритмов является запись на языке блок­
схем. Запись представляет собой набор элементов (блоков), соединенных стрелками. 
Каждый элемент – это «шаг» алгоритма. Элементы блок­схемы делятся на два вида. 
Элементы, содержащие инструкцию выполнения какого­либо действия, обозначают 
прямоугольниками, а элементы, содержащие проверку условия – ромбами. Из 
прямоугольников всегда выходит только одна стрелка (входить может несколько), а из 
ромбов – две (одна из них помечается словом «да», другая – словом «нет», они 
показывают, соответственно, выполнено или нет проверяемое условие).
На рисунке представлена блок­схема алгоритма нахождения НОД:
Построение блок­схем из элементов всего лишь нескольких типов дает возможность 
преобразовать их в компьютерные программы и позволяет формализовать этот процесс.
Формализация понятия алгоритмов. Теория алгоритмов. Приведенное определение 
алгоритма нельзя считать представленным в привычном математическом смысле. 
Математические определения фигур, чисел, уравнений, неравенств и многих других 
объектов очень четки. Каждый математически определенный объект можно сравнить с 
другим объектом, соответствующим тому же определению. Например, прямоугольник 
можно сравнить с другим прямоугольником по площади или по длине периметра. 
Возможность сравнения математически определенных объектов – важный момент 
математического изучения этих объектов. Данное определение алгоритма не позволяет сравнивать какие­либо две таким образом определенные инструкции. Можно, например, 
сравнить два алгоритма решения системы уравнений и выбрать более подходящий в данном
случае, но невозможно сравнить алгоритм перехода через улицу с алгоритмом извлечения 
квадратного корня. С этой целью нужно формализовать понятие алгоритма, т.е. отвлечься 
от существа решаемой данным алгоритмом задачи, и выделить свойства различных 
алгоритмов, привлекая к рассмотрению только его форму записи. Задача нахождения 
единообразной формы записи алгоритмов, решающих различные задачи, является одной из 
основных задач теории алгоритмов. В теории алгоритмов предполагается, что каждый шаг 
алгоритма таков, что его может выполнить достаточно простое устройство (машина), 
Желательно, чтобы это устройство было универсальным, т.е. чтобы на нем можно было 
выполнять любой алгоритм. Механизм работы машины должен быть максимально простым 
по логической структуре, но настолько точным, чтобы эта структура могла служить 
предметом математического исследования. Впервые это было сделано американским 
математиком Эмилем Постом в 1936 (машина Поста) еще до создания современных 
вычислительных машин и (практически одновременно) английским математиком Аланом 
Тьюрингом (машина Тьюринга).
История конечных автоматов: машина Поста и машина Тьюринга. Машина Поста – 
абстрактная вычислительная машина, предложенная Постом (Emil L.Post), которая 
отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были 
созданы для уточнения понятия «алгоритм».
В 1935 американский математик Пост опубликовал в «Журнале символической логики» 
статью Финитные комбинаторные процессы, формулировка 1. В этой статье и 
появившейся одновременно в Трудах Лондонского математического общества статье 
английского математика Тьюринга О вычислимых числах с приложением к проблеме 
решения были даны первые уточнения понятия «алгоритм». Важность идей Поста состоит 
в том, что был предложен простейший способ преобразования информации, именно он 
построил алгоритмическую систему (алгоритмическая система Поста). Пост доказал, что 
его система обладает алгоритмической полнотой. В 1967 профессор В.Успенский 
пересказал эти статьи с новых позиций. Он ввел термин «машина Поста». Машина Поста – 
абстрактная машина, которая работает по алгоритмам, разработанным человеком, она 
решает следующую проблему: если для решения задачи можно построить машину Поста, то
она алгоритмически разрешима. В 1970 машина Поста была разработана в металле в 
Симферопольском университете. Машина Тьюринга была построена в металле в 1973 в 
Малой Крымской Академии Наук.
Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на 
одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V». У машины есть головка, которая может перемещаться вдоль ленты на одну клетку 
вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, 
стирать метку, если она была, либо проверять наличие в клетке метки. Информация о 
заполненных метками клетках ленты характеризует состояние ленты, которое может 
меняться в процессе работы машины. В каждый момент времени головка находится над 
одной из клеток ленты и, как говорят, обозревает ее. Информация о местоположения 
головки вместе с состоянием ленты характеризует состояние машины Поста. Работа 
машины Поста заключается в том, что головка передвигается вдоль ленты (на одну клетку 
за один шаг) влево или вправо, наносит или стирает метки, а также распознает, есть ли 
метка в клетке в соответствии с заданной программой, состоящей из отдельных команд.
Машина Тьюринга состоит из счетной ленты (разделенной на ячейки и ограниченной слева, 
но не справа), читающей и пишущей головки, лентопротяжного механизма и операционного
исполнительного устройства, которое может находиться в одном из дискретных 
состояний q0, q1, …, qs , принадлежащих некоторой конечной совокупности (алфавиту 
внутренних состояний), при этом q0 называется начальным состоянием. Читающая и 
пишущая головка может читать буквы рабочего алфавита A = {a0, a1, …, at}, стирать их и 
печатать. Каждая ячейка ленты в каждый момент времени занята буквой из множества А. 
Чаще всего встречается буква а0 – «пробел». Головка находится в каждый момент времени
над некоторой ячейкой ленты – текущей рабочей ячейкой. Лентопротяжный механизм 
может перемещать ленту так, что головка оказывается над соседней ячейкой ленты, при 
этом возможна ситуация выхода за левый край ленты, которая является аварийной 
(недопустимой), или машинного останова, когда машина выполняет предписание об 
остановке.
Современный взгляд на алгоритмизацию. Теория алгоритмов строит и изучает 
конкретные модели алгоритмов. С развитием вычислительной техники и теории 
программирования возрастает необходимость построения новых экономичных алгоритмов,
изменяются способы их построения, способы записи алгоритмов на языке, понятном 
исполнителю. Особый тип исполнителя алгоритмов – компьютер, поэтому необходимо 
создавать специальные средства, позволяющие, с одной стороны, разработчику в удобном 
виде записывать алгоритмы, а с другой – дающие компьютеру возможность понимать 
написанное. Такими средствами являются языки программирования или алгоритмические 
языки.
Анна Чугайнова
ЛИТЕРАТУРА Тьюринг А. Может ли машина мыслить? М., Мир, 1960 
Успенский В. Машина Поста. Наука, 1988 
Кормен Т., Лейзерсон, Ривес Р. Алгоритмы. Построение и анализ. М., МЦНМО, 1999
ВЫЧИСЛИМОСТЬ. ВВЕДЕНИЕ В ТЕОРИЮ АЛГОРИТМОВ
©  2000 г. Е. П. Емельченков,  В. Е. Емельченков 
Рассматриваются основные понятия теории алгоритмов. Исследуется 
неразрешимость многих проблем важных для теоретического программирования. 
Понятие алгоритма является не только центральным понятием теории 
алгоритмов, не только одним из главных понятий математики вообще, но одним 
из главных понятий современной науки. Более того, сегодня, с наступлением эры 
информатики, алгоритмы становятся одним из важнейших факторов 
цивилизации.
Успенский В.А., Семенов А.Л. [1, c. 10]
Введение
Точное понятие «алгоритм» было выработано лишь в тридцатых годах XX века. До этого 
математики довольствовались интуитивным понятием алгоритма. Это объясняется тем, 
что до середины XIX века математика имела дело в основном с числами и вычислениями. 
Понятие алгоритма отождествлялось с понятием метода вычислений. Все многообразие 
вычислений комбинировалось из четко определенных операций арифметики, 
тригонометрии и анализа. Поэтому понятие метода вычисления считалось интуитивно 
ясным и не нуждалось в специальных исследованиях.
Новые более жесткие требования к строгости стимулировались в основном математикой 
нечисловых объектов во второй половине XIX века. Одним из решающих обстоятельств, 
приведших к пересмотру оснований математики, явилось создание Кантором теории 
множеств.
Опыт парадоксов теории множеств научил математику крайне осторожно обращаться с 
бесконечностью и даже о бесконечности рассуждать с помощью финитных методов. 
Существо финитного подхода заключается в том, что он допускает только конечные 
комплексы действий над конечным числом объектов. Выяснение того, какие объекты и действия над ними следует считать точно определенными, какими свойствами и 
возможностями обладают комбинации элементарных действий, что можно и чего нельзя 
сделать с их помощью ­ все это стало предметом теории алгоритмов. Главным 
внутриматематическим приложением теории алгоритмов явились доказательства 
невозможности алгоритмического решения некоторых математических проблем. Такие 
доказательства неосуществимы без точного понятия алгоритма (для доказательства 
несуществования алгоритма решения того или иного класса задач, надо точно знать 
несуществование чего требуется доказать).
1. Интуитивное понятие алгоритма
Человек ежедневно встречается с множеством задач, возникающих в различных областях 
деятельности общества, например:
а) подготовиться к уроку по математике;
б) приготовить раствор для проявления фотопленки;
в) избавиться от лишнего веса.
Для решения задач надо знать, что дано, и что следует получить. Другими 
словами, задача представляет собой совокупность двух объектов: исходных данных и 
искомых результатов. Чтобы получить результаты, необходимо знать метод решения 
задачи, то есть располагать предписанием (инструкцией, правилом), в котором указано, 
какие действия и в каком порядке следует выполнить, чтобы решить задачу (получить 
искомые результаты). Предписание, определяющее порядок выполнения действий над 
данными с целью получения искомых результатов, называется алгоритмом.
Алгоритм ­ это точная конечная система правил, определяющая содержание и порядок 
действий исполнителя над некоторыми объектами (исходными и промежуточными 
данными) для получения (после конечного числа шагов) искомого результата.
Следует иметь в виду, что это ­ не определение в математическом смысле слова, но 
довольно подробное описание понятия алгоритма, раскрывающее его сущность. Описание 
может быть другим. Так, в школьном учебнике по информатике [l] понятие алгоритма 
дается в следующей форме: «Под алгоритмом понимают понятное и точное предписание 
исполнителю совершить последовательность действий, направленных на решение 
поставленной задачи».
Понятие алгоритма является одним из основных понятий современной математики и 
является объектом исследования специального раздела математики ­ теории алгоритмов. Еще на самых ранних ступенях развития математики в ней стали возникать различные 
вычислительные процессы чисто механического характера. С их помощью искомые 
величины ряда задач вычислялись последовательно из исходных величин по определенным 
правилам. К числу таких правил относились и правила выполнения арифметических 
операций над числами.
Столетия эти правила были очень сложны и не удивительно поэтому, что производить 
вычисления с большими числами могли только люди с высшим образованием. Так, чтобы 
научиться арифметическому делению в средние века требовалось закончить университет. 
Да еще не всякий университет мог научить этой премудрости. Нужно было непременно 
ехать в Италию: тамошние математики добились большого искусства в делении. Если 
напомнить, что в те времена пользовались непозиционной (римской) системой счисления, 
станет ясно, почему деление миллионных чисел было доступно лишь бородатым мужам, 
посвятившим этому всю свою жизнь.
С введением позиционной системы счисления все изменилось. В IX веке узбекский 
математик Мухаммед ибн Муса ал­Хорезми («ал­Хорезми» означает «Хорезмиец») описал 
правила выполнения четырех арифметических действий в десятичной системе счисления. 
Новые правила были значительно проще и сейчас ими владеют уже школьники младших 
классов. Поразительная простота указанных правил стимулировала их повсеместное 
распространение. Эти правила были изложены Мухаммедом в книге по математике, 
изданной в 825 году, где, кроме того, приводились многочисленные рецепты решения 
различных задач.
По латинским переложениям арифметического трактата ал­Хорезми средневековая Европа
знакомилась с индийской позиционной системой счисления и с искусством счета в этой 
системе. При переводе имя автора переделали в Алгоритми. Ссылки на рецепты решений 
из книги Мухаммеда европейские авторы начинали со слов: «Так говорил Алгоритми …». С 
течением времени сами рецепты для решения математических задач стали называть 
алгоритмами.
Первоначально под алгоритмами понимали только правила выполнения четырех 
арифметических действий над десятичными числами. В дальнейшем это понятие стали 
использовать для обозначения любой последовательности действий, приводящей к 
решению поставленной задачи.
Для разъяснения интуитивного понятия алгоритма рассмотрим несколько примеров.
В качестве первого примера рассмотрим один из самых древних и самых известных 
математических алгоритмов ­ алгоритм нахождения наибольшего общего делителя двух натуральных чисел. Этот алгоритм еще в III веке до нашей эры изложил (в геометрической 
форме) греческий ученый Евклид в теоретическом трактате по математике «Начала». 
Поэтому он носит название алгоритма Евклида. Алгоритм Евклида обсуждается 
практически в каждой книге по программированию.
Пример 1.1. Вычисление наибольшего общего делителя двух натуральных чисел m и n.
Составим алгоритм решения этой задачи в предположении, что его исполнителем будет 
некоторое вычислительное устройство.
Алгоритм Евклида
1. Поместить в участок памяти с именем x число m; перейти к выполнению пункта 2.
2. Поместить в участок памяти с именем y число n; перейти к выполнению пункта 3.
З. Если выполняется условие 
выполнению пункта 4.
, то перейти к выполнению пункта 5, иначе перейти к 
4. Поместить в участок памяти с именем НОД значение из блока памяти x; перейти к 
выполнению пункта 8.
5. Если выполняется условие x > y, то перейти к выполнению пункта 6, иначе перейти к 
выполнению пункта 7;
6. Поместить в участок памяти с именем x значение выражения x ­ y; перейти к выполнению
пункта 3.
7. Поместить в участок памяти с именем y значение выражения y ­ x; перейти к выполнению
пункта 3.
8. Закончить работу.
Внимательное рассмотрение алгоритма Евклида показывает, что запись алгоритма 
распадается на отдельные команды. Каждая команда снабжена номером и представляет 
собой указание исполнителю выполнить некоторое законченное действие. Исполнение 
алгоритма начинается с команды, имеющей номер 1. Далее команды выполняются в 
соответствии с указаниями, сопровождающими каждую команду алгоритма.
Для удобства ссылок, алгоритм обычно снабжается названием. В случае, когда для 
алгоритма не указывается специальное название, его названием обычно считают весь текст 
задачи, для решения которой этот алгоритм предназначен. Существует правило, согласно которому, при отсутствии специального указания 
следующей за данной командой должна выполняться команда, номер которой на единицу 
больше данной. Такая последовательность выполнения команд называется естественной. 
По указанию «кончить работу» исполнение алгоритма прекращается.
Пример 1.2. Умножение натуральных чисел столбиком [2].
1. Записать множимое.
2. Подписать множитель под множимым так, чтобы разряды множителя находились под 
соответствующими разрядами множимого.
3. Провести черту под множителем (под ней будут записываться частные суммы).
4. Взять очередную цифру множителя, начиная с единиц.
5. Если очередная цифра множителя равна нулю, пропустить ее и перейти к пункту 7.
6. Если очередная цифра не равна нулю, умножить на нее множимое и произведение как 
очередную частную сумму, подписать под чертой или под предыдущей частной суммой 
так, чтобы единицы произведения находились бы под очередной цифрой множителя.
7. Если очередная цифра не была последней, перейти к пункту 4.
8. Если очередная цифра оказалась последней, сложить частные суммы столбиком и общую
сумму взять в качестве искомого произведения.
Пример 1.3. Инструкция по приготовлению проявителя. Содержимое большого пакета 
растворить в 300 мл. воды при температуре I8­20° C; затем добавить содержимое малого 
пакета. Объем раствора довести до 500 мл. Раствор профильтровать.
В этом примере команды не пронумерованы. Все команды записаны последовательно, в 
виде сплошного текста. Друг от друга команды разделены либо точкой, либо точкой с 
запятой. При таком оформлении алгоритма исполнитель выполняет команды в порядке их 
естественного следования в тексте.
Такая форма записи алгоритма часто используется во всякого рода инструкциях, правилах,
рецептах и т.п. Она хороша в случае, когда алгоритм небольшой и когда для описания 
алгоритма отводится мало места. Недостатком такого оформления является его малая 
наглядность .
Упражнения
1.1. Составьте алгоритм сложения столбиком двух натуральных чисел. 1.2. Опишите правила перехода улицы для случаев:
а) перекресток регулируемый;
б) перекресток нерегулируемый (т.е. без светофора).
1.3. Опишите способ измерения длинной рейки с помощью линейки.
1.4. Укажите метод отыскания слова в орфографическом словаре.
1.5. Укажите алгоритм проведения перпендикуляра к прямой l, в заданной точке D.
1.6. Опишите несколько алгоритмов решения задач на следующие темы:
а) рецепты приготовления пищи (один из способов получения таких рецептов ­ 
воспользуйтесь поваренной книгой);
б) правила этикета (например, правило знакомства, алгоритм приветствия и т.п.);
в) правила дорожного движения;
г) правила поведения в бытовых ситуациях (алгоритм пользования газовой плитой, правило
пользования телефоном­автоматом и т.п.).
2. Свойства алгоритмов
Рассмотренные примеры показывают, что выполнение алгоритма разбивается на 
последовательность законченных действий­шагов. Каждое действие должно быть закончено
исполнителем прежде, чем он приступит к исполнению следующего действия. Это свойство
алгоритма называется дискретностью.
Произвести каждое отдельное действие исполнителю предписывает специальное указание в
записи алгоритма, называемое командой.
Запись алгоритма должна быть такой, чтобы на каждом шаге его выполнения было 
известно, какую команду надо выполнить следующей. Это свойство алгоритма 
называется точностью.
Алгоритм может быть выполнен только исполнителем, который понимает каждую команду
алгоритма и может ее исполнить в строгом соответствии с ее назначением. Это свойство 
называетсяпонятностью (для данного исполнителя).
­ Да пойми же, гайками прикрепляется рельса к шпалам!
­ Это мы понимаем… А. Чехов «Злоумышленник»
Будучи понятным, алгоритм не должен все же содержать предписаний, смысл которых 
может восприниматься неоднозначно. Это означает, что одно и то же предписание после 
исполнения должно давать один и тот же результат.
В данном случае речь фактически идет о том, что запись алгоритма должна быть настолько
четкой, настолько полной и продуманной в деталях, чтобы у исполнителя никогда не могло
возникать потребности в принятии каких­либо самостоятельных решений, не 
предусмотренных составителем алгоритма. Говоря иначе, алгоритм не должен оставлять 
места, для произвола исполнителя.
Отмеченное свойство называется свойством определенности, или детерминированности.
Замечание. Часто под свойством детерминированности алгоритма понимается 
одновременное выполнение свойств точности и понятности.
Важным свойством алгоритма является свойство результативности. Смысл этого 
свойства состоит в том, что при точном исполнении команд алгоритма процесс должен 
прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос 
задачи. В качестве одного из возможных ответов может быть и установление того факта, 
что задача решений не имеет.
Считается, что алгоритм наиболее интересен, если он, кроме того, обладает 
свойством массовости, т.е. пригодности для решения любой задачи из некоторого класса 
задач. Это свойство не следует понимать как возможность решить много задач. Свойство 
массовости предполагает, что заданный алгоритм позволяет решить любую задачу из 
определенного класса, причем этот класс может состоять и только из одной задачи.
Проиллюстрируем свойства алгоритма на примере алгоритма Евклида.
Массовость алгоритма Евклида заключается в том, что его можно применить к любой паре 
натуральных чисел. Результативность его состоит в том, что он определяет процесс, 
приводящий для любой пары натуральных чисел к получению их наибольшего делителя. 
Понятность алгоритма заключается в том, что исполнитель умеет выполнять действия, 
определяемые командами алгоритма. Детерминированность алгоритма вытекает из того, 
что каждая команда выполняется исполнителем однозначно. Точность алгоритма 
обеспечивается тем, что, во­первых, исполнителю известно, с чего начинать выполнение 
алгоритма (с команды номер 1), и, во­вторых, каждая команда снабжена указанием, какую 
команду выполнять следующей. Рис.2.1. Непонятное предписание
Очевидно, не каждое правило, приводящее к решению задачи, является алгоритмом. 
Разберем с этих позиций несколько таких правил.
Пример 2.1. Проведение перпендикуляра к прямой MN в заданной точке A [2].
I. Отложить в обе стороны от точки A на прямой MN циркулем отрезки равной длины с 
концами B и C,
2. Увеличить раствор циркуля до радиуса, в полтора­два раза большего длины 
отрезков AB в AC.
3. Провести указанным раствором циркуля последовательно с центрами B и C дуги 
окружностей так, чтобы они охватили точку A и образовали две точки пересечения друг с 
другом D и E.
4. Взять линейку и приложить ее к точкам D и E и соединить их отрезком. При правильном 
построении отрезок пройдет через точку А и будет искомым перпендикуляром
Рис. 2.2. Проведение перпендикуляра к прямой в заданной точке
Указанное правило, очевидно, рассчитано на исполнителя­человека. Применяя его, 
человек, разумеется, построит искомый перпендикуляр. Но, тем не менее, это правило 
алгоритмом не является.
Прежде всего, оно не обладает свойством детерминированности. Так, в пункте 1 требуется 
от исполнителя сделать выбор отрезка произвольной длины (для построения 
точек B и C надо провести окружность произвольного радиуса r с центром в точке A). В 
пункте 2 требуется сделать выбор отрезка в полтора­два раза большего длины 
отрезков AB и AC. В пункте 3 надо провести дуги, которые также однозначно не 
определяются их описанием. Человек­исполнитель, применяющий данное правило, к одним и тем же исходным данным (прямой MN и точке A) повторно, получит несовпадающие 
промежуточные результаты. Это противоречит требованию детерминированности 
алгоритма.
Попробуем переформулировать это правило, чтобы оно стало алгоритмом. Для этого 
следует во всех предписаниях избавить исполнителя от проблемы выбора.
Для этого мы вместо выбора произвольного радиуса будем указывать в каждом случае 
конкретный. Однако, этим неопределенность команд полностью не снимается. В 
инструкциях 1 и 2, кроме проведения окружностей, требуется находить точки пересечения 
и как­то их обозначать. Разберем возникающие при этом проблемы.
В команде 2 требуется присвоить имена точкам пересечения прямой MN и окружности 
. 
Здесь можно договориться обозначать точки, например, так, чтобы векторы 
были сонаправлены.
 и 
 
В команде 3 требуется обозначить точки пересечения окружностей 
. Договоримся, например, обозначать через D ту из двух точек пересечения, которая 
находится левее, если смотреть из центра B в направлении центра C.
 и 
Кроме того, вместо дуг окружностей в пункте 3, мы будем проводить окружности, ибо тем 
самым снимается неопределенность инструкции «провести дугу, охватывающую точку».
С учетом сказанного искомый алгоритм может выглядеть следующим образом.
Пример 2.2. Алгоритм проведения перпендикуляра к прямой MN в заданной точке A (
).
1. Провести окружность 
 радиуса 1 с центром в точке A.
2. Обозначить точки пересечения окружности 
 с прямой MN через B и C так, 
чтобы 
.
3. Последовательно провести окружности 
точках B и C.
 и 
 радиуса 2 с центром соответственно в 
 через D и E так, чтобы обход 
4. Обозначить точки пересечения окружностей 
многоугольника BDCE (последовательно от B через D и C к E) совершался по часовой 
стрелке.
 и 5. Провести прямую DE. Прямая DE ­ искомый перпендикуляр.
Рис.2.3. Проведение перпендикуляра к прямой в заданной точке 
В школьном учебнике [1] приведен алгоритм нахождения середины отрезка при помощи 
циркуля и линейки. В нем использован другой прием избавления от неопределенности 
инструкций при геометрических построениях.
Замечание. Подробное обсуждение вопросов, связанных с алгоритмами построения 
циркулем и линейкой, проводится в [3]. Всем, изучающим информатику, полезно 
познакомиться с этой интересной книгой.
3. Уточнение понятия алгоритма
«То, что вообще может быть сказано, может быть сказано ясно, а о чем невозможно
говорить ­ о том следует молчать».
Людвиг Витгенштейн (Эпиграф, предпосланный изложению языка программирования 
АЛГОЛ­60.)
Точное математическое определение понятия «алгоритм» было выработано лишь в 
тридцатых годах XX века. Почему же до этого времени математики довольствовались 
интуитивным понятием алгоритма? Это связано с тем, что обычно понятие алгоритма 
встречалось в связи с конкретным решением задачи. Об алгоритме говорили лишь тогда, 
когда предлагался способ решения какого­либо класса задач. В начале XX века в 
математике накопилось большое количество задач, которые не поддавались решению, 
несмотря на то, что над ними думали первоклассные ученые. Возникло подозрение, что для
некоторых из этих задач вообще не существует разрешающего алгоритма. Утверждение о 
неразрешимости того или иного класса задач можно было вывести, только имея точное 
определение алгоритма, надо было знать, несуществование чего требуется доказать.
Попытки дать строгое математическое определение алгоритма, согласующееся с 
интуитивным представлением об алгоритме, привели к выработке сразу нескольких 
определений (Черч, Пост, Тьюринг, Марков и др.). Впоследствии выяснилось, что все эти 
определения равносильны между собой и, следовательно, определяют одно и то же 
понятие.В качестве основы для уточнения понятия алгоритма мы выбираем так называемые машины с неограниченными регистрами, или, короче, МНР [4]. Изложение на базе МНР 
привлекательно ввиду близости этих машин к реальным ЭВМ.
Каждый алгоритм имеет дело с данными ­ входными, промежуточными и выходными. 
Поскольку мы собираемся уточнять понятие алгоритма, нужно уточнить и понятие данных.
В качестве данных для МНР мы ограничиваемся множеством Z0 неотрицательных целых 
чисел. Такое ограничение не является существенным, поскольку другие виды объектов и 
операции над ними могут быть закодированы натуральными числами и представлены как 
операции над натуральными числами.
Ниже мы перечислим все команды из списка предписаний МНР (для уточнения свойства 
«понятность»), однозначно определим действие каждой команды (для уточнения свойства 
«определенность») и опишем механизм реализации алгоритма (для уточнения свойства 
«точность»).
Машина с неограниченными регистрами является исполнителем, представляющим собой 
простой «идеализированный компьютер». Идеализация состоит в том, что каждый 
отдельный реальный компьютер ограничен как величиной чисел, которые поступают на 
вход, так и размером памяти (необходимой для запоминания промежуточных результатов),
МНР лишена этих ограничений. Машина с неограниченными регистрами имеет 
неограниченно большую память, ячейки которой будем называть регистрами и 
обозначать 
неотрицательное целое число. 
 Каждый регистр в любой момент времени содержит 
…
…
Рис. 3.1. Регистры МНР 
При этом только конечное множество регистров содержит числа, отличные от нуля. Все 
остальные регистры заполнены нулями. Это допущение предполагает, что каждый 
алгоритм использует только конечный объем памяти.
В список предписаний МНР входит четыре команды: команда обнуления Z(n); команда 
прибавления единицы S(n); команда переадресации T(m, n) и команда условного 
переходам J(m, n, q). Команды обнуления, прибавления единицы и переадресации 
называются арифметическими.
Обозначение  Действие, производимое МНР команды
по данной команде
Z(n)
S(n)
T(m, n)
J(m, n, q)
, то перейти к 
Если 
вычислению команды алгоритма 
с номером q.
Рис. 3.2. Список предписаний МНР
Алгоритмом называется конечная непустая последовательность команд из списка 
предписаний МНР, начинающаяся с команды с номером 1.
Производя вычисления по данному алгоритму, МНР изменяет содержимое регистров 
памяти в точном соответствии с командами алгоритма. Исходное состояние памяти, то 
есть последовательность чисел 
вычислений, называется начальной конфигурацией.
 в регистрах 
 перед началом 
Предположим, что некоторый алгоритм P состоит из последовательности 
команд I1, I2, …, Is. МНР начинает вычисление с команды I1, затем выполняются 
команды I2, I3 и т. д. до тех пор, пока не встретится команда вида J(m, n, q). В этом случае 
МНР переходит к выполнению команды, предписанной J(m, n, q) и текущим содержанием 
регистров Rm и Rn
Пример 3.2. Рассмотрим алгоритм P1
I1
I2
I3
I4
I5
I6
J(1, 2, 6)
S(2)
S(3)
J(1, 2, 6)
J(1, 1, 2)
T(3, 1)
Применим алгоритм к следующей начальной конфигурации: R1
5
R2
3
R3
0
R4
0
R5
0
…
…
Рис. 3.3. Начальная конфигурация 
Ход вычисления на МНР по алгоритму P1 с начальной конфигурацией, изображенной на 
рисунке 3.3, можно представить, записывая последовательно сверху вниз конфигурации 
машины вместе со следующей командой, к которой она переходит на данном шаге. 
R1
R2
R3
R4
R5
5
5
5
5
5
5
5
5
5
2
3
3
4
4
4
4
5
5
5
5
0
0
0
1
1
1
1
2
2
2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
…
…
…
…
…
…
…
…
…
…
…
 
 
 
 
 
 
 
 
 
 
 
Рис. 3.4. Вычисление по алгоритму P1 
Следующая команда
I1
I2
I3
I4
I5
I2
I3
I4
I6
I7
 
(так как R1  R2)
 
 
(так как R1  R2)
(так как R1 = R2)
 
 
(так как R1 = R2)
 
МНР выполняет алгоритм P: I1, I2, …, Is до тех пор, пока это возможно. Вычисление 
останавливается тогда и только тогда, когда нет следующей команды, то есть когда МНР 
только что выполнила команду Ik и следующая команда в вычислении есть Iv, где v > s. Это 
может произойти одним из способов:
I) если Ik = Is (выполнена последняя команда в P) и Ik ­ арифметическая команда;
2) если Ik = J(m, n, q), Rm = Rn и q > s.
3) если Ik = J(m, n, q), Rm Rn и q = s. В этом случае будем говорить, что вычисление остановилось после выполнения команды Ik,
и заключительная конфигурации есть последовательность r1, r2, r3, … содержимого 
регистров на этом шаге.
Результатом применения алгоритма к некоторой начальной конфигурации будем считать 
число r1 из регистра R1 заключительной конфигурации.
Бывают, конечно, вычисления, которые никогда не заканчиваются, например, никогда не 
заканчивается ни при какой начальной конфигурации вычисление по алгоритму:
I1
I2
S(1)
J(1, 1, 1)
В случае, если вычислительный процесс не заканчивается получением результата, говорят, 
что алгоритм неприменим к начальной конфигурации. 
Упражнение
1. Покажите, что вычисление по алгоритму из примера 6 с начальной конфигурацией 6, 
7, 0, 0, 0, … никогда не остановится.
Для удобства обозначим через P(a1, a2, …, an) вычисление по алгоритму P с начальной 
конфигурацией
a1, a2, …, an, 0, 0, …. Если вычислительный процесс заканчивается с результатом b, будем 
писать
P(a1, a2, …, an) = b.
Определение 3.1. Пусть f ­ функция от n неотрицательных целых переменных со 
значениями во множестве Z0 неотрицательных целых чисел (функция 
Функция f называетсявычислимой на МНР (или МНР­вычислимой), если существует такой
алгоритм P, что
). 
1) вычисление P(a1, a2, …, an) останавливается тогда и только тогда, когда (a1, a2, …, an) 
принадлежит области определения f;
2) если (a1, a2, …, an) принадлежит области определения f; то в заключительной 
конфигурации в регистре R1 находится целое число b такое, что f(a1, a2, …, an) = b.
С этого момента под термином вычислимое будем подразумевать МНР­вычислимое.
Рассмотрим теперь несколько простых примеров вычислимых функций. Пример 3.2. Докажите МНР­вычислимость функции x + y.
Решение. Получим x + y, прибавляя y раз 1 к числу x. Начальной конфигурацией алгоритма 
служит x, y, 0, 0, 0, …. Типичной конфигурацией в процессе вычисления является
R1
x + k
R2
y
R3
k
R4
0
R5
0
…
…
Определим алгоритм следующим образом:
I1
I2
I3
I4
J(3, 2, 5)
S(1)
S(3)
J(1, 1, 1)
Заданный алгоритм вычисляет функцию x + y.
Пример 3.3. Докажите МНР­вычислимость функции
Решение. Составим алгоритм для начальной конфигурации x, 0, 0, … . Типичной 
конфигурацией в процессе вычисления является:
R1
x
R2
k
R3
k + 1
R4
0
R5
0
…
…
Следующий алгоритм МНР­вычисляет функцию.
I1
I2
I3
I4
I5
I6
J(1, 2, 6)
S(2)
J(1, 2, 6)
S(3)
J(1, 1, 2)
T(3, 1)
Упражнения 3.2. Составьте алгоритмы, вычисляющие функции:
а) 
б) 
в) 
г) 
д)* 
е)* 
Здесь [x / y] означает наименьшее целое число, не превосходящее действительное число 
x / y.
3.3. Покажите, что для каждой команды переадресации существует программа без команд 
переадресации, которая на всякой конфигурации МНР дает тот же результат, что и T(m, n).
Это означает, что команды переадресации на самом деле избыточны в нашем определении 
МНР. Тем не менее, представляется естественным и удобным иметь такие команды, 
облегчающие построение алгоритмов.
Введем еще несколько понятий необходимых для дальнейшего изложения.
Определение 3.2. n­местным предикатом на множестве M называется отображение H, 
сопоставляющее каждому упорядоченному набору (a1, a2, …, an) элементов из M одно из 
логических значений «истинно» или «ложно».
Пример 3.4. Функции «быть простым числом», «быть четным числом» являются 
одноместными предикатами на множестве целых чисел.
Пример 3.5. Свойства «иметь одинаковые остатки при делении на 3» или «быть равными» 
являются бинарными предикатами на множестве целых чисел.
Определение 3.3. Предикат 
его характеристическая функция
 называется разрешимым, если вычислима.
В контексте вычислимости предикаты часто называют проблемами. Поэтому ниже мы 
наряду с термином «разрешимый предикат» будем использовать также «разрешимая 
проблема».
Упражнение
3.4. Докажите разрешимость следующих предикатов на множестве целых неотрицательных 
чисел:
а) x = y;
б) 
;
в) x < y;
г) x ­ четное число.
За последние пятьдесят лет было предложено много математических уточнений 
интуитивного понятия «алгоритм». Подход, основанный на МНР, является одним из них. 
Между этими подходами имеются большие различия, и в то же время все эти подходы 
эквивалентны между собой в том же смысле, что каждое уточнение алгоритма приводит к 
одному и тому же классу вычислимых функций.
Возникает теперь вопрос: насколько хорошо неформальное интуитивное понятие 
вычислимой функции отражено в различных формальных описаниях? Этот вопрос 
подвергался математиками серьезному обсуждению, в результате которого было высказано
утверждение, известное под названием «тезис Черча»: каждая функция, вычислимая 
посредством процесса, алгоритмический характер которого интуитивно ясен, является 
вычислимой функцией. Применительно к нашему изложению этот тезис можно 
перефразировать следующим образом: всякая функция, для которой существует алгоритм 
(в интуитивном смысле) вычисления ее значений, является МНР­вычислимой функцией.
Сразу же заметим, что это утверждение не является теоремой, подлежащей 
математическому доказательству; оно имеет статус утверждения, принимаемого как 
постулат, справедливость которого подтверждается рядом свидетельств. Во­первых, таким
свидетельством является то, что, как уже отмечалось, многие независимые уточнения 
интуитивного понятия вычислимой функции привели к одному и тому же классу функций. Во­вторых, никому не доводилось найти функцию, которую можно признать вычислимой в 
интуитивном смысле и которая не была бы МНР­вычислимой. Исходя из этих соображений
и собственного опыта, большинство математиков приняли тезис Черча.
4. Нумерация программ для МНР
Определение 4.1. Множество X называют счетным, если можно установить взаимно 
однозначное отображение 
чисел Z0 и множествомX.
 между множеством неотрицательных целых 
Определение 4.2. Множество называют не более чем счетным, если оно счетно или 
конечно.
Определение 4.3. Перечислением или нумерацией множества X называется 
отображение 
 множества Z0 на множество X.
Перечисление f определяет на множестве X некоторую бесконечную 
последовательность 
множества X встречается в этой последовательности, по крайней мере, один раз.
 элементов из X такую, что каждый из элементов
Если отображение f ­ взаимно однозначно, 
то f называют перечислением или нумерацией без повторений.
Определение 4.4. Множество X называется эффективно счетным, если существует 
функция 
множествами Z0 и Xтакая, что f и f­­1 ­ вычислимые функции.
, устанавливающая взаимно однозначное соответствие между 
Теорема 4.1. Следующие множества являются эффективно счетными:
а) 
б) 
в) 
;
;
 ­ множество всех конечных последовательностей целых неотрицательных чисел.
Доказательство. а) Докажем сначала эффективную счетность множества 
состоящего из упорядоченных пар (x, y) с целочисленными неотрицательными 
компонентами x и y.Геометрически это множество представляет целочисленную решетку 
(рис. 4.1).
, Рис. 4.1. Целочисленная решетка
Перенумеровать точки этой решетки можно различными способами, например, так, как 
показано на рисунке 4.2.
Рис. 4.2. Нумерация точек целочисленной решетки
Предложенная нумерация устанавливает взаимно однозначное 
отображение 
 между множествами 
 и 
. Алгоритмический 
характер процесса вычисления значений функции 
 очевиден. Следовательно, по 
тезису Черча 
 ­ вычислимая функция.
Для вычисления значений обратной функции 
предложенным алгоритмом последовательно нумеровать точки целочисленной решетки до 
 можно, например, в соответствии с номера z. Пара (x, y) координат точки с номером z является значением обратной 
функции 
. По тезису Черча 
 ­ вычислимая функция.
Таким образом, множество 
 эффективно счетно.
б) Теперь несложно доказать эффективную счетность множества 
. Для этого 
определим взаимно однозначное отображение 
 множества 
 упорядоченных 
троек неотрицательных целых чисел на множество 
 следующим 
образом 
. Из вычислимости функций 
 и 
 вытекает 
вычислимость функций 
 и 
. Поэтому множество 
 эффективно счетно.
в) Для доказательства эффективной счетности множества всех конечных 
последовательностей целых неотрицательных чисел 
 рассмотрим функцию 
, 
сопоставляющую каждому упорядоченному набору (a1, a2, …, ak) из k неотрицательных 
целых чисел некоторое неотрицательное целое число.
Для доказательства взаимной однозначности функции 
каждого целого числа имеется ровно одно представление в двоичной системе счисления. 
 используем тот факт, что у 
Запишем значение функции 
 в двоичной системе счисления:
Например,
= 
 = 616 ­ 1 = 615;
= 2320 ­1 = 2319;
 (*)
 = 
 = 
 = 544 ­1 = 543; = 520 ­ 1 = 519;
 = 3 ­ 1 = 2;
 = 32 ­ 1 = 31;
 = 1 ­ 1 = 0.
Однозначность отображения 
 следует из того, что
. 
Так как, кроме того, для любого неотрицательного числа x существует, очевидно, кортеж 
(c1, c2, …, cn) такой, что 
 устанавливает взаимно 
, то функция 
однозначное соответствие между множеством 
 и множеством 
.
Покажем, как вычисляются значения обратной функции 
неотрицательного числа x.
 для произвольного 
В соответствии с формулой (*)
где 
 ­ запись числа x + 1 в двоичной системе счисления.
Например,
,
;
;
;
;
; ;
.
;
В силу тезиса Черча функции 
вычислимое множество.
 и 
 вычислимы. Следовательно, 
 ­ эффективно 
Теорема 4.2. Множество K команд МНР эффективно счетно.
Доказательство. Множество K команд МНР включает четыре типа команд Z(n), S(n), T(m, 
. Определим взаимно однозначное отображение 
 
n), J(m, n, q), где 
следующим образом:
 = 4  (n ­ 1);
 = 4  (n ­ 1) + 1;
;
,
где 
 ­ отображения, определенные в теореме 4.1.
Так как функции 
счетность множества K команд МНР.
, очевидно, вычислимы, то отсюда вытекает эффективная 
Теорема 4.3. Множество P всех программ для МНР эффективно счетно.
Доказательство. Пусть 
 ­ произвольная программа для МНР. Определим 
взаимно однозначное отображение 
 следующим образом:
. 
­ отображения, определенные в теореме 4.1. Так как функции 
где 
очевидно, вычислимы, то отсюда вытекает эффективная счетность множества P всех 
программ для МНР.
, Разумеется, существует много других отображений из P в 
эффективную счетность множества P. Для нашего изложения подходит любое из таких 
отображений. Зафиксируем одно из них, например, то которое описано в теореме 4.3.
, устанавливающих 
Определение 4.5. Число (P) называется геделевым номером программы P или 
просто номером программы P.
Отображение играет важную роль в теории алгоритмов. Название числа (P) связано с 
именем К. Геделя, впервые в 1931 году предложившего идею кодирования нечисловых 
объектов натуральными числами.
Ниже программу P с геделевым номером n будем обозначать 
. Из взаимной 
однозначности отображения следует 
могут вычислять одну и ту же функцию.
 при 
, хотя обе эти программы 
 и 
 
Пример 4.1. Найдем геделев номер программы P:
,
,
вычисляющей функцию f(x) = x + 2.
(S(1)) = 4  (1 ­ 1) + 1 = 1;
.
.
Пример 4.2. Вычислим программу 
 по ее геделеву номеру m.
1) m = 0.
; 
.
Следовательно,
: 1. Z(1).
2) m = 1. .
; 
.
Следовательно,
: 1. S(1).
3) m = 2.
; 
Следовательно,
: 1. Z(1),
2. Z(1).
4) m = 3.
; 
.
Следовательно,
: 1. T(1, 1).
Заметим, что различные программы 
 и 
 вычисляют одну и ту же функцию f(x) = 0. 
5. Нумерация вычислимых функций
Определение 5.1. Пусть f ­ n­местная функция, вычислимая по программе P с геделевым 
номером m = (P). Число m будем называть индексом функции f. Вычислимую функцию 
от n переменных с индексом m будем обозначать символом 
.
Из определения 5.1 следует, что каждая n­местная вычислимая функция f представлена в 
перечислении 
Ниже мы в основном будем рассматривать одноместные вычислимые функции 
простоты в их обозначении верхний индекс будем опускать.
. Для 
Упражнение
5.1. Докажите, что у каждой вычислимой функции имеется бесконечно много индексов. Приступим теперь к доказательству теоремы о существовании невычислимых функций. 
Идея доказательства этой теоремы столь же важна, как и результат.
Теорема 5.1. Существует невычислимая всюду определенная функция.
Доказательство. Пусть 
 ­ некоторое перечисление всех вычислимых функций:
Положим
Функция g отличается от любой вычислимой функции 
 в точке n. Действительно, если 
функция 
 определена в точке n, то 
. Если 
 не определена в точке n, 
то g отличается от 
следовательно, g ­ невычислимая всюду определенная функция.
 тем, что значение g(n) определено. Таким образом, 
 и, 
Метод построения функции в теореме 5.1 является примером диагональной конструкции, 
открытой Кантором. Лежащая в его основе идея является центральной в доказательстве 
большинства результатов, связанных с вычислимостью функций, и применима к огромному 
числу ситуаций, возникающих в различных разделах математики.
Поясним, почему для примененного в теореме 5.1 метода выбран термин диагональный. 
Для этого проиллюстрируем метод построения функции g с помощью следующей 
бесконечной таблицы:
 
0
1
2
3
…
…
…
…
…
Рис. 5.1. Диагональная конструкция
…
…
…
…
…
… При построении функции g для определения значений в точках n выбирались диагональные
элементы таблицы 
. Выбранные значения изменялись так, чтобы 
обеспечить отличие g(n) от 
.
Очевидно, что новые значения функции можно выбирать сравнительно свободно. 
Например, функция 
является другой невычислимой всюду определенной функцией.
Проиллюстрируем диагональную конструкцию на примере из теории множеств.
Пример 5.1. Докажем, что множество всех подмножеств множества 
(перенумеровать).
 нельзя перечислить 
От противного, пусть 
 ­ перечисление всех подмножеств множества 
. 
Определим новое подмножество B множества 
 следующим образом:
.
Очевидно, 
, что противоречит предположению. 
Поэтому множество всех подмножеств множества 
 нельзя перечислить.
Из доказанного вытекает, что множество всех подмножеств множества 
 несчетно.
Упражнения
5.2. Используя диагональный метод, докажите что множество всех функций 
из N в N несчетно (Кантор).
5.3. Докажите, что множество всех невычислимых всюду определенных функций 
из N в N несчетно.
6. Универсальные программы
В этом разделе мы докажем несколько неожиданный результат, состоящий в том, что 
существуют универсальные программы, то есть программы, которые в некотором смысле реализуют все другие программы. Этот результат является одним из основных результатов 
теории вычислимости.
Определение 6.1. Универсальной функцией для n­местных вычислимых 
функций называется (n+1)­местная функция 
. 
Для примера рассмотрим функцию 
. Эта функция реализует все одноместные 
вычислимые функции 
. Действительно, для произвольного неотрицательного 
целого числа тфункция 
 совпадает с функцией 
. Таким образом, 
название функции 
функций.
 вполне соответствует классу вычисляемых ею одноместных 
Ниже для простоты вместо 
 будем писать 
.
Теорема 6.1. Для каждого натурального числа n универсальная функция 
 вычислима.
Доказательство. Покажем, как можно вычислить значение функции 
заданного числа m и фиксированного набора (x1, …, xn). Неформальная процедура 
 для 
вычисления значения 
восстановите программу Рm. Затем имитируйте вычисление по этой программе. Если 
 состоит в следующем: «Декодируйте число m и 
вычисление по программе заканчивается, требуемое значение 
 содержится
в регистре R1». По тезису Черча заключаем, что функция 
 вычислима.
Определение 6.2. Любая программа Р(n), вычисляющая функцию 
называется универсальной программой.
, 
Универсальные программы полностью соответствуют своему названию. Действительно, так
как универсальная программа Р(n) позволяет вычислить любую n­местную вычислимую 
функцию, то, по сути дела, программа Р(n) заменяет абсолютно все программы для 
вычисления n­местных функций.
Проиллюстрируем теперь, как использовать вычислимость универсальных функций в 
диагональных построениях. 7. Алгоритмически неразрешимые проблемы
Основным стимулом, приведшим к выработке понятия алгоритма и созданию теории 
алгоритмов, явилась потребность доказательства неразрешимости многих проблем, 
возникших в различных областях математики. Специалист, решая задачу, всегда должен 
считаться с возможностью того, что она может оказаться неразрешимой.
При доказательстве неразрешимости той или иной проблемы часто используется так 
называемый метод сводимости, заключающийся в следующем. Пусть, например, в 
результате некоторых рассуждений удалось показать, что решение проблемы Pr1 приводит 
к решению другой проблемы Pr2. В этом случае говорят, что проблема Pr2 сводится к 
проблеме Pr1. Таким образом, если проблема Pr2 сводится к проблеме Pr1, то из 
разрешимости Pr1 следует разрешимость Pr2 и, наоборот, из неразрешимости Pr2 следует 
неразрешимость Pr1. В данном разделе метод сводимости используется при доказательстве
теоремы 7.3.
Ниже доказывается неразрешимость ряда известных проблем.
Теорема 7.1. Проблема «функция 
 всюду определена» неразрешима.
Доказательство. Пусть g ­ характеристическая функция этой проблемы
Нам надо показать, что функция g невычислима.
От противного, предположим, что g ­ вычислимая функция. Рассмотрим функцию
Функция f всюду определена и отличается от каждой вычислимой функции 
.
Применяя g и универсальную функцию 
, запишем f в виде:
Из вычислимости функций g и 
 по тезису Черча следует вычислимость функции f. Полученное противоречие доказывает невычислимость функции g. Таким образом, 
проблема «функция 
 всюду определена» неразрешима.
Обозначим область определения 
 и множество значений 
 функции 
 
через 
 и 
 соответственно.
Теорема 7.2. Проблема »
» неразрешима.
Доказательство. Характеристическая функция этой проблемы задается следующим 
образом:
Предположим, что функция g вычислима, и приведем это предположение к противоречию.
Рассмотрим функцию
Так как функция g вычислима, то по тезису Черча функция f также вычислима. С другой 
стороны, для любого x область определения Dom(f) функции f отлична от области 
определения 
, и, следовательно, 
.
Таким образом, предположение о вычислимости характеристической функции g неверно. 
Поэтому проблема »
» неразрешима.
Замечание 7.1. Доказанная теорема вовсе не утверждает, что мы не можем для любого 
конкретного числа a сказать, будет ли определено значение 
утверждается, что не существует единого общего метода решения вопроса о том, будет ли 
. В теореме лишь 
значение 
 определено.
Замечание 7.2. Проблему »
» называют также проблемой самоприменимости. Такое 
название связано с формулировкой проблемы в форме: «Остановится ли МНР, работая по 
программе 
программа к своему кодовому номеру?».
 с начальной конфигурацией (x)?». Другими словами: «Применима ли Теорема 7.3. Проблема »
» неразрешима.
Доказательство. Если бы проблема »
» была разрешима, то была бы разрешима более 
простая проблема »
«, что противоречит доказанной выше теореме.
Замечание 7.3. Доказанную теорему часто интерпретируют как утверждение о 
неразрешимости проблемы остановки, в которой говорится, что не существует общего 
метода, устанавливающего, остановится ли некоторая конкретная программа, запущенная с
некоторым конкретным набором начальных данных.
Смысл этого утверждения для теоретического программирования очевиден: не 
существует общего метода проверки программ на наличие в них бесконечных циклов.
В доказательстве теоремы мы показали, что проблема остановки »
«, по крайней 
мере, не проще, чем проблема самоприменимости »
«. Мы свели вопрос о 
неразрешимости одной проблемы к другой. Это прием часто используется при 
доказательстве неразрешимости проблем.
8. s­m­n­теорема
В этом разделе мы докажем теорему, принадлежащую к числу основных результатов 
теории алгоритмов. Суть теоремы в следующем. Допустим, что f(х, у) ­ вычислимая 
функция. Для каждого фиксированного значения a переменной х функция f порождает 
одноместную вычислимую функцию ga(y) = f(a, у). Из вычислимости функции ga следует 
существование индекса b такого, чтоf(a, у) = fb(у). Оказывается индекс b можно 
эффективно вычислить по параметру а.
Теорема 8.1 (s­m­n­теорема, простая форма). Пусть f(х, у) ­вычислимая функция. 
Существует всюду определенная вычислимая функция s(x), такая, что f(х, у) = fs(x)(у).
Доказательство. Из вычислимости функции f(х, у) следует существование МНР­
программы Pr, которая, исходя из начальной конфигурации (x, y, 0, 0, …), вычисляет 
значение функции f от двух аргументов х и у. Изменим программу Pr, добавив спереди 
команды, преобразующие начальную конфигурацию 
R1
y
R2
0
R3
0
R4
0
…
…
 
 
 
(*)
в конфигурацию R1
a
R2
y
R3
0
R4
0
…
…
 
 
следующим образом:
T(1, 2)
Z(1)
Pr
Новая программа Pr1, примененная к начальной конфигурации (*), вычисляет значение 
функции ga(y) = f(a, у) от одного аргумента у.
Теперь рассмотрим функцию s(a) = (Pr1), сопоставляющую произвольному 
неотрицательному целому числу a геделев номер программы Pr1. Функция s всюду 
определена и по тезису Черча вычислима. Кроме того, по построению fs(a)(у) = f(a, у) для 
каждого 
.
Замечание 8.1. Сформулированную теорему называют также теоремой параметризации, 
поскольку она позволяет по заданной вычислимой функции f(x, у) и фиксированному 
параметру a найти геделев номер s(a) программы, вычисляющей функцию fs(a)(у) = f(a, у).
Доказанная выше теорема 8.1 является частным случаем более общей теоремы.
Теорема 8.2 (s­m­n­теорема). Пусть m, n ­ натуральные числа, 
вычислимая функция с геделевым номером a. Существует всюду определенная вычислимая
 ­ 
функция 
 такая, что 
. 
Доказательство сформулированного утверждения аналогично доказательству теоремы 8.1.
Замечание 8.2. Название теоремы 8.2 связано с обозначением 
формулировке теоремы.
 для функций в Покажем теперь, как можно использовать s­m­n­теорему для доказательства 
неразрешимости проблем. s­m­n­теорема часто используется для сведения проблемы »
» к другим проблемам.
Теорема 8.3. Проблема »
» неразрешима.
Доказательство. Рассмотрим функцию 
По тезису Черча функция f(x, y) вычислима. Отсюда по s­m­n­теореме вытекает 
существование всюду определенной вычислимой функции s(x) такой, что 
По определению функции f(x, y) имеем:
. 
.
Следовательно, истинность условия 
 можно установить, определив справедливость 
равенства 
Поскольку первая из них неразрешима, то неразрешима и вторая.
. Тем самым мы свели проблему »
» к проблеме »
«. 
Замечание 8.3. Теорема 8.3 показывает, что в области проверки правильности 
компьютерных программ имеются принципиальные ограничения. В ней говорится о том, 
что не существует алгоритма проверки того, будет ли программа вычислять нулевую 
функцию. Несколько изменив доказательство теоремы 8.3, можно убедиться в том, что то 
же самое справедливо и для любой другой конкретной вычислимой функции.
Теорема 8.4. Проблема 
 неразрешима.
Доказательство. Допустим, что проблема 
 разрешима. Тогда разрешима и 
проблема 
, где c ­ индекс функции 0 
. Однако, это противоречит теореме 
8.3. Таким образом, проблема 
 неразрешима.
Замечание 8.4. Из теоремы 8.4 следует, что вопрос о том, вычисляют ли две программы 
одну и ту же одноместную функцию, неразрешим. Важность этого результата для 
теоретического программирования очевидна.
Упражнения 8.1. Докажите, что не существует алгоритма, определяющего по тексту программы, будет 
ли эта программа вычислять некоторую конкретную вычислимую функцию.
8.2. 2. Покажите, что не существует всюду определенной вычислимой функции f(x, y), 
обладающей следующим свойством: если программа 
происходит за f(x, y)или меньше шагов.
 останавливается, то это 
Указание. Покажите, что если бы такая функция существовала, то проблема остановки 
была бы разрешима.
Естественно задаться вопросом, какие свойства вычислимых функций можно 
алгоритмически распознать по их программам. Оказывается, что никакие, кроме 
тривиальных. Доказательство этого факта содержится в теореме Райса.
Теорема 8.5 (теорема Райса). Пусть B ­ непустое множество одноместных вычислимых 
функций, не совпадающее со всем множеством 
 одноместных вычислимых функций. 
Тогда проблема »
» неразрешима.
Доказательство. Очевидно, что проблема »
» разрешима тогда и только тогда, когда 
разрешима проблема »
«. Поэтому без потери общности можно считать, что нигде
не определенная функция 
 не принадлежит B.
Выберем некоторую функцию 
 и рассмотрим функцию 
По тезису Черча функция f(x, y) вычислима. Поэтому существует (по s­m­n­теореме) всюду
определенная вычислимая функция s(x) такая, что 
функцииf(x, y) имеем:
. По определению 
. 
Таким образом, с помощью вычислимой функции s(x) мы свели проблему »
» к 
проблеме »
«. Следовательно, проблема »
» неразрешима. Дадим более содержательную формулировку теоремы Райса. Пусть Q некоторое свойство 
одноместных вычислимых функций. Свойство Q назовем нетривиальным, если 
существуют функции, обладающие свойством Q, и функции не обладающие этим 
свойством.
Все обычно рассматриваемые свойства являются нетривиальными. Примерами 
нетривиальных свойств служат следующие:
 функция тождественно равна нулю;
 функция нигде не определена;
 функция всюду определена;
 функция взаимно однозначна;
 функция определена при x = 0.
Так как вычислимые функции могут быть заданы программами их вычисления, то 
естественно возникает вопрос: можно ли по программе узнать, обладает ли 
соответствующая ей функция заданным нетривиальным свойством.
Теорема 8.6. Каково бы ни было нетривиальное свойство Q одноместных вычислимых 
функций, задача распознавания этого свойства алгоритмически неразрешима.
Доказательство. Пусть B ­ множество одноместных вычислимых функций, обладающих 
свойством Q. Множество B не пусто и не совпадает со всем множеством одноместных 
вычислимых функций. По теореме Райса проблема »
» неразрешима.
Из последней теоремы следует неразрешимость многих задач, связанных с 
программированием. Например, если имеется некоторая программа, то по ней, вообще 
говоря, ничего нельзя сказать о функции, реализуемой программой. По двум программам 
нельзя установить, реализуют ли они одну и ту же функцию, а это приводит к 
неразрешимости многих задач, связанных с эквивалентными преобразованиями и 
минимизацией программ. В любом алгоритмическом языке, какие бы правила синтаксиса 
там ни применялись, всегда будут иметься «бессмысленные» программы, задающие 
функции не определенные ни в одной из точек (эти программы нельзя обнаружить). 
Теорема Райса позволяет доказывать алгоритмическую неразрешимость многих задач, 
связанных с вычислениями на компьютерах.
Более подробно ознакомиться с формальными подходами к вычислимости можно по 
книгам [4, 5]. ЛИТЕРАТУРА
1. Основы информатики и вычислительной техники. Пробное учебное пособие для средних 
учебных заведений. Ч. 1. Под ред. А. П. Ершова и В. М. Монахова. ­ М: Просвещение, 1985.
2. Ершов А. П. Алгоритмический язык . ­ Наука и жизнь. ­ 1985. ­ №11. ­ С. 61­63.
3. Абрамов С. А. Математические построения и программирование. ­ М.: Наука, 1978.
4. Катленд Н. Вычислимость. Введение в теорию рекурсивных функций. ­ М.: Мир, 1983.
5. Трахтенброт В. Л. Алгоритмы и вычислительные автоматы. ­ М.: Советское радио, 1974.
INTRODUCTION IN THE THEORY OF ALGORITHMS 
E. P. Emelchenkov,  V. E. Emelchenkov 
Понятие алгоритма. Свойства алгоритма. Исполнители алгоритмов (назначение, 
среда, режим работы, система команд). Компьютер как формальный исполнитель 
алгоритмов (программ).
Появление алгоритмов связывают с зарождением математики. Более 1000 лет назад (в 825 
году) ученый из города Хорезма Абдулла (или Абу Джафар) Мухаммед бен Муса аль­
Хорезми создал книгу по математике, в которой описал способы выполнения 
арифметических действий над многозначными числами. Само слово алгоритм возникло в 
Европе после перевода на латынь книги этого математика. Алгоритм – описание последовательности действий (план), строгое исполнение которых 
приводит к решению поставленной задачи за конечное число шагов.
Вы постоянно сталкиваетесь с этим понятием в различных сферах деятельности человека 
(кулинарные книги, инструкции по использованию различных приборов, правила решения 
математических задач…). Обычно мы выполняем привычные действия не задумываясь, 
механически. Например, вы хорошо знаете, как открывать ключом дверь. Однако, чтобы 
научить этому малыша, придется четко разъяснить и сами эти действия и порядок их 
выполнения:
1. Достать ключ из кармана.
2. Вставить ключ в замочную скважину.
3. Повернуть ключ два раза против часовой стрелки.
4. Вынуть ключ.
Если вы внимательно оглянитесь вокруг, то обнаружите множество алгоритмов которые 
мы с вами постоянно выполняем. Мир алгоритмов очень разнообразен. Несмотря на это, 
удается выделить общие свойства, которыми обладает любой алгоритм.
Свойства алгоритмов:
1. Дискретность (алгоритм должен состоять из конкретных действий, следующих в 
определенном порядке);
2. Детерминированность (любое действие должно быть строго и недвусмысленно 
определено в каждом случае);
3. Конечность (каждое действие и алгоритм в целом должны иметь возможность 
завершения);
4. Массовость (один и тот же алгоритм можно использовать с разными исходными 
данными);
5. Результативность (отсутствие ошибок, алгоритм должен приводить к правильному 
результату для всех допустимых входных значениях).
Виды алгоритмов:
1. Линейный алгоритм (описание действий, которые выполняются однократно в заданном 
порядке);
2. Циклический алгоритм (описание действий, которые должны повторятся указанное 
число раз или пока не выполнено задание);
3. Разветвляющий алгоритм (алгоритм, в котором в зависимости от условия выполняется 
либо одна, либо другая последовательность действий) 
4. Вспомогательный алгоритм (алгоритм, который можно использовать в других 
алгоритмах, указав только его имя). Для более наглядного представления алгоритма широко используется графическая форма
­ блок­схема, которая составляется из стандартных графических объектов.
Вид стандартного графического 
объекта
Назначение
Начало алгоритма
Конец алгоритма
Выполняемое действие 
записывается внутри 
прямоугольника
Условие выполнения действий 
записывается внутри ромба
Счетчик кол­во повторов
Последовательность выполнения 
действий.
Стадии создания алгоритма:
1. Алгоритм должен быть представлен в форме, понятной человеку, который его 
разрабатывает.
2. Алгоритм должен быть представлен в форме, понятной тому объекту (в том числе и 
человеку), который будет выполнять описанные в алгоритме действия.
Объект, который будет выполнять алгоритм, обычно называют исполнителем.
Исполнитель ­ объект, который выполняет алгоритм.
Идеальными исполнителями являются машины, роботы, компьютеры…
Исполнитель способен выполнить только ограниченное количество команд. Поэтому 
алгоритм разрабатывается и детализируется так, чтобы в нем присутствовали только те 
команды и конструкции, которые может выполнить исполнитель. Исполнитель, как и любой объект, находится в определенной среде и может выполнять 
только допустимые в нем действия. Если исполнитель встретит в алгоритме неизвестную 
ему команду, то выполнение алгоритма прекратится.
Компьютер – автоматический исполнитель алгоритмов.
Алгоритм, записанный на «понятном» компьютеру языке программирования, называется 
программой.
Программирование ­ процесс составления программы для компьютера. Для первых ЭВМ 
программы записывались в виде последовательности элементарных операций. Это была 
очень трудоемкая и неэффективная работа. Поэтому в последствии были разработанные 
специальные языки программирования. В настоящее время существует множество 
искусственных языков для составления программ. Однако, так и не удалось создать 
идеальный язык, который бы устроил бы всех.
 
Общее понятие алгоритма. Основные свойства алгоритма
Алгоpитм — точное и понятное пpедписание исполнителю совеpшить последовательность 
действий, направленных на решение поставленной задачи.
    Название «алгоритм» произошло от латинской формы имени среднеазиатского 
математика аль­Хорезми — Algorithmi. Алгоритм — одно из основных понятий 
информатики и математики.
    Основные свойства алгоритмов следующие:
1. Понятность для исполнителя — т.е. исполнитель алгоритма должен знать, как его 
выполнять.
2. Дискpетность (прерывность, раздельность) — т.е. алгоpитм должен пpедставлять 
пpоцесс pешения задачи как последовательное выполнение пpостых (или pанее 
опpеделенных) шагов (этапов).
3. Опpеделенность — т.е. каждое пpавило алгоpитма должно быть четким, 
однозначным и не оставлять места для пpоизвола. Благодаpя этому свойству 
выполнение алгоpитма носит механический хаpактеp и не тpебует никаких 
дополнительных указаний или сведений о pешаемой задаче. 4. Pезультативность (или конечность). Это свойство состоит в том, что алгоpитм 
должен пpиводить к pешению задачи за конечное число шагов.
5. Массовость. Это означает, что алгоpитм pешения задачи pазpабатывается в общем 
виде, т.е. он должен быть пpименим для некотоpого класса задач, pазличающихся 
лишь исходными данными. Пpи этом исходные данные могут выбиpаться из 
некотоpой области, котоpая называется областью пpименимости алгоpитма.
Формы представления алгоритмов.
    На практике наиболее распространены следующие формы представления алгоритмов:
 словесная (записи на естественном языке);

графическая (изображения из графических символов);
 псевдокоды (полуформализованные описания алгоритмов на условном 
алгоритмическом языке, включающие в себя как элементы языка программирования, 
так и фразы естественного языка, общепринятые математические обозначения и др.);
 программная (тексты на языках программирования).
    Словесный способ записи алгоритмов представляет собой описание последовательных 
этапов обработки данных. Алгоритм задается в произвольном изложении на естественном 
языке. Например. Записать алгоритм нахождения наибольшего общего делителя (НОД) 
двух натуральных чисел.
 
    Алгоритм может быть следующим:

задать два числа;
 если числа равны, то взять любое из них в качестве ответа и остановиться, в 
противном случае продолжить выполнение алгоритма;
 определить большее из чисел;

заменить большее из чисел разностью большего и меньшего из чисел;
 повторить алгоритм с шага 2. Описанный алгоритм применим к любым натуральным числам и должен приводить к 
решению поставленной задачи.
    Словесный способ не имеет широкого распространения по следующим причинам:
 такие описания строго не формализуемы;
 страдают многословностью записей;
 допускают неоднозначность толкования отдельных предписаний.
 
    Графический способ представления алгоритмов является более компактным и 
наглядным по сравнению со словесным.
    Такое графическое представление называется схемой алгоритма илиблок­схемой.
    При графическом представлении алгоритм изображается в виде последовательности 
связанных между собой функциональных блоков, каждый из которых соответствует 
выполнению одного или нескольких действий.
    В блок­схеме каждому типу действий (вводу исходных данных, вычислению значений 
выражений, проверке условий, управлению повторением действий, окончанию обработки и 
т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. 
Блочные символы соединяются линиями переходов, определяющими очередность 
выполнения действий.
В таблице приведены наиболее часто употребляемые символы.
 
Название символа
Обозначение и пример 
заполнения 
 Пояснение
 Процесс
 Решение
 
 
 Вычислительное действие или 
последовательность действий
 Проверка условий Модификация
 Предопределенный 
процесс
 Ввод­вывод
 Пуск­останов
 
 
 
 
 
 Начало цикла
 Вычисления по подпрограмме, 
стандартной подпрограмме
 Ввод­вывод в общем виде
 Начало, конец алгоритма, вход и 
выход в подпрограмму
 Документ
 Вывод результатов на печать
     Блок «процесс» применяется для обозначения действия или последовательности 
действий, изменяющих значение, форму представления или размещения данных. Для 
улучшения наглядности схемы несколько отдельных блоков обработки можно объединять 
в один блок. Представление отдельных операций достаточно свободно.
    Блок «решение» используется для обозначения переходов управления по условию. В 
каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. (Слово 
модификация означает видоизменение, преобразование). Внутри блока записывается 
параметр цикла, для которого указываются его начальное значение, граничное условие и 
шаг изменения значения параметра для каждого повторения.
    Блок «предопределенный процесс» используется для указания обращений к 
вспомогательным алгоритмам, существующим автономно в виде некоторых 
самостоятельных модулей, и для обращений к библиотечным подпрограммам. Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая, 
биологическая или биотехническая) система, способная выполнить действия, 
предписываемые алгоритмом.
    Исполнителя хаpактеpизуют:
 сpеда;
 элементаpные действия;
 cистема команд;
 отказы.
    Сpеда (или обстановка) — это «место обитания» исполнителя. Напpимеp, для 
исполнителя Pобота из школьного учебника сpеда — это бесконечное клеточное поле. 
Стены и закpашенные клетки тоже часть сpеды. А их pасположение и положение самого
Pобота задают конкpетное состояние среды.
    Система команд. Каждый исполнитель может выполнять команды только из 
некотоpого стpого заданного списка — системы команд исполнителя. Для каждой 
команды должны быть заданы условия пpименимости (в каких состояниях сpеды может
быть выполнена команда) и описаны pезультаты выполнения команды. Напpимеp, 
команда Pобота «ввеpх» может быть выполнена, если выше Pобота нет стены. Ее 
pезультат — смещение Pобота на одну клетку ввеpх.
    После вызова команды исполнитель совеpшает соответствующее элементаpное 
действие.
    Отказы исполнителя возникают, если команда вызывается пpи недопустимом для нее
состоянии сpеды.
   Обычно исполнитель ничего не знает о цели алгоpитма. Он выполняет все полученные
команды, не задавая вопросов «почему» и «зачем».
    В информатике универсальным исполнителем алгоритмов является компьютер.
    Главная особенность любого алгоритма ­ формальное исполнение, позволяющее 
выполнять заданные действия (команды) не только человеку, но и техническим 
устройствам (исполнителям). Таким образом,исполнителями алгоритмов могут быть, 
например, человек, компьютер, принтер, робот­манипулятор, станок с числовым 
программным управлением, живая клетка, дрессированное животное, 
компьютерная программа, компьютерный вирус, «черепашка» в Логомирах (геометрический исполнитель) и т.д.
    Исполнитель алгоритма — это устройство управления, соединенное с набором 
инструментов. Устройство управления понимает алгоритмы и организует их 
выполнение, командуя соответствующими инструментами. А инструменты производят 
действия, выполняя команды управляющего устройства. Прежде чем составлять 
алгоритм решения задачи, надо узнать, какие действия предполагаемый исполнитель 
может выполнить.
   Эти действия называются допустимыми действиями исполнителя. Только их и можно 
использовать.
    Исполнитель вычислительных алгоритмов называетсявычислителем. 
Вычислитель может иметь дело с числами и переменными, обозначающими числа. 
Таким образом, алгоритм — это организованная последовательность действий, 
допустимых для некоторого исполнителя. Один и тот же исполнитель может быть 
сымитирован на ЭВМ многими способами.
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных 
базовых (т.е. основных) элементов. Естественно, что при таком подходе к алгоритмам 
изучение основных принципов их конструирования должно начинаться с изучения этих 
базовых элементов. Для их описания будем использовать язык схем алгоритмов и 
школьный алгоритмический язык.
    Логическая структура любого алгоритма может быть представлена комбинацией 
трех базовых структур:
следование;
ветвление;
цикл.
 
    Характерной особенностью базовых структур является наличие в них одного входа и 
одного выхода. 1. Базовая структура следование. Образуется из последовательности действий, 
следующих одно за другим:
Алгоритмический язык
действие 1
действие 2
. . . . . . . . .
действие n
Язык блок­схем  
 
    2. Базовая структура ветвление. Обеспечивает в зависимости от результата проверки 
условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый
из путей ведет к общему выходу, так что работа алгоритма будет продолжаться 
независимо от того, какой путь будет выбран.
Структура ветвление существует в четырех основных вариантах:
если­то;
если­то­иначе;
выбор;
выбор­иначе. Алгоритмический язык  Язык блок­схем
если условие
то действия
все
 
 если условие
то действия 1
иначе действия 2
все
 
 
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
все
 
 
 выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
иначе действия N+1 все
 
 
Примеры команды если
если x > 0
то y := sin(x)
все
 
 если a > b
то a := 2*a; b := 1
иначе b := 2*b
все
 
 выбор
при n = 1: y := sin(x)
при n = 2: y := cos(x)
при n = 3: y := 0
все
 
 выбор
при a > 5: i := i+1
при a = 0: j := j+1
иначе i := 10; j:=0
все
 
     3. Базовая структура цикл. Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла. Основные разновидности 
циклов представлены в таблице:
Алгоритмический язык Язык блок­схем 
Цикл типа пока
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное
после слова пока.
 нц пока условие
тело цикла (последовательность действий)
кц
 
Цикл типа для
Предписывает выполнять тело цикла для всех значений некоторой переменной 
(параметра цикла) в заданном диапазоне.
 нц для i от i1 до i2
тело цикла (последовательность действий)
кц
 
 
Примеры команд пока и для
 нц пока i <= 5
S := S+A[i] i := i+1
 
кц
 
нц для i от 1 до 5
X[i] := i*i*i
Y[i] := X[i]/2
кц