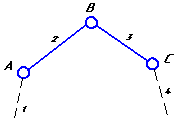
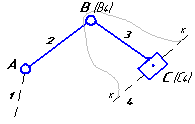
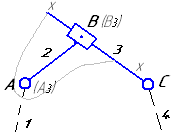
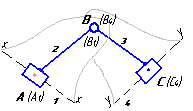
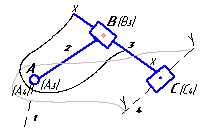
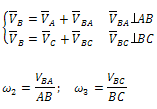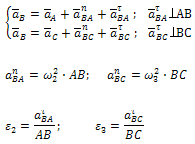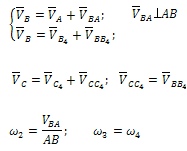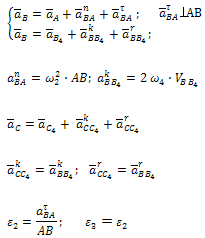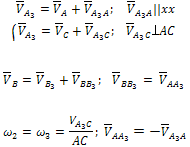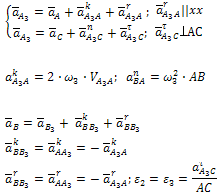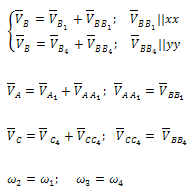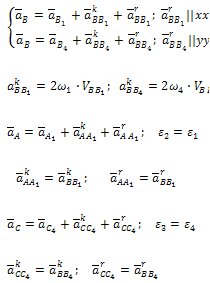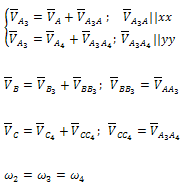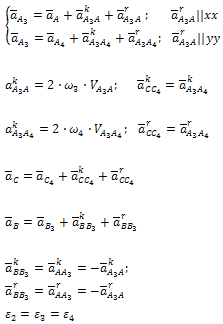Рассмотрим порядок построения планов скоростей и ускорений точек звеньев на примере кинематического исследования плоского рычажного механизма (рисунок 1).
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:
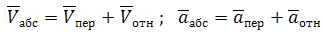
На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.
На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.
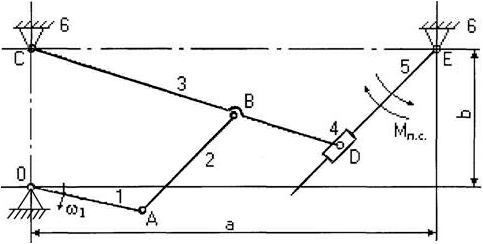
Рисунок 1 – Кинематическая схема плоского рычажного механизма
Другие примеры решений >
Помощь с решением задач >
Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.
Начальный механизм:
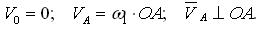
Здесь
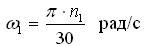
По вычисленному значению VA выбираем масштаб плана скоростей KV и из произвольного полюса откладываем отрезок va изображающий эту скорость:
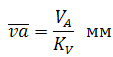
Можно также назначать отрезок va а масштаб KV вычислять:
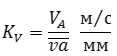
Группа Ассура второго класса 1-го вида (звенья 2, 3):
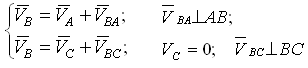
Истинные значения (в м/с) относительных скоростей VBA и VBC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:
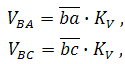
а зная их, можно определить и угловые скорости звеньев 2 и 3:
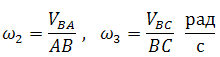
Скорость точки D на плане скоростей можно определить по подобию. (Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:
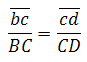
Группа Ассура второго класса 3-го вида (звенья 4,5) :
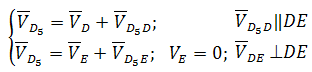
где D5 — точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D5 относительно точки E можно вычислить угловую скорость звеньев 4 и 5 (ω4=ω5, т. к. эти звенья соединяются поступательной парой):
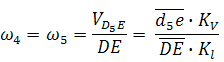
Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.
План ускорений строится в таком же порядке.
Начальный механизм
Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена (ω1=соnst):
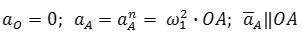
По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):
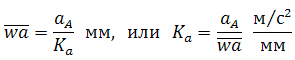
Здесь точка w – полюс плана ускорений.
Группа Ассура (звенья 2,3) второго класса 1-го вида:
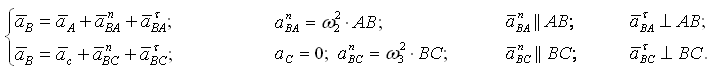
После построения определяются aτBA и aτBC, по которым можно вычислить угловые ускорения звеньев 2 и 3:
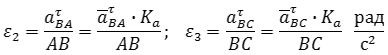
Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:
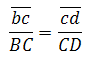
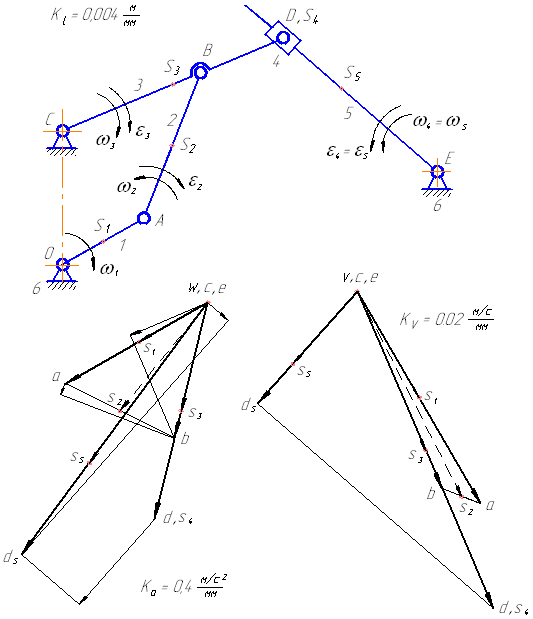
Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма
Группа Ассура (звенья 4,5) второго класса 3-го вида:
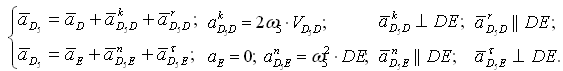
Для определения направления akD5D надо вектор VD5D повернуть на 90° в направлении ω5. Угловые ускорения:
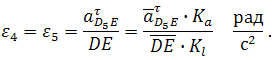
При силовом расчете необходимо иметь ускорения центров масс (asi), которые на плане ускорений определяются методом подобия.
Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.
Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.
Таблица 1 – Кинематический анализ групп Ассура II класса методом планов
| Вид группы |
Конфигурация |
Уравнения для построения планов скоростей и для определения угловых скоростей | Уравнения для построения планов ускорений и для определения угловых ускорений |
|
1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
Пример расчета механизма с поступательно движущимся выходным звеном >
Курсовой проект по ТММ >
Сначала
строится план механизма в выбранном
масштабе длин ML
и в той позиции, в которой сила полезных
сопротивлений РПС,
приложенная к ползуну 5, максимальна.
Это желательно сделать по следующим
причинам: знание величин ускорений
звеньев необходимо для расчета сил
инерции и моментов сил инерции, а при
проведении силового анализа механизма
целесообразно рассматривать именно то
положение механизма, которое нагружено
максимальной силой РПС.
Для того чтобы его определить, необходимо
на прямой HD
хода ползуна (смотри совмещенные планы
механизма) построить график изменения
силы PПС
и определить искомую позицию механизма.
Ускорение
точки А кривошипа определяется с
использованием векторного уравнения
ускорения точки А кривошипа относительно
оси вращения О:
аА
=
аАО
=
аnАО
+
аАО,
где
а
nАО
–
нормальная составляющая ускорения
точки А относительно О;
а
АО
—
тангенциальная составляющая ускорения
А относительно О.
Так
как по условий задачи угловая скорость
кривошипа постоянна (W1
=
const),
то угловое ускорение 1
=
0 , а тангенциальная составляющая
ускорения также равна нулю:
аАО
= 1
.
LOA
=
0.
Тогда
полное ускорение точки А равно нормальной
составляющей ускорения: аА
=
аnАО,
причем
аnАО
=
21
.
LOA,
м/с2.
Вектор
ускорения аnАО
параллелен ОА и направлен от А к 0.
Затем
определяется ускорение точки С2
, принадлежащей кулисе 2.
Для
этого составляются следующие векторные
уравнения ускорений:
а)
для звена 2 (кулисы)
aC2
=
аА
+
anC2А
+
aC2A
;
б)
для звена 3 (качающегося камня):
aC2
=
aC3
+
akC2C3
+
aОТНC2C3.
Рассчитываются
величины ускорений, входящих в эти
векторные уравнения:
нормальное
anC2А
=
V2C2A/LAC2
,
м/с2;
Кориолисово
akC2С3
=
2 VC2C3
.
2,
м/c2.
Причемвектор
нормального ускорения anC2А
параллелен АС2
и направлен от С2
к A.
Для
определения направления вектора
Кориолисова ускорения akC2C3
нужно вектор С2С3
относительной скорости VC2C3
повернуть на 90° по направлению угловой
скорости 2
кулисы.
Вектор тангенциальной составляющей
ускорения aC2A
перпендикулярен АС2,
а вектор относительного (релятивного)
ускорения aОТНC2C3
параллелен АС2.
Причем здесь имеется в виду, что нормальное
ускорение a
nC2С3
=
0, если звено АС2
– прямая линия.
Неизвестные
величины aC2A
и
aОТНC2C3
находятся построением плана ускорений
(рис.7). Для этого сначала выбирается
масштаб плана ускорений:
Ма
=
aА/(Раа΄),
м/с2/мм,
где
(Раа΄)
— длина вектора в мм, изображающего
ускорение аА
на плане ускорений.
Величина
(Раа΄)
выбирается произвольно из расчета,
чтобы масштаб был удобен для расчетов
(желательно круглое число), а план
ускорений разместился на отведенном
месте чертежа. Построение плана ускорений
осуществляется в соответствии с
последовательностью написания
вышеприведенных векторных уравнений.
Сначала
строится (т.е. изображается графически)
первое векторное уравнение, для чего
из произвольно выбранного полюса РА
(рис.7) параллельно отрезку ОА (см. план
механизма) проводится вектор Раа
с ранее выбранной длиной (см. расчет
масштаба Ма
). Он изображает ускорение аА
=
аnАО.
Из точки a΄
параллельно АС2
проводится
вектор (а΄n2)
, изображающий вектор anC2A.
Длина вектора (a΄n2)
вычисляется по формуле:
a‘n2
=
anC2A/Ма,
мм.
Через
точку n2
проводится луч по направлению ускорения
aC2A
перпендикулярно АС2.
Затем
строится второе векторное уравнение.
Из полюса Ра
проводится вектор (Раk)
длиной Раk
= akC2C3/Ма,
мм, изoбражающий Кориолисово ускорение
akC2C3.
Из точки К проводится луч по направлению
ускорения aОТНC2C3,
параллельный
АС2.
В
месте пересечения лучей получается
точка С2‘,
которую соединяют c полюсом Ра
и точкой а΄.
Вектор n2c2΄
изображает ускорение aC2A
, вектор (kC2΄)
– ускорение aОТНC2C3,а
вектор(a‘c‘2)
– полное ускорение aC2A.
Для
определения ускорения точки В используется
теорема
подобия:
отрезки
относительных ускорений на плане
ускорений образуют фигуру, подобную
соответствующей фигуре на плане
механизма.
В
соответствии с ней составляется уравнение
пропорции отрезков на плане механизма
и плане ускорений:
(а’2c’2/АС2)
= ( а’b’/AB),
откуда
вычисляют длину отрезка
(а’b’)
= (а2‘c2‘
.
АВ)/АС2
, мм
и
откладывают этот отрезок от точки а’ в
сторону точки с’2
на плане ускорений. Соединив полюс Ра
с точкой b’,
получают полное ускорение точки В aB,
причем
aB
=
(Ра
b’)
.
Ма,
м/с2.
Определяют
ускорение точки Д. Для этого составляется
векторное уравнение ускорений шатуна
4
аD
=
aB
+
anDB
+
aDB.
Вычисляется
величина нормального ускорения:
anDB
=
V2DB/LBD,
м/с2.
Из
точки b΄
параллельно звену ВД откладывается
вектор (b΄n4)
длиной b΄n4
=
anDB/МА
, мм , изображающий на плане ускорение
anDB.
Через точку n4
проводится луч, перпендикулярный ДВ,
до пересечения с проведенной из полюса
Ра
прямой, параллельной движению ползуна
5. В месте пересечения получается точка
d’.
Вектор (Раd‘)
изображает полное ускорение точки Д –
ad,
а вектор (n4b’)
— тангенциальное ускорение aDB.
Вычисляется величина этого ускорения
aDB
=
(n4d΄).
Вычисляются
величины угловых ускорений звеньев 2
(кулисы) и 4 (шатуна):
2
=
aC2A/LAC2,1/с2
;
4
=
aDB/LBD,
1/с2.
Направления
угловых ускорений определяются по тому,
куда «вращают» векторы aC2A
и aDB
звенья 2 и 4 , если их перенести соответственно
в точки С2
и Д плана механизма.
Для
определения радиуса кривизны траектории
движения точки В, совершающей сложное
движение, используется формула
=
V2B/anB
, м
,
где
VB=(РVb)
.
MV,
м/с — скорость точки В.
Для
ее нахождения необходимо полное ускорение
точки В разложить на нормальную и
тангенциальную составляющие:
aВ
=
anB
+
aB
.
Это
можно сделать графически на построенном
плане ускорений, причем нормальная
составляющая ускорения точки В anB
будет направлена перпендикулярно
скорости VB
, а тангенциальная – aB
–
параллельно скорости VB
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кинематическая схема механизма предназначена для определения
положений, траекторий, скоростей и ускорений точек и звеньев механизма. Для
построения кинематических схем используются условные обозначения согласно ГОСТ
2770 – 68.
Планы положений механизма строятся методом засечек в
масштабе (рис.2). В отличие от масштабов, применяемых в машиностроении, в
теории механизмов и машин масштабы представляют собой именованные числа.
Масштабы обозначаются буквой К с соответствующим индексом:
Масштабы длин и пути 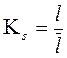 ,
,
м /мм;
Масштаб скоростей 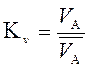 , м/с.мм;
, м/с.мм;
Масштаб ускорений ![]()
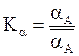 , м/с2.мм.
, м/с2.мм.![]()
Численное значение масштаба должно быть либо десятичной
дробью, либо целым числом и включать в себя стандартные цифры или комбинации
цифр: 1, 2, 4, 5, 15, 25, 75, 10, 20…….
Для выполнения кинематического анализа данного механизма в
задаче № 1 требуется вычертить в выбранном масштабе Кs
положение механизма изображенное в задании и для него построить план скоростей
и ускорений ![]()
1.2.2. Построение планов скоростей и ускорений
Метод построения планов скоростей и ускорений основан на
теореме о разложении движения, согласно которой любое движение можно
представить как сумму двух простых движений – переносного /поступательного/ и
относительного /вращательного/. Тогда для скоростей:
![]()
для ускорений:
![]() ,
,
где ![]() — нормальная составляющая ускорения
— нормальная составляющая ускорения
в относительном движении /определяется по данным плана скоростей/, на плане
ускорений всегда направлена вдоль звена к центру относительного движения;
![]() — касательная составляющая
— касательная составляющая
/определяется графически/ на плане ускорений, всегда направлена перпендикулярно
к звену /радиусу/ относительного движения.
Для определения скорости или ускорения
точки графическим путем не-обходимо составить систему из двух векторных
уравнений. При составлении векторных уравнений движение точки рассматривается
относительно двух других точек, с которыми эта точка связана и скорости которых
уже известны.
Пример:
Построить план скоростей и план
ускорений для заданного положения механизма, изображенного на рисунке 2.
Пусть заданы размеры звеньев
механизма: ОА = 150мм; АВ = 450мм и т.д. и частота вращения входного звена /
кривошипа/ОА/, соответствующая n = 200 об/мин.
План скоростей рис.3.
Скорость пальца кривошипа /точка А/
определяется по формуле:
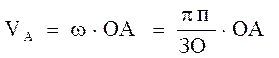 ,
,
где n — частота вращения кривошипа, об/мин;
ОА – длина
кривошипа, м;
Подставляя данные в формулу,
получим:
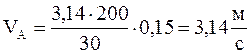
Задаваясь длиной отрезка ![]() /мм/, изображающего на плане скоростей
/мм/, изображающего на плане скоростей
вектор скорости точки А, получим масштаб плана ![]() :
:
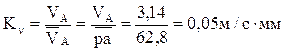
Отрезок ![]() :
:
![]() = 62,8 мм
= 62,8 мм
выбран так, чтобы
был получен стандартный масштаб скоростей.
Рекомендуется выбирать отрезок ![]() не менее 50мм.
не менее 50мм.
Из полюса плата скоростей р отложим
вектор скорости точки А ![]() перпендикулярно
перпендикулярно
звену ОА/ по касательной к траектории движения точки А/ в сторону ее движения.
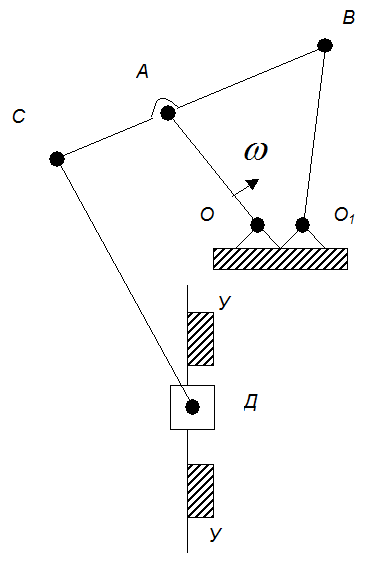
Рис.2. План механизма
КS=………………м/мм
.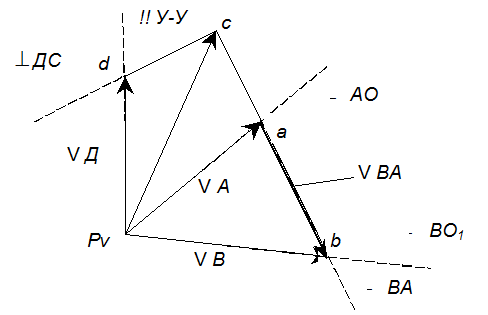
Рис.3. План скоростей
КV…………………….м/с*мм
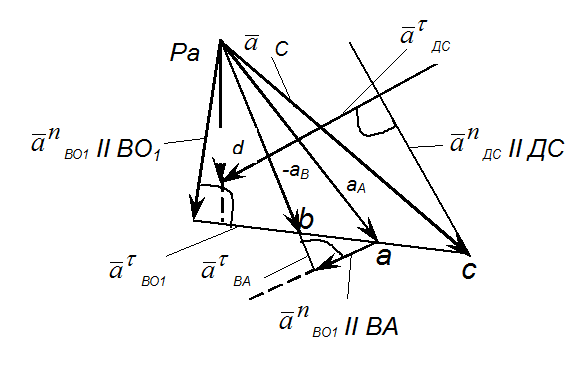 Рис.4. План ускорений
Рис.4. План ускорений
Кa……………………………м/с2мм
Рассматривая движение точки В относительно точки А, а затем
относительно ОI, имеем:
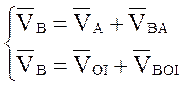
Из конца вектора скорости ![]() /точка
/точка
а/ проводим линию действия вектора относительной скорости ![]() перпендикулярно звену АВ, а затем из
перпендикулярно звену АВ, а затем из
полюса p /т.к. V0 =
0/ перпендикулярно звену ВОI проводим
линию действия вектора относительной скорости ![]() до
до
пересечения с линией действия вектора ![]() в
в
точке в. Отрезок![]() изображает вектор
изображает вектор
абсолютной скорости точки В ![]() .
.
Скорость точки С /третьей точки звена ВАС/ найдем методом
подобия. Можно записать следующее соотношение:
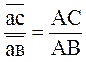 или
или 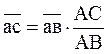 ,
,
где ![]() и
и ![]() — отрезки на плане скоростей;
— отрезки на плане скоростей;
АС и АВ – размеры звеньев
механизма.
Вычислив отрезок ![]() и отложив его на
и отложив его на
плане скоростей, получим точку ![]() . Соединяя точку
. Соединяя точку ![]() с полюсом
с полюсом ![]() , найдем отрезок
, найдем отрезок ![]() , изображающий вектор абсолютной
, изображающий вектор абсолютной
скорости точки С (Vc).
Для определения скорости точки Д рассмотрим движение этой
точки относительно точек С и Ду / точка Ду принадлежит
неподвижным направляющим и в данный момент совпадает с точкой Д /.
Система векторных уравнений имеет вид:
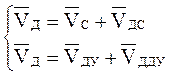
Так как VДУ =0, то ![]() .
.
Из конца вектора скорости ![]() точка
точка
с / проводим линию действия вектора относительной скорости ![]() перпендикулярно звену СД,
перпендикулярно звену СД,
а из полюса p параллельно оси у-у проводим линию
действия вектора относительной скорости ![]() в
в
точке d . Отрезок ![]() изображает вектор абсолютной
изображает вектор абсолютной
скорости точки Д ![]() .
.
Абсолютные скорости каждой точки равны:
VВ = ![]() , м/с
, м/с
VС = ![]() , м/с
, м/с
VД = ![]() , м/с
, м/с
Относительные скорости:
VВА = ![]()
![]() =
= ![]()
VДС = ![]()
План ускорений рис.4.
Рассматривая движение точки А относительно точки О, можно
записать:
![]()
Ускорение ао = 0, 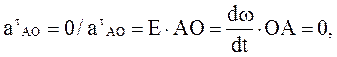 т.к.
т.к.
![]() сonst. Следовательно, точка А при
сonst. Следовательно, точка А при
постоянной угловой скорости кривошипа будет иметь только нормальное /
центральное/ ускорение:
![]()
Величина нормального ускорения: 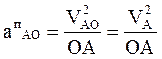
Подставляя числовые значения, получим:
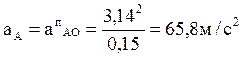
Задаваясь длиной отрезка ![]() изображаемого
изображаемого
на плане ускорений вектор ускорения точки А, получим масштаб плана ускорений ![]()
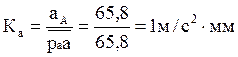
Отрезок ![]() выбран равным 65,8 мм, чтобы получить стандартный масштаб ускорений.
выбран равным 65,8 мм, чтобы получить стандартный масштаб ускорений.
Из полюса плана ускорений ![]() откладываем
откладываем
вектор ускорения точки А ![]()
/отрезок ![]() /
/
параллельно звену АО, направляя его от точки А к центру ее вращения – точке О.
Рассматривая движение точки В относительно точки А, а затем
относительно точки О1, имеем:
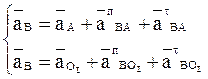
Так как ![]() то
то ![]() .
.
Нормальное ускорение В в
ее относительном движении относительно точки А по величине определяется
следующим образом:
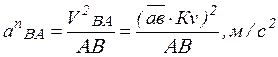
Удобнее сразу находить величину отрезка, изображаемого
вектор нормального ускорения:
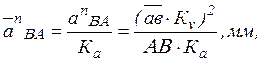
где ![]() —
—
отрезок, изображений вектор относительной скорости ![]() на
на
плане скоростей, мм;
АВ – длина шатуна, м.
Направлен вектор ![]() по шатуну от точки
по шатуну от точки
В к точке А.
Вектор касательного ускорения ![]() известен
известен
только по направлению – линия его действия перпендикулярна звену ВА.
Нормальное ускорение:
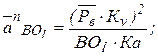
![]()
![]()