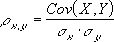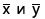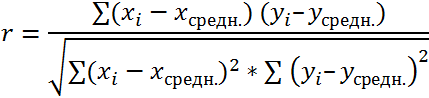Excel – это эффективный инструмент для статистической обработки данных. И определение корреляций является очень важной составляющей этого процесса. Программа имеет весь необходимый инструментарий для осуществления расчетов такого плана. Сегодня мы более детально разберемся, что нам нужно для осуществления анализа этого типа.
Содержание
- Что представляет собой корреляционный анализ
- Корреляционный анализ в Excel — 2 способа
- Как рассчитать коэффициент корреляции
- Способ 1. Определение корреляции с помощью Мастера Функций
- Способ 2. Вычисление корреляции с помощью пакета анализа
- Как построить поле корреляции в Excel
- Диаграмма рассеивания. Поле корреляции
Что представляет собой корреляционный анализ
Простыми словами, корреляция – это связь между двумя явлениями. В свою очередь, под корреляционным анализом подразумевают выявление этой связи. Очень частое утверждение гласит, что корреляция – это зависимость между разными объектами, но на деле это неточное определение. Ведь существует множество изображений, которые показывают связь между явлениями, которые никак не могут быть зависимы друг от друга или одного третьего фактора, который влияет на них.
Для определения зависимости используется другой тип анализа, который называется регрессионным.
Величина, определяющая степень выраженности взаимосвязи, называется коэффициентом корреляции. Это единственная величина, которая рассчитывается корреляционным анализом по сравнению с регрессионным. Возможные вариации коэффициента корреляции могут быть в пределах от -1 до 1. Если это число положительное, взаимосвязь между динамикой изменения значений прямая. Если же отрицательное, то увеличение числа 1 приводит к аналогичному уменьшению числа 2. Если число меньше единицы по модулю, то корреляция неполная. Например, увеличение числа 1 на единицу приводит к увеличению числа 2 на 0,5. В таком случае коэффициент корреляции составляет 0,5. Если же коэффициент корреляции составляет 0, то взаимосвязи между двумя переменными нет.
Интересный факт: корреляции делятся на истинные и ложные. То есть, иногда то, что графики идут в одинаковом направлении, может быть чистой случайностью, а не закономерным следствием воздействия одной переменной на другую или влияния общего фактора на обе переменные. В узких кругах довольно популярны картинки, где коррелируют между собой абсолютно не связанные явления. Вот некоторые примеры:
- Количество человек, которые стали утопленниками в бассейнах, четко коррелирует с количеством фильмов, в которых Николас Кейдж был актером.
- Количество съеденной моцареллы и количество человек, которые получили докторскую степень, также коррелирует на протяжении 2000-2009 годов. Наверно, действительно, моцарелла как-то влияет на мозг и стимулирует желание совершать научные открытия.
- Почти во всех случаях средний возраст женщин, которые получили статус «Мисс Америка» коррелирует с количеством людей, которые погибли от нахождения в горячем паре.
- Число людей, которое погибло в результате дорожно-транспортного происшествия, четко коррелирует с количеством сметаны, которое съедают люди.
- Мало кто знает, что чем больше курятины человек ест, тем больше сырой нефти импортируется в мире. Правда, это тоже пример ложной корреляции. Кстати, импорт сырой нефти родом из Норвегии тесно связано с количеством людей, которые погибли в результате столкновения автомобиля с поездом. Причем в этом случае корреляция почти 100 процентов.
- А еще маргарин негативно влияет на статистику разводов. Чем больше людей, которые проживали в штате Мэн, потребляли маргарина, тем выше была частота разводов. Правда, здесь еще может быть рациональное зерно. Ведь частота потребления маргарина имеет обратную корреляцию с экономическим положением в семье. В свою очередь, плохое экономическое положение в семье имеет непосредственную связь с количеством разводов. И это уже доказано научно. Так что кто знает, может, эта корреляция и не является такой ложной. Правда, никто этого не перепроверял.
- Количество денег, которое правительство США тратит на развитие науки, космоса и технологий, имеет тесную связь с количеством самоубийств, проведенных в форме повешения или удушения.
Ну и наконец, еще один пример ложной корреляции – чем больше сыра люди едят, тем больше людей умирает из-за того, что они запутываются в своих простынях.
Поэтому несмотря на то, что корреляция является эффективным статистическим инструментом, нужно учиться отфильтровывать истинные взаимосвязи между явлениями и ложные. Иначе исследование может получить такие интересные результаты. А теперь переходим непосредственно к тому, как проводить корреляционный анализ в Excel.
Корреляционный анализ в Excel — 2 способа
Вычисление коэффициента корреляции осуществляется двумя способами. Первый – это использование Мастера функций, который позволяет ввести формулу КОРРЕЛ. Второй инструмент – это пакет анализа, требующий отдельной активации.
Как рассчитать коэффициент корреляции
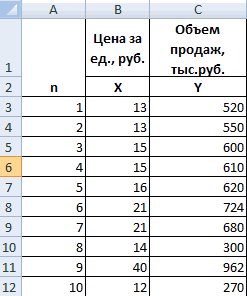
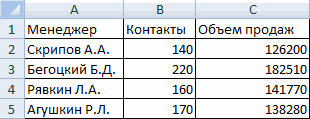
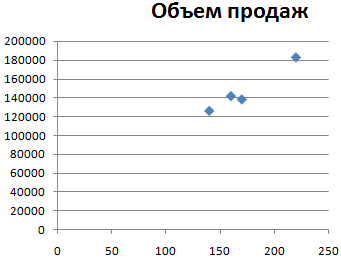
Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.
Способ 1. Определение корреляции с помощью Мастера Функций
Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:
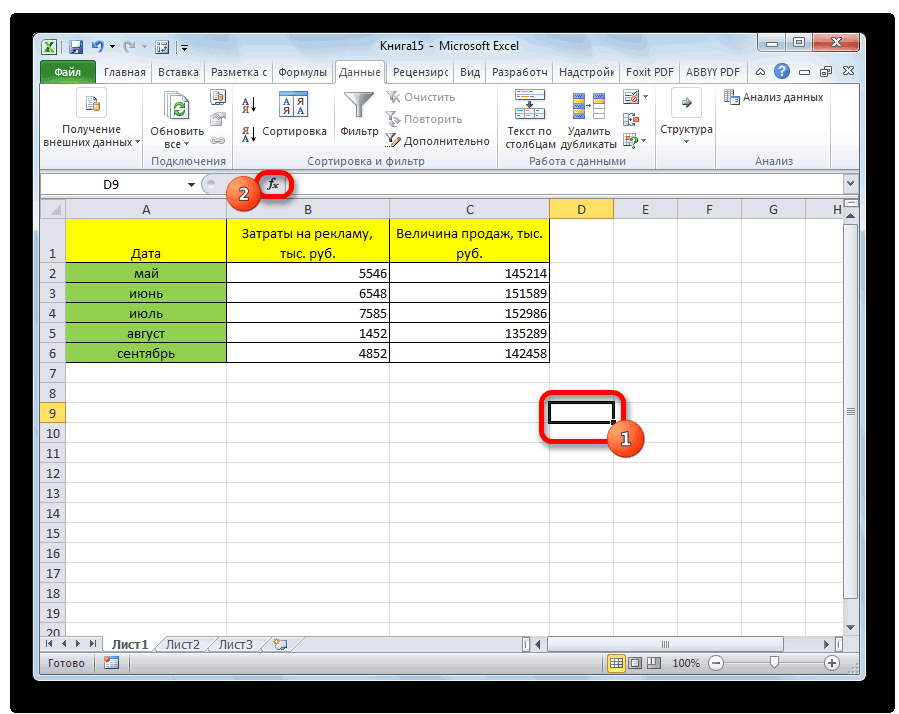
- С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций.
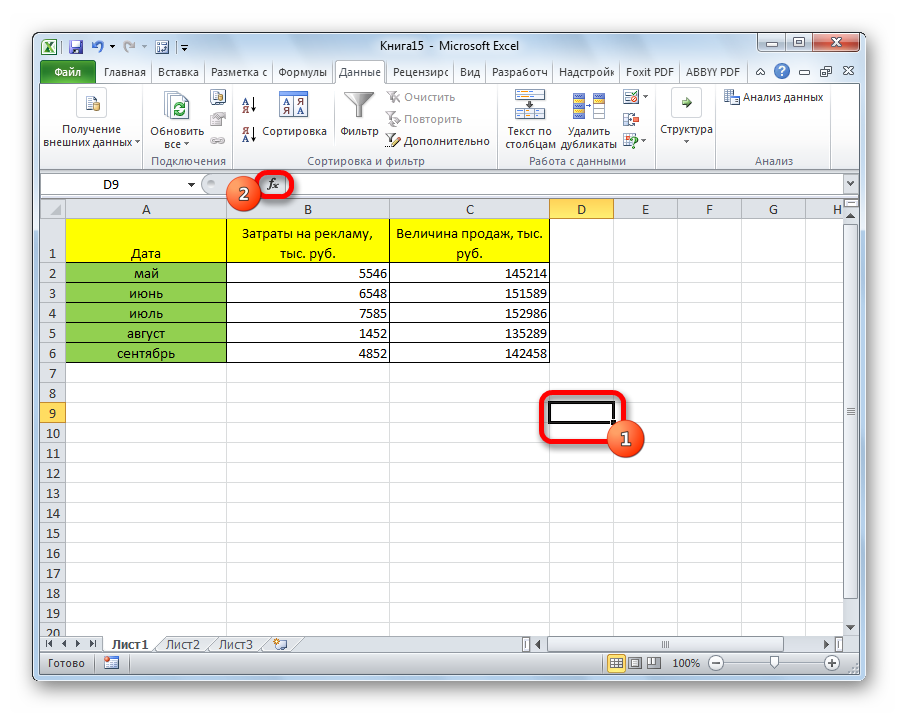
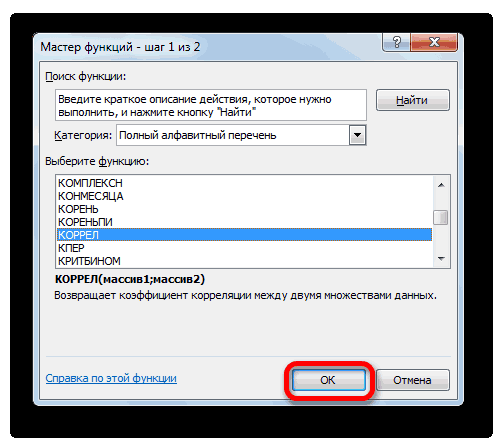
- Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке.
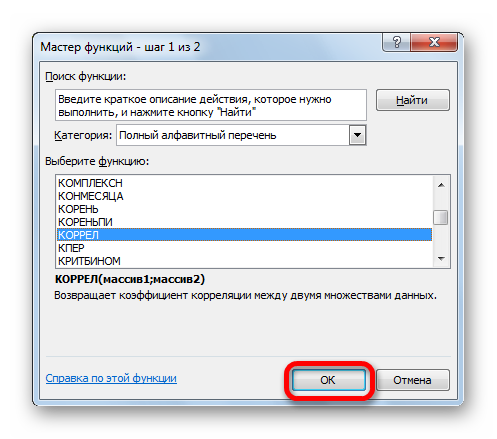
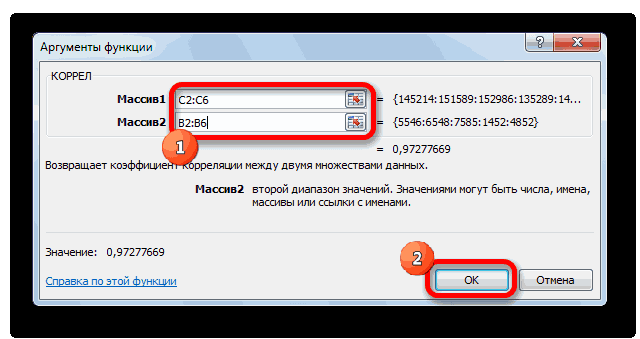
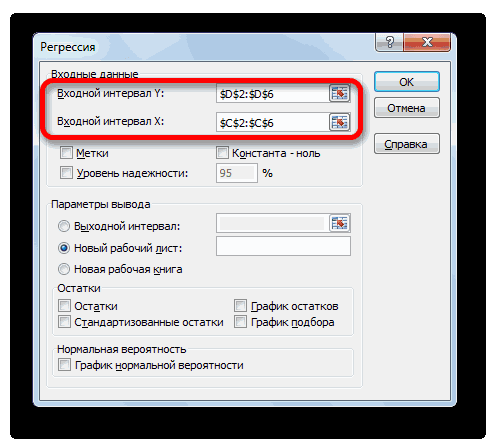
- Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон.
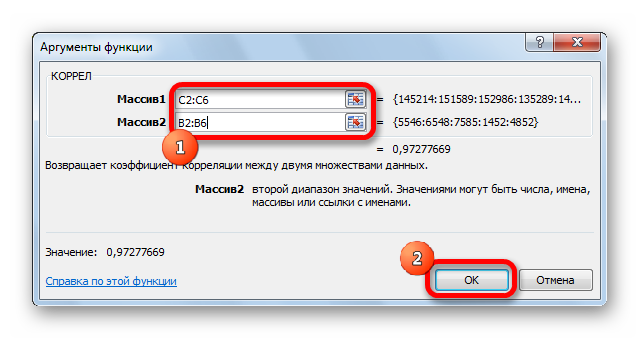
- После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.
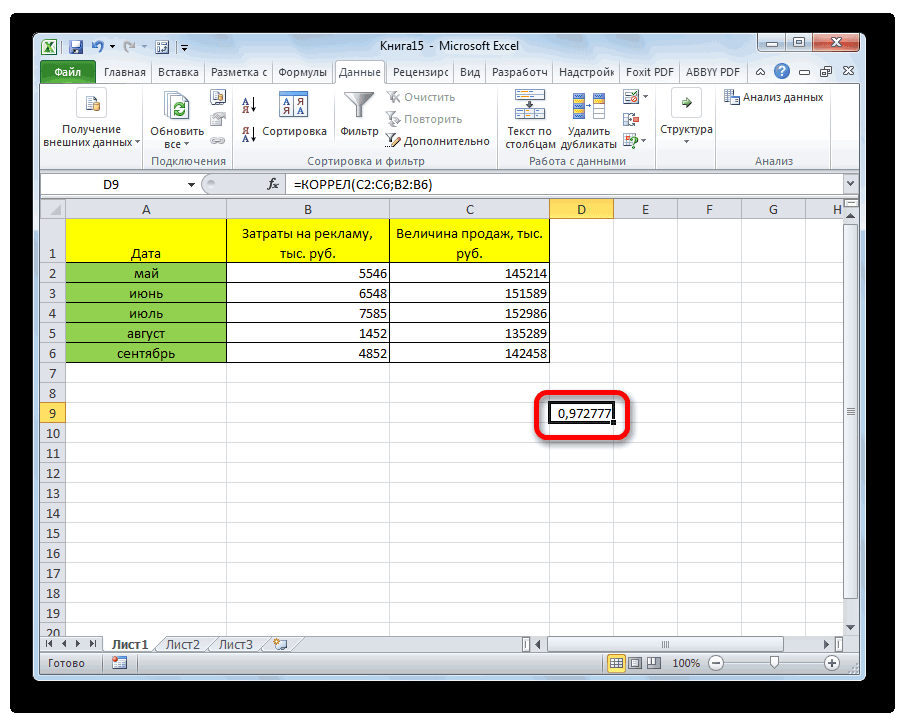
После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов.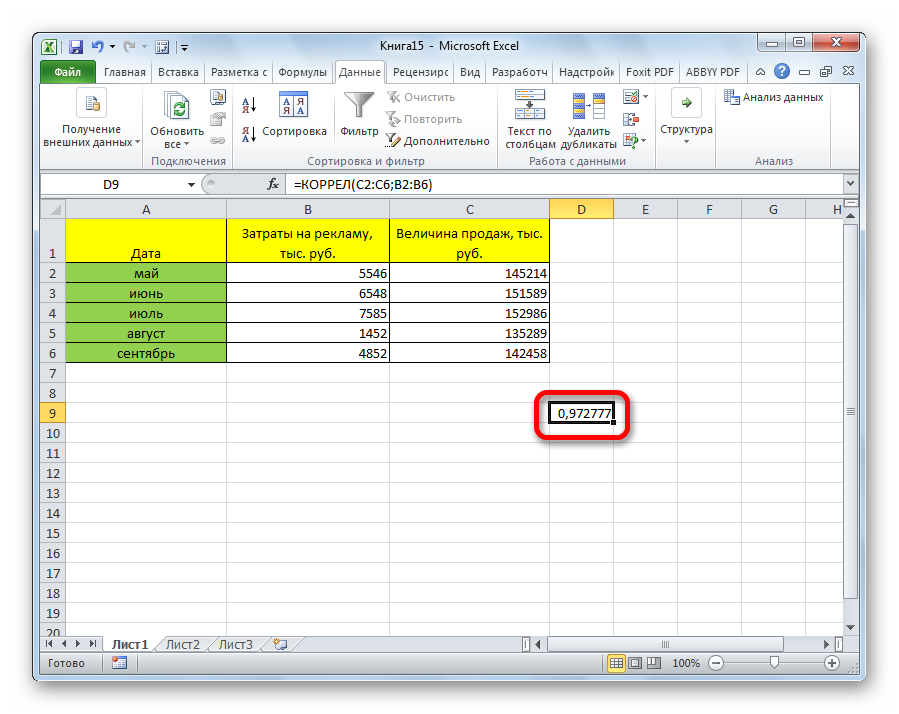 
Способ 2. Вычисление корреляции с помощью пакета анализа
Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:
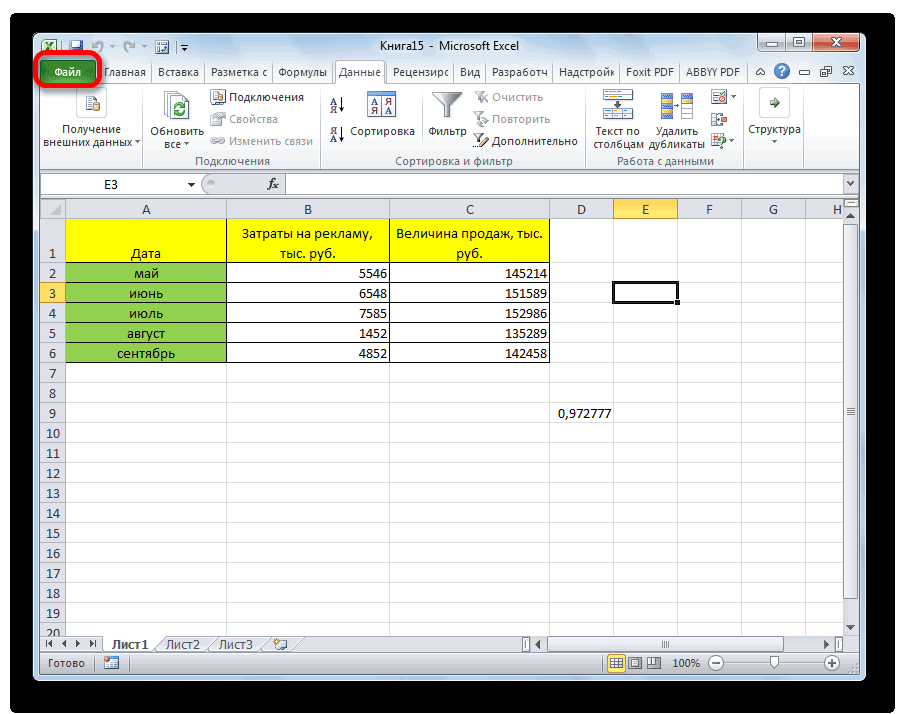
- Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная».
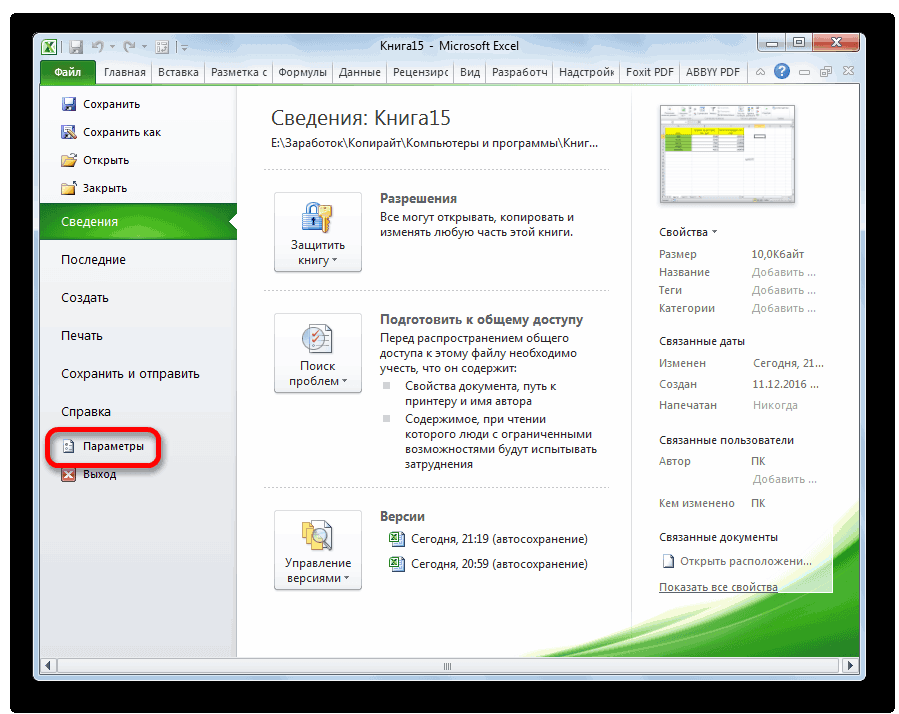
- После этого открываем раздел с настройками.
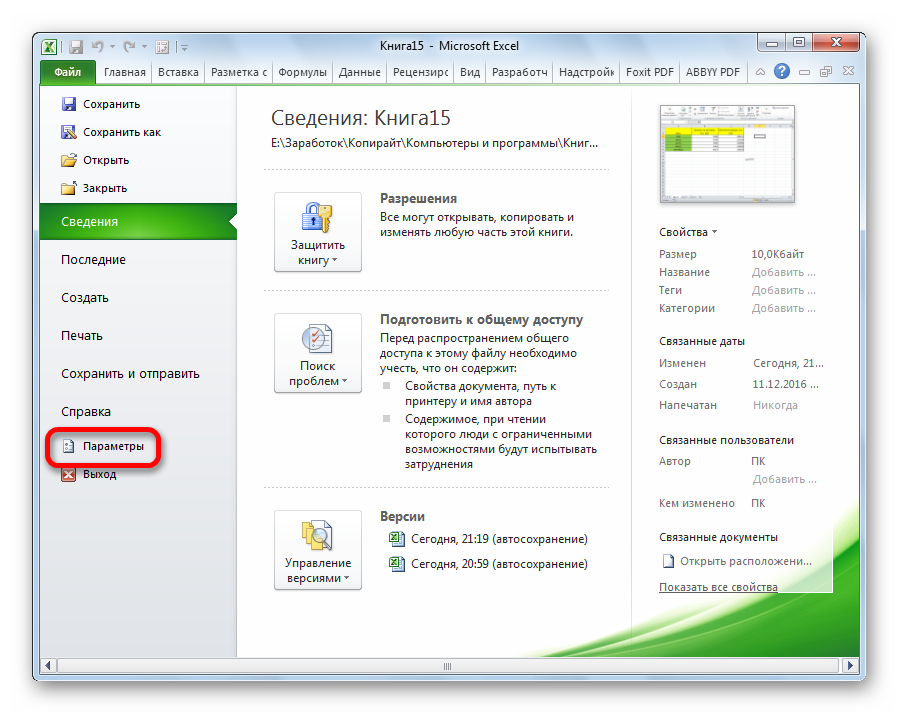
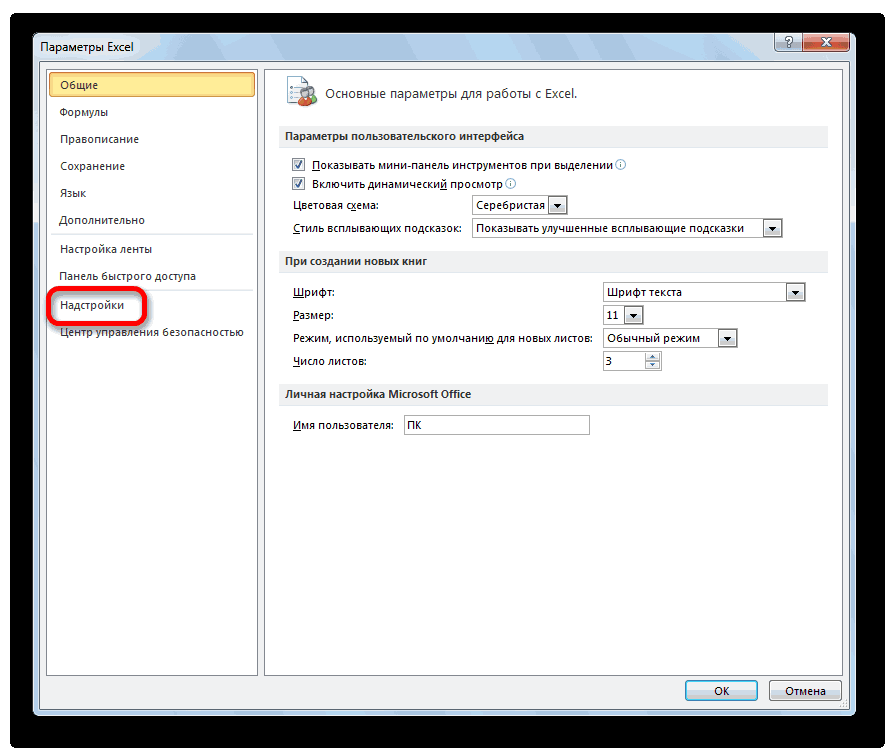
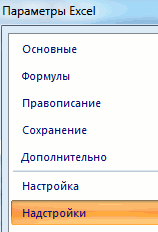
- В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи.
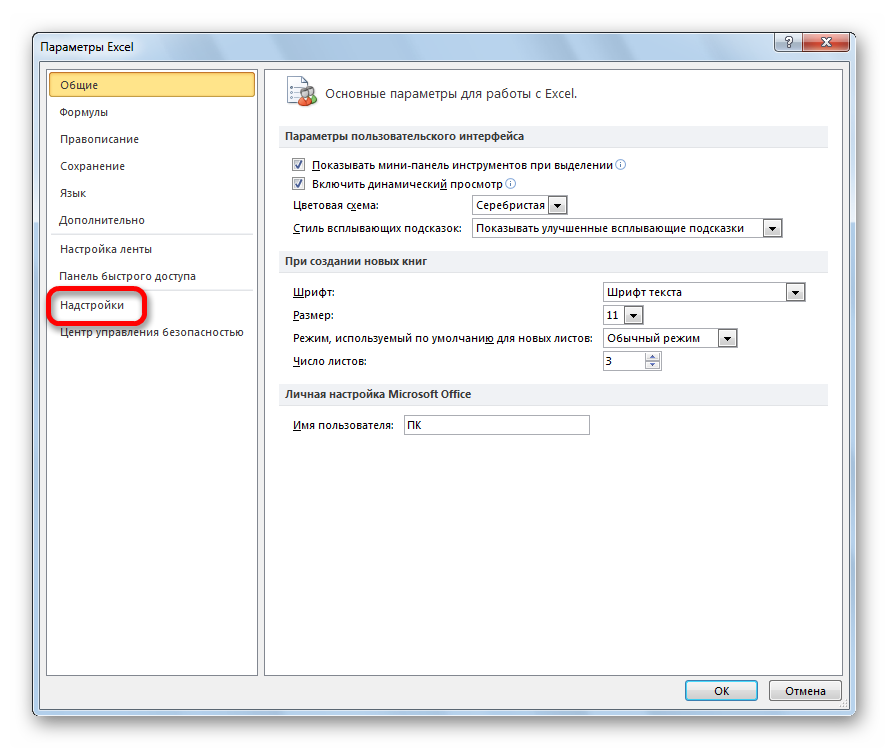
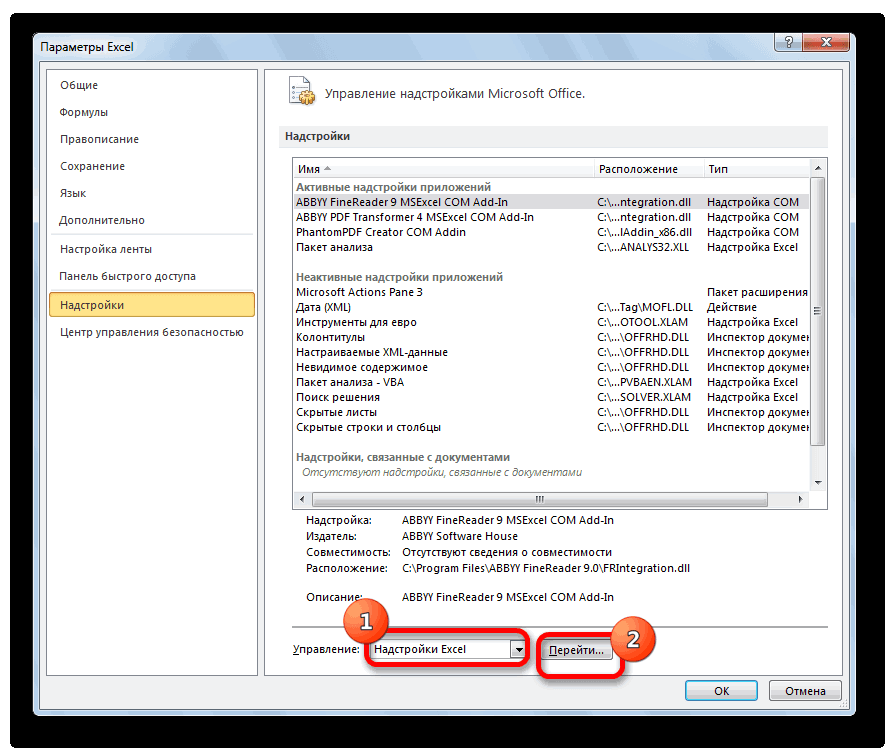
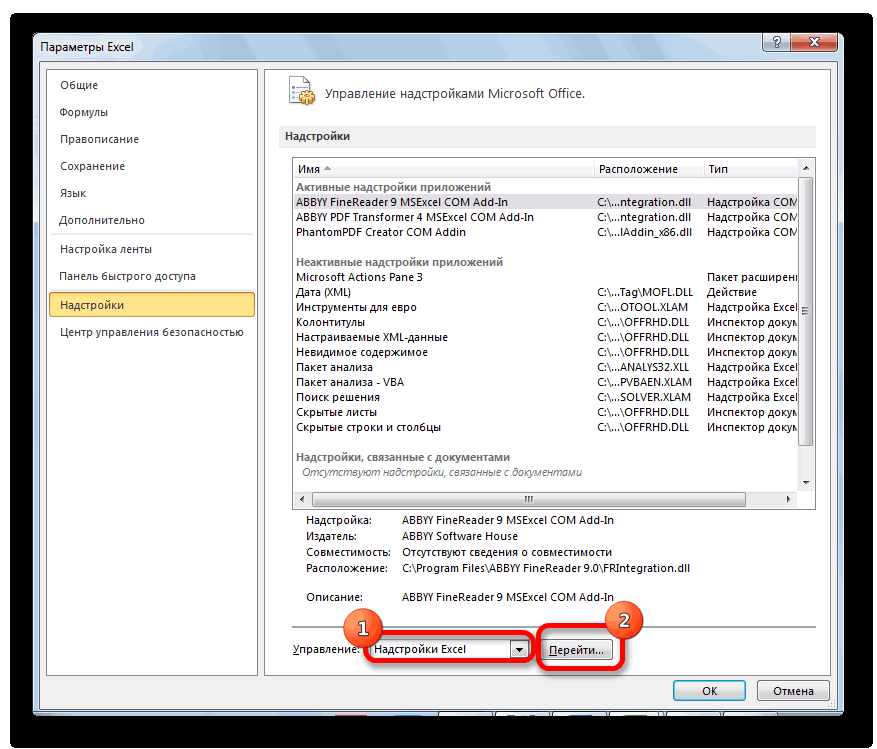
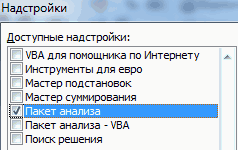
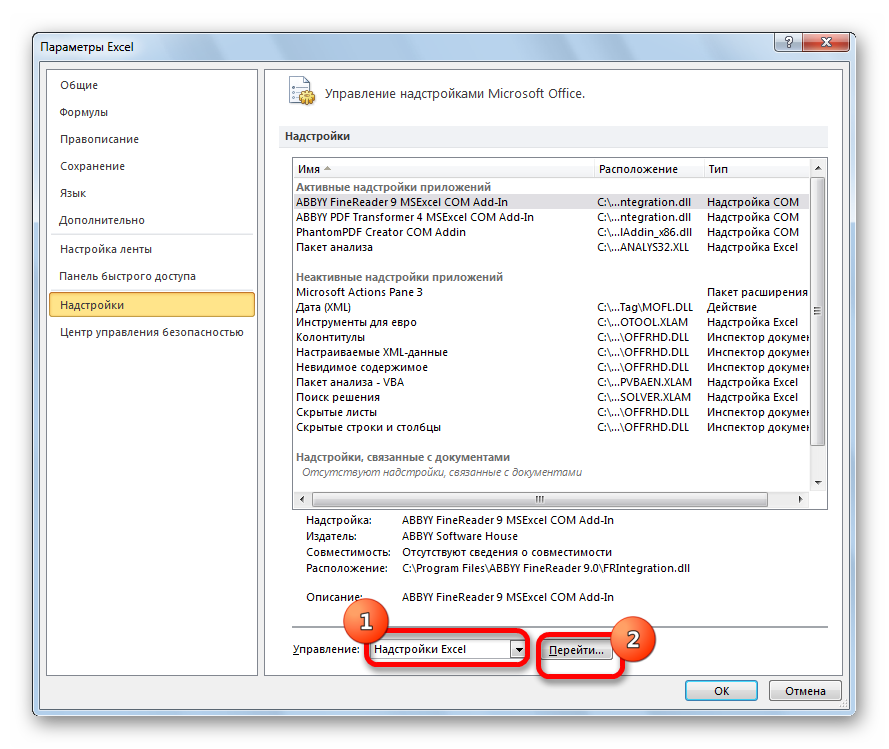
- Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений.
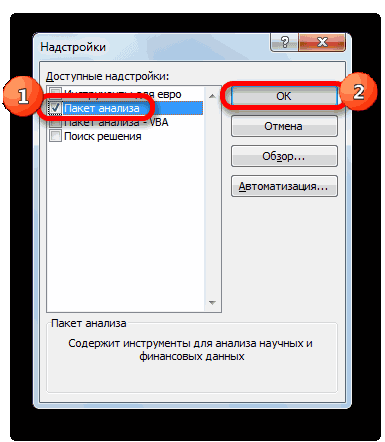
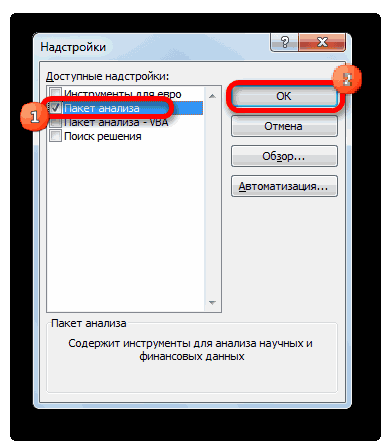
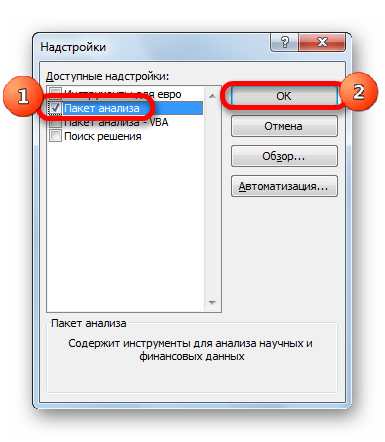
- Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК».
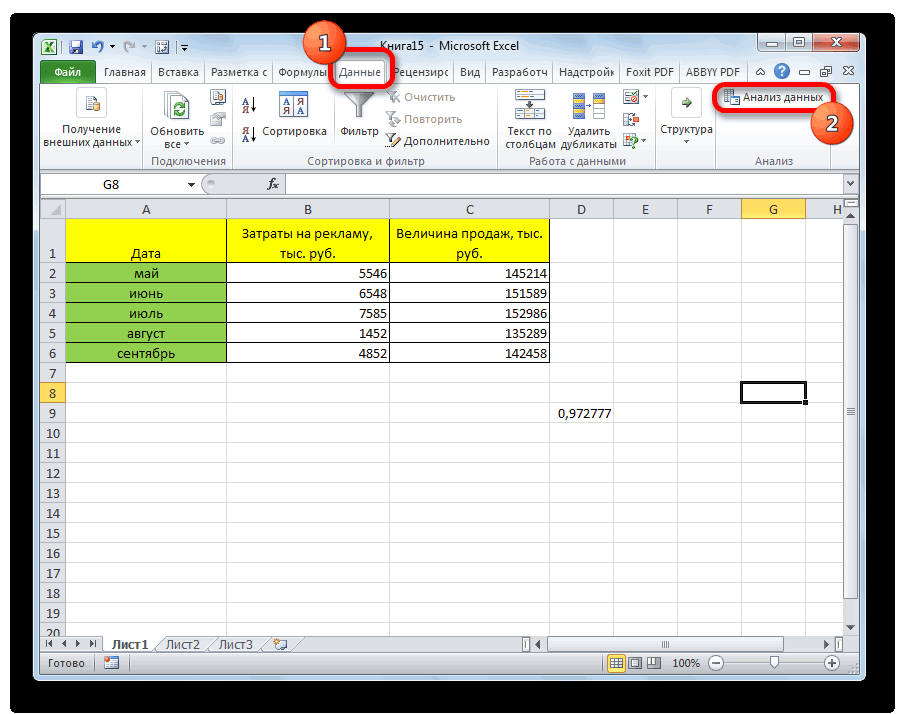
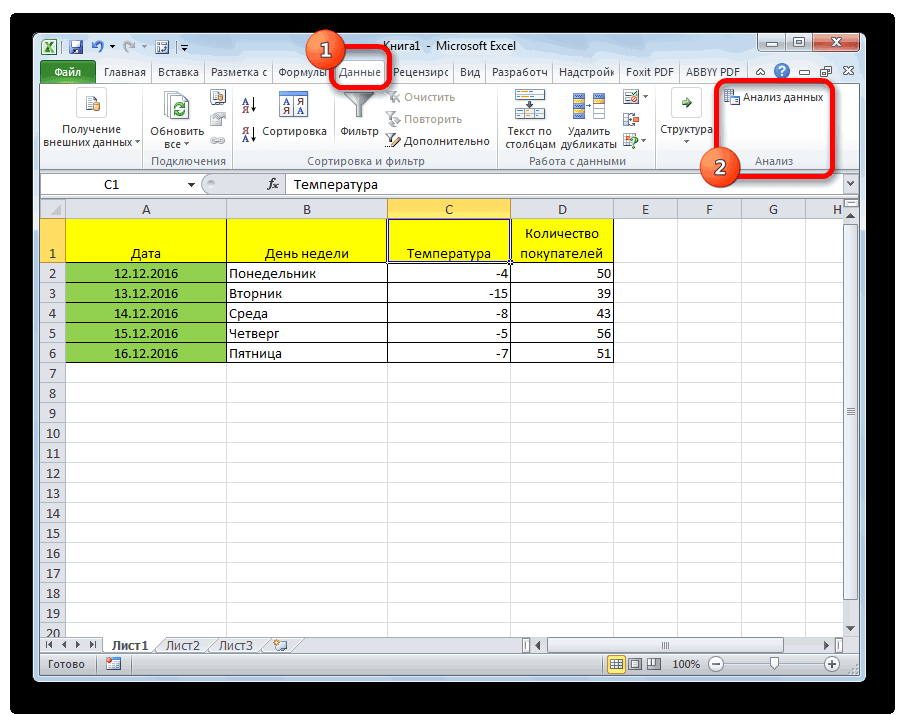
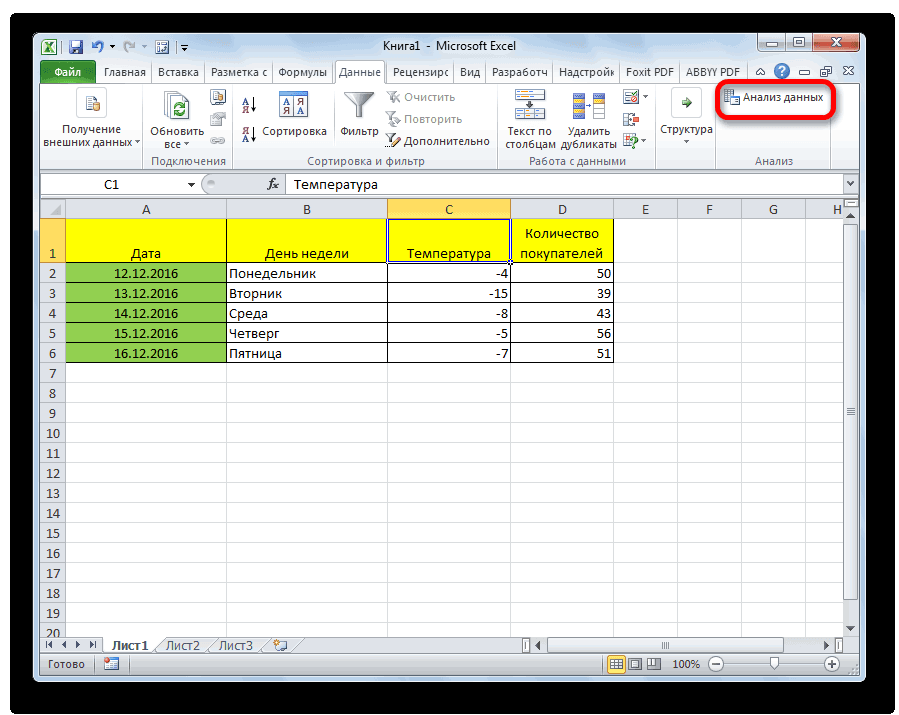
Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее.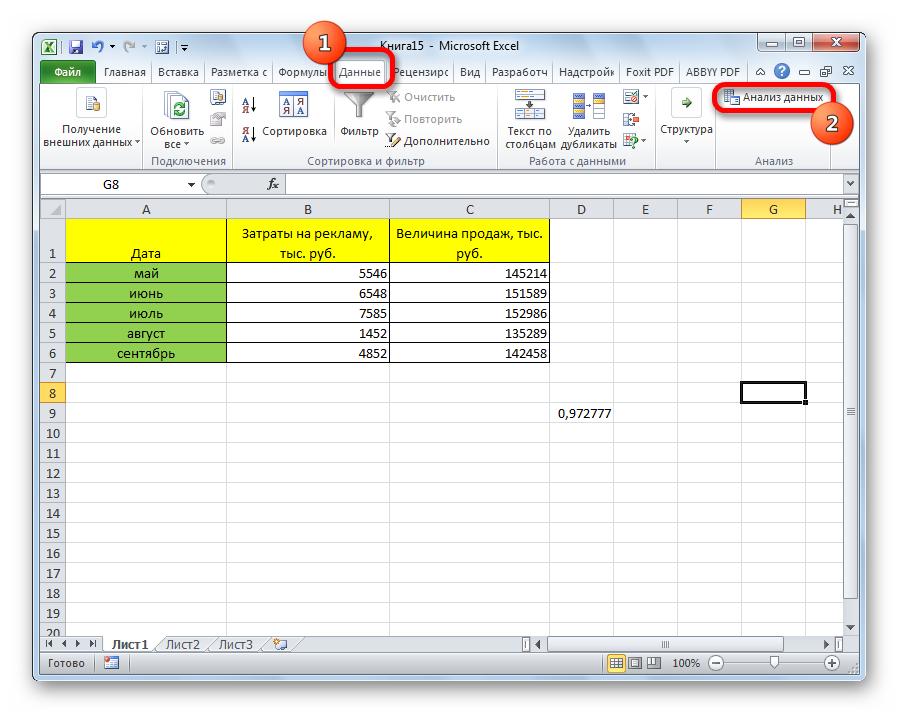 
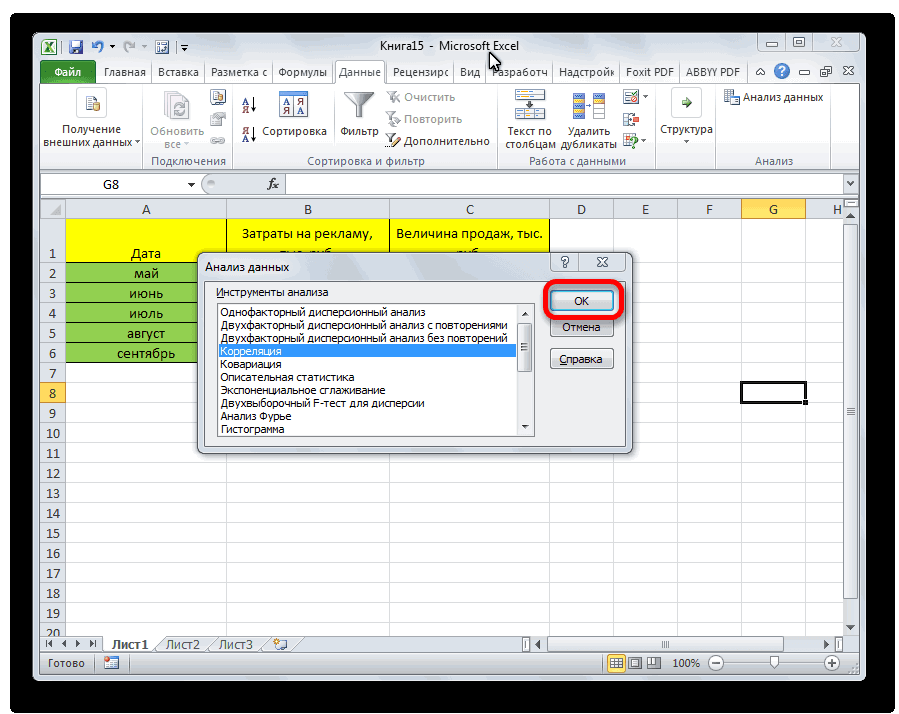
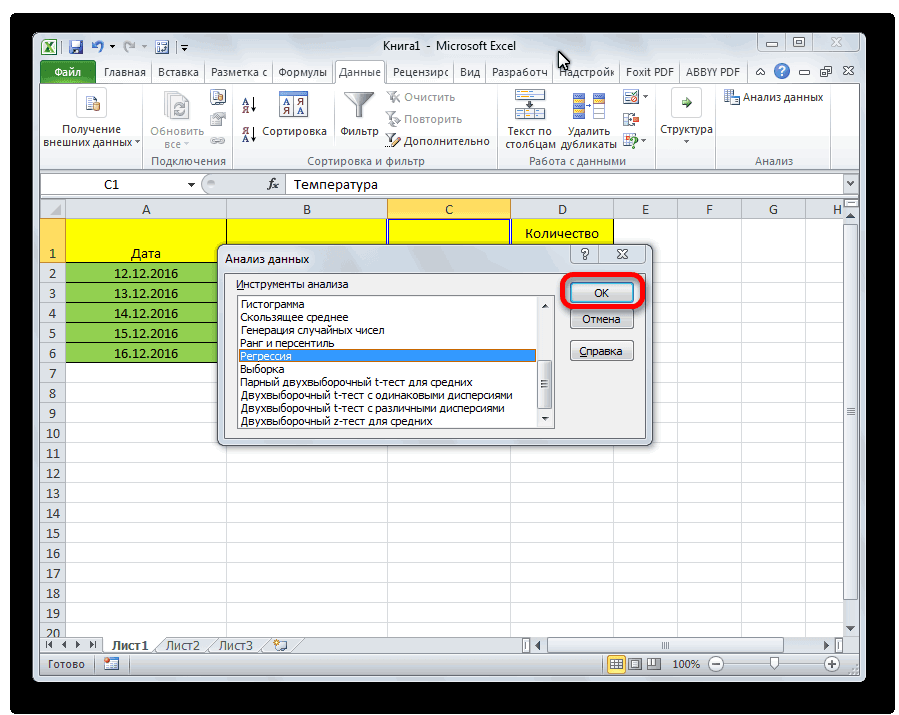
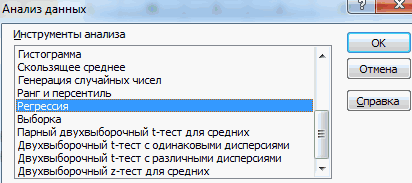
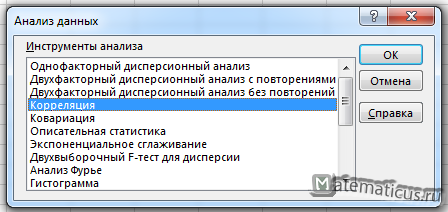
Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК».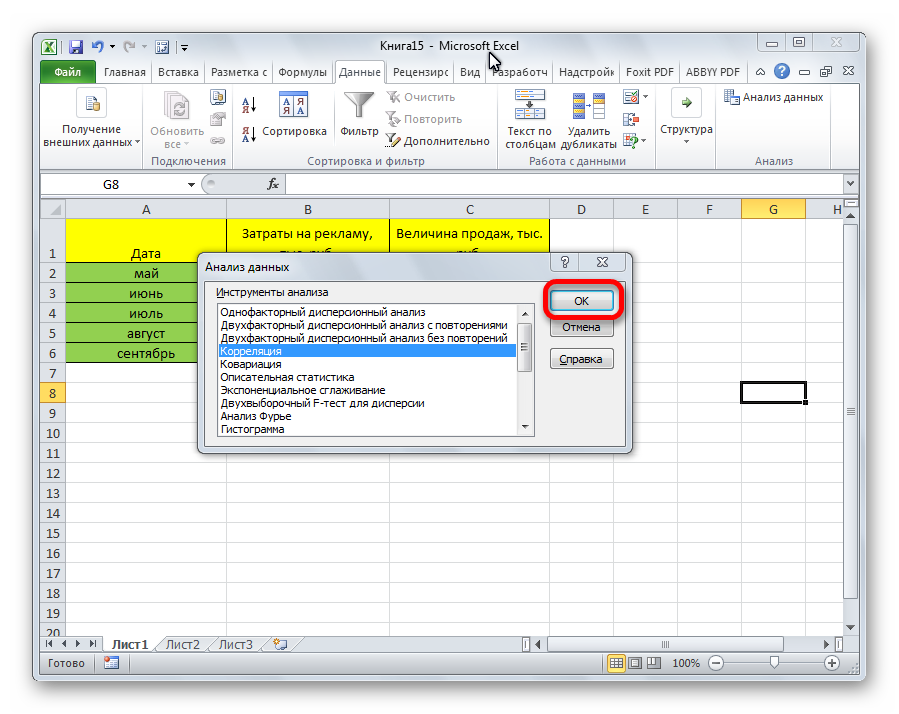 
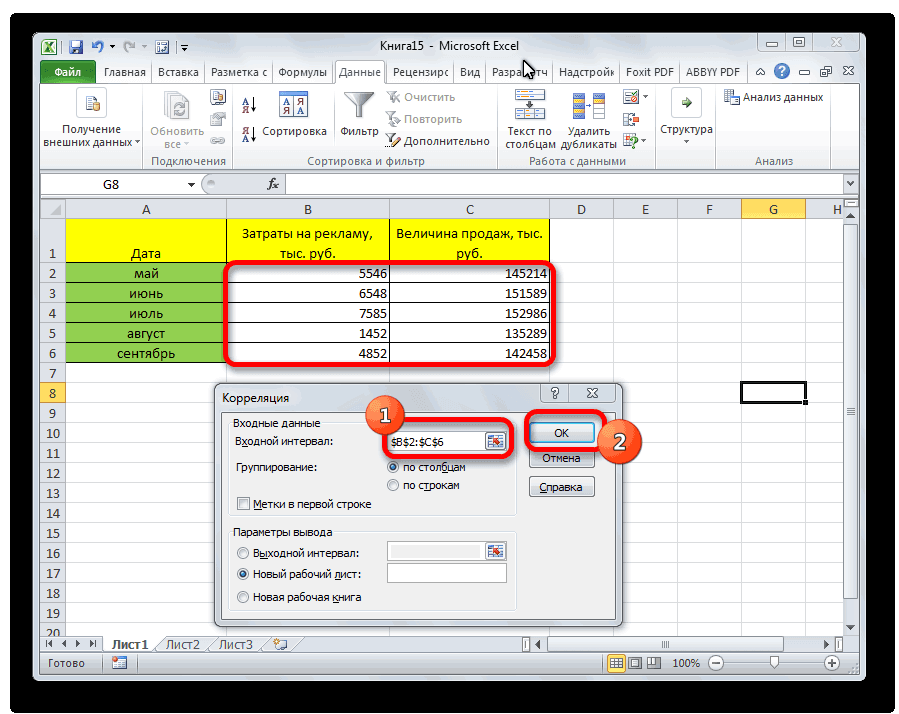
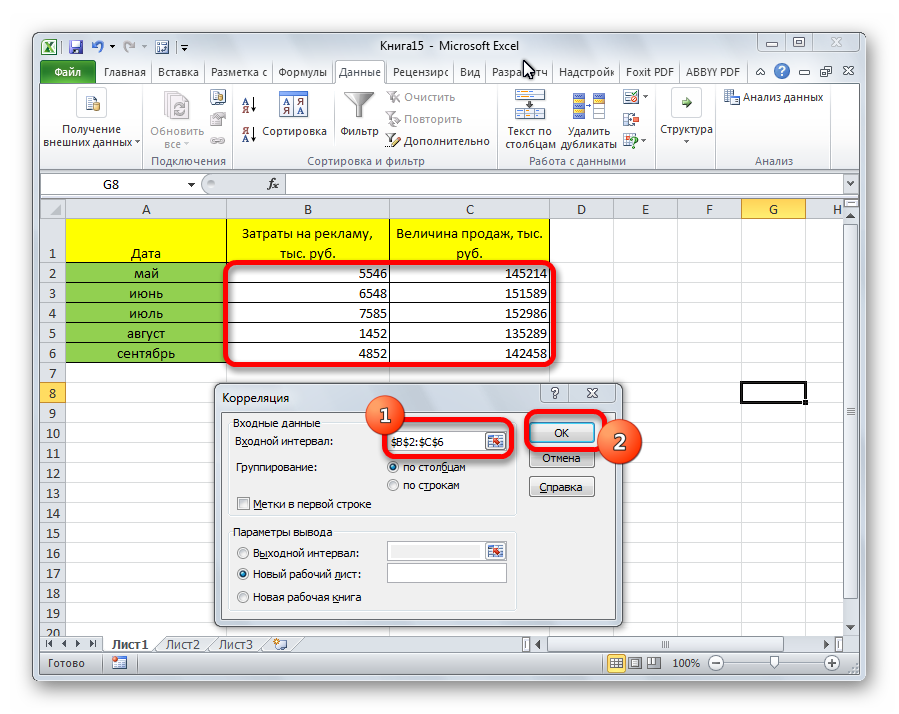
Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».
Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».
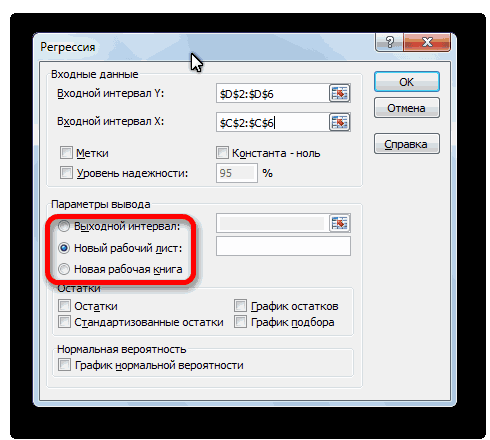
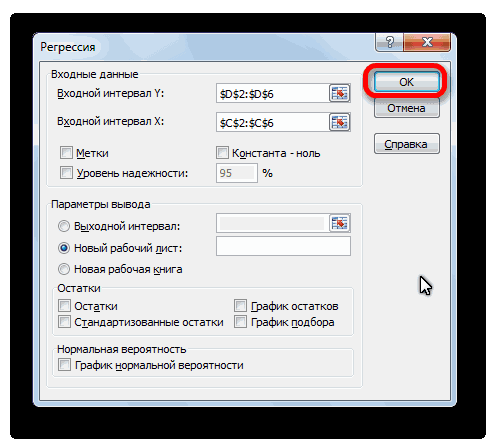
В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».
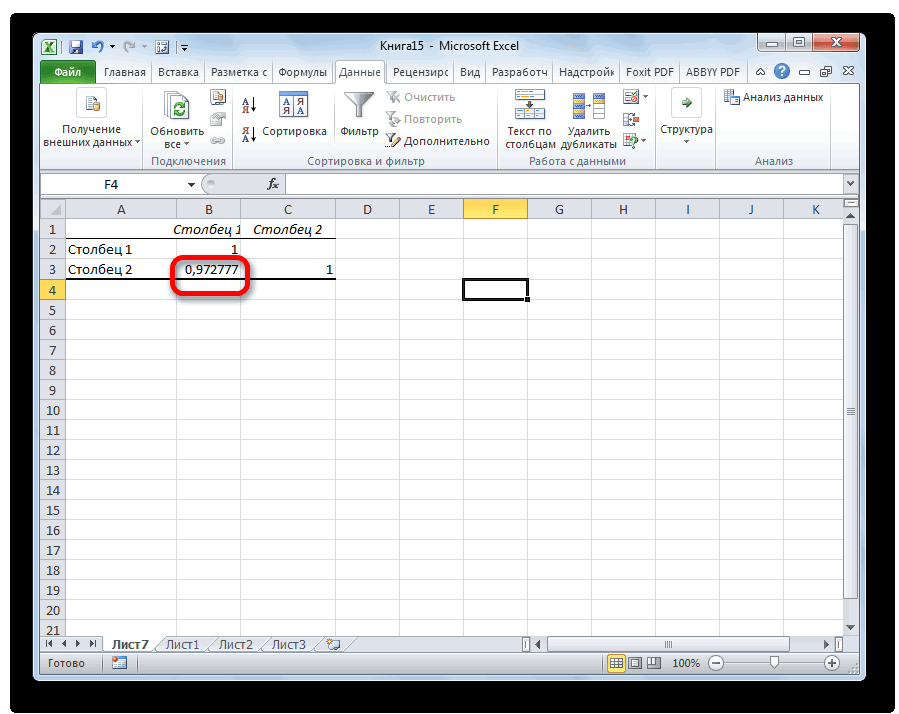
Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более.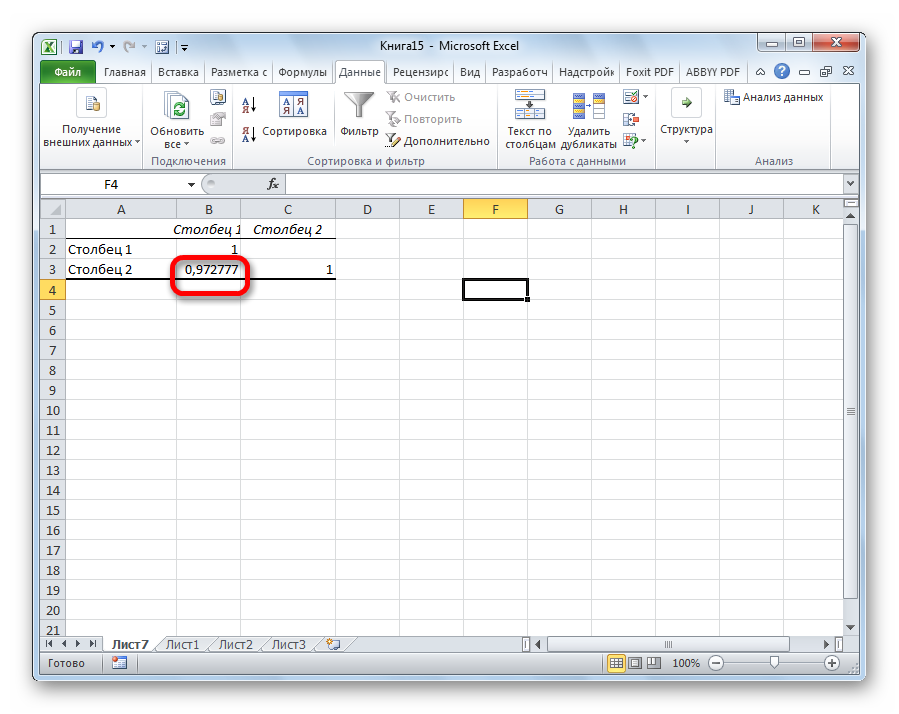 
Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.
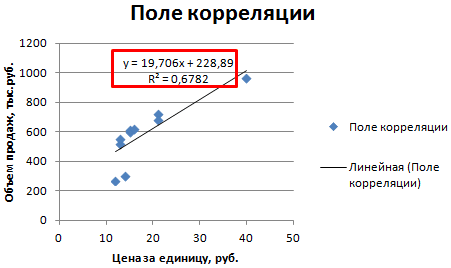
Как построить поле корреляции в Excel
Итак, давайте теперь разберемся, как построить поле корреляции. Для начала нужно разобраться, что это вообще такое. Под корреляционным полем подразумевается фактически график корреляции. Главное требование к такой диаграмме – каждая точка должна соответствовать единице совокупности. Поле корреляции поможет установить более глубокие связи и проанализировать данные более качественно. Для начала нам нужно найти коэффициент корреляции между двумя диапазонами, используя функцию КОРРЕЛ.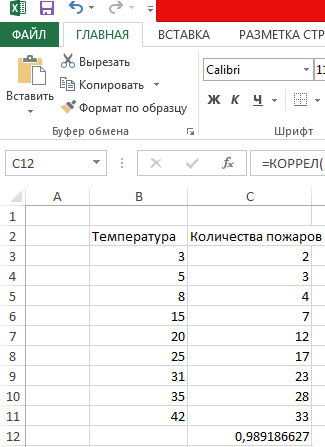 
После того, как мы это сделали, мы теперь можем сделать поле корреляции. Для этого выполняем следующие действия:
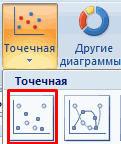
- Переходим во вкладку «Вставка» и там находим вариант диаграммы «точечный график».
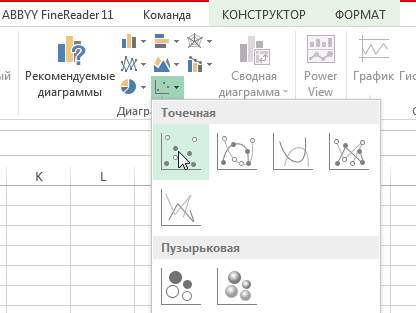
- После того, как мы его добавили, нажимаем по будущему полю корреляции правой кнопкой мыши и вызываем контекстное меню. Далее нажимаем на «Выбрать данные».
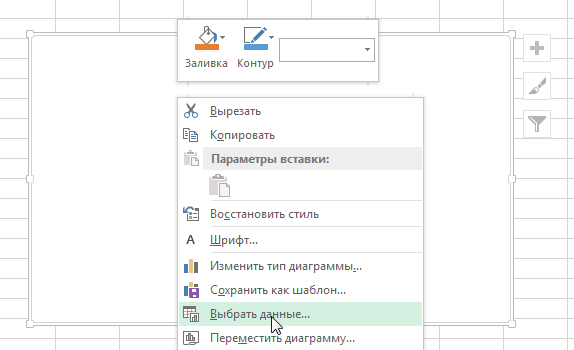
- Далее выбираем наш диапазон в качестве источника данных. После этого подтверждаем свои действия нажатием клавиши ОК. Все остальные действия программа выполнит самостоятельно.
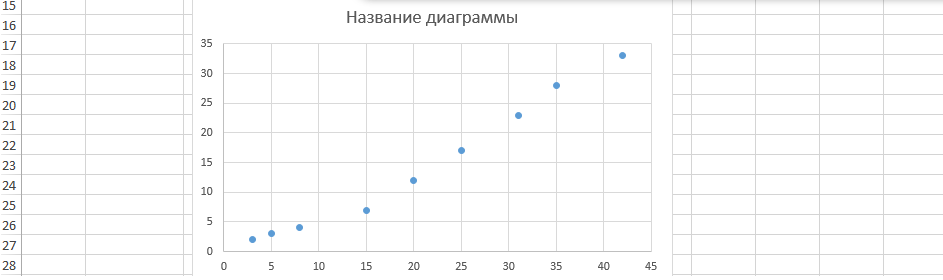
Этот график можно построить не только на основе корреляции, определенной через функцию КОРРЕЛ.
Диаграмма рассеивания. Поле корреляции
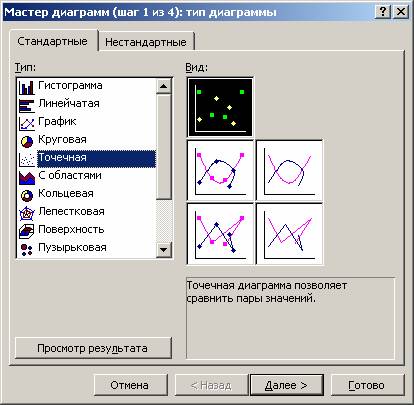
До сих пор часть пользователей сидит на старой версии Word. Как построить корреляционное поле в этом случае? Для этого существует специальный инструмент, который называется мастером диаграмм. Найти его можно на панели инструментов по специфическому изображению диаграммы. Если навести на эту иконку мышкой, то появится всплывающая подсказка, которая поможет нам убедиться в том, что это действительно мастер диаграмм.
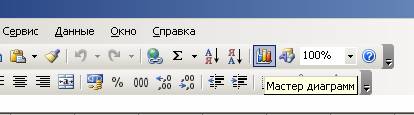
После этого появится диалоговое окно, в котором нам надо выбрать точечный тип диаграммы. Видим, что логика действий в старых версиях офисного пакета в целом остается той же самой, просто немного другой интерфейс. Немного правее мы можем увидеть, как будет выглядеть точечная диаграмма и выбрать подходящий вид, а также прочитать описание этого типа диаграммы. После этого нажимаем на кнопку «Далее».
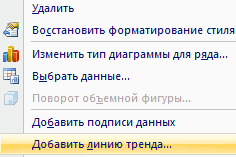
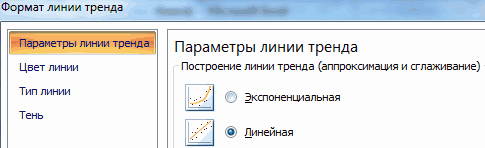
Затем выбираем диапазон данных, и наша линия появляется. После этого можно добавить линию регрессии к графику. Для этого необходимо сделать клик правой кнопкой мыши по одной из точек и в появившемся перечне найти «Добавить линию тренда» и сделать клик по этому пункту.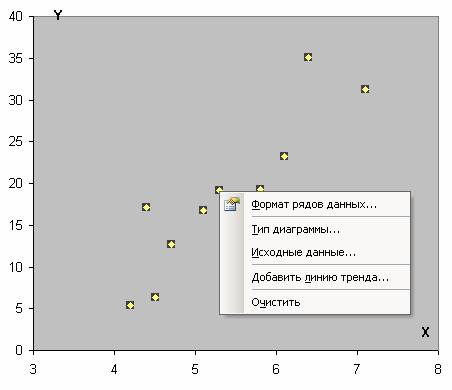 
Далее выставляем настройки. Нас интересует тип «Линейная», а в окне параметров нужно поставить флажок «Показывать уравнение на диаграмме».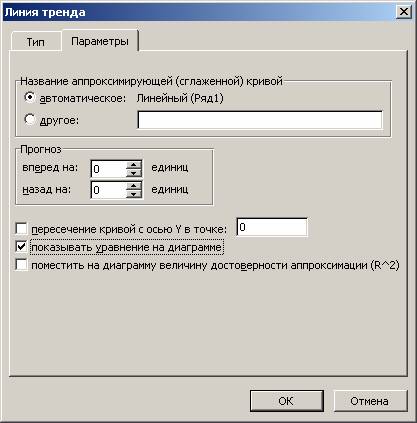
После подтверждения действий у нас появится что-то типа такого графика.
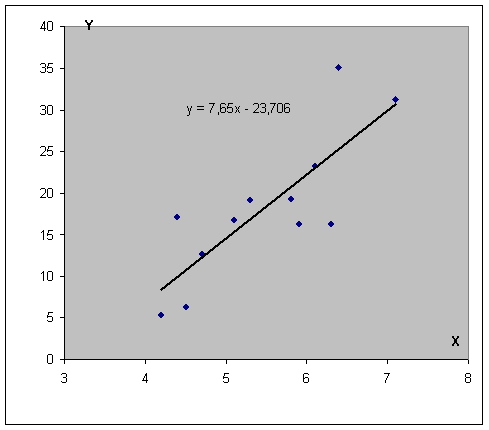
Как видим, возможных вариантов построения может быть огромное количество.
Оцените качество статьи. Нам важно ваше мнение:
Skip to content
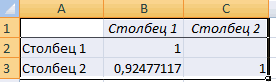
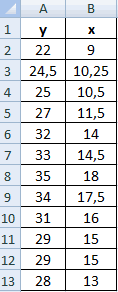
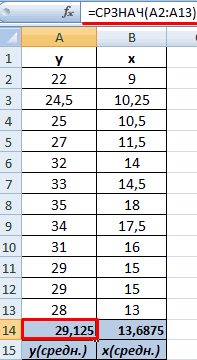
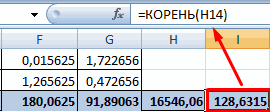
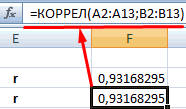
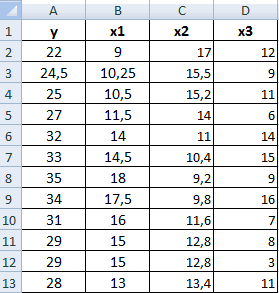
Корреляцию в Excel можно найти по формуле:
=КОРРЕЛ(B3:B11;C3:C11)
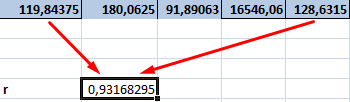
Результат показан ниже
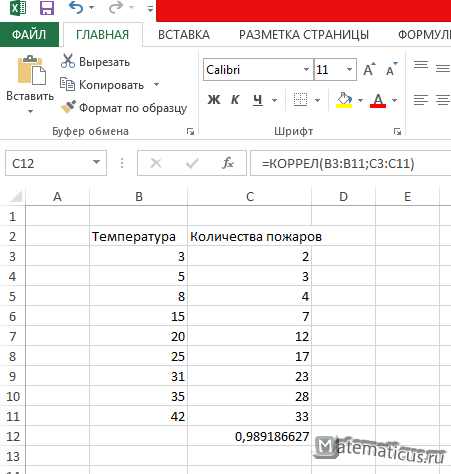
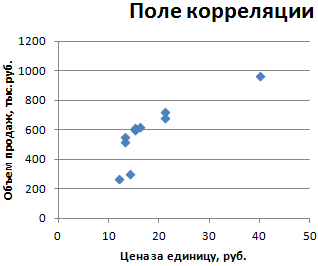
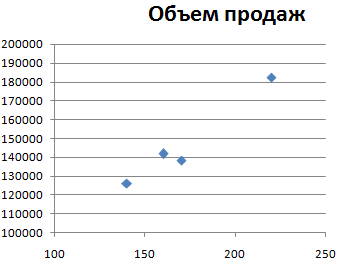
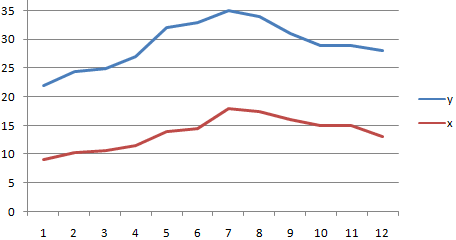
Также можно построить график поля корреляции
Для этого, переходим на вкладку Вставка в области диаграммы выбираем точечный график
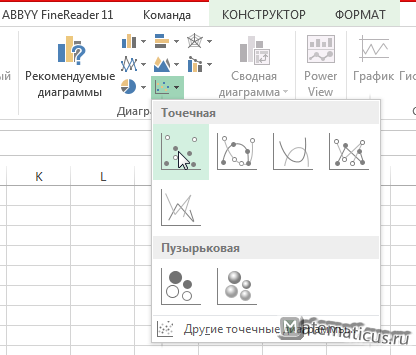
затем переходим на область графика
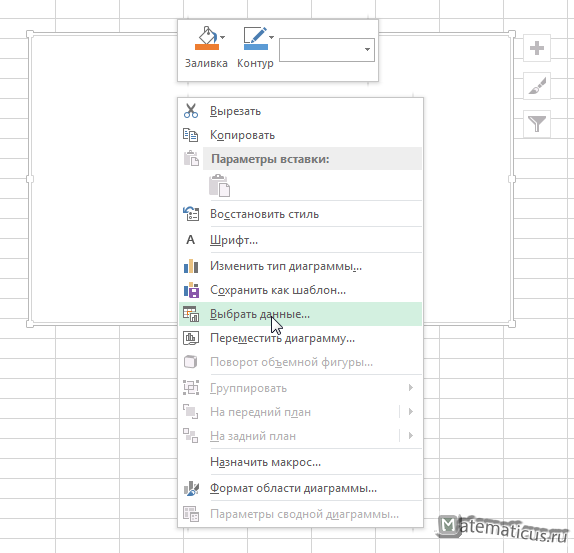
и выбираем данные из диапазона B3:C11, затем Ок. В итоги получаем график поля корреляции по точкам
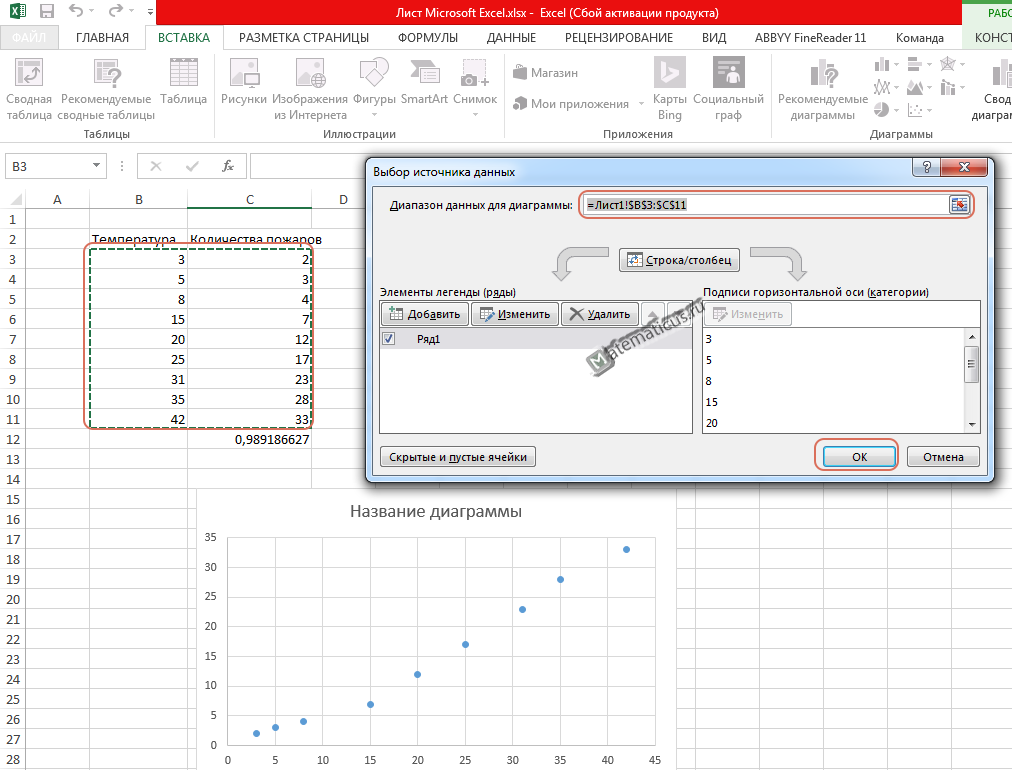
Также быстро корреляцию можно найти через анализ данных
Вкладка Данные, затем Анализ данных. Если у вас эта вкладка не отображается в Excel, то см. здесь как сделать надстройку.
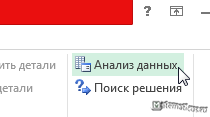
Выбираем корреляцию и жмём Ок.
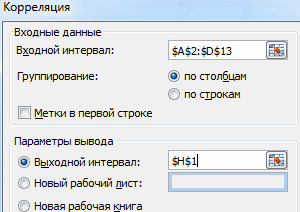
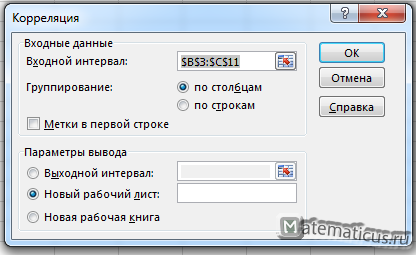
Такой же выбираем диапазон данных, как и ранее делали
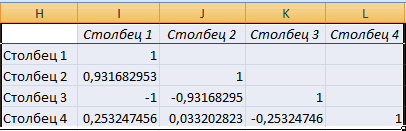
В результате получаем отчёт
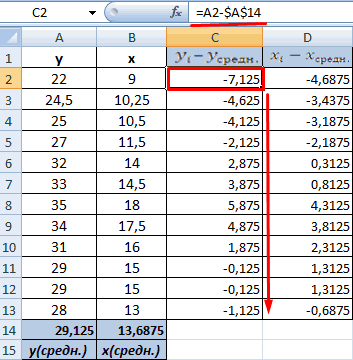
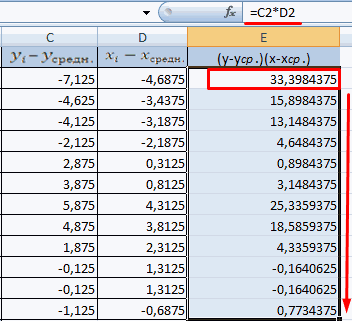
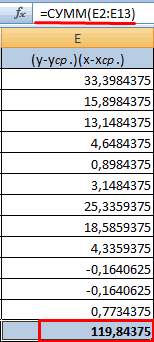
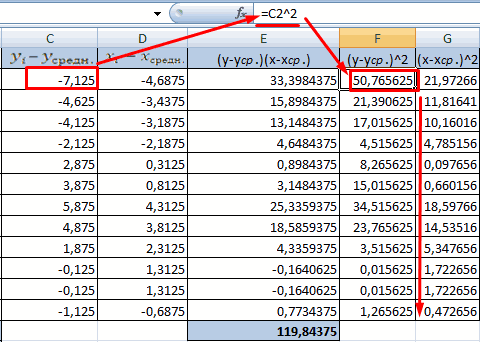
Аналитически, корреляция определяется по формуле:
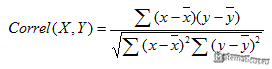
9969
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
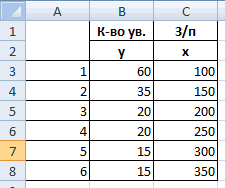
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
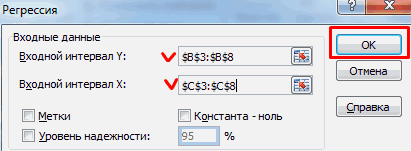
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
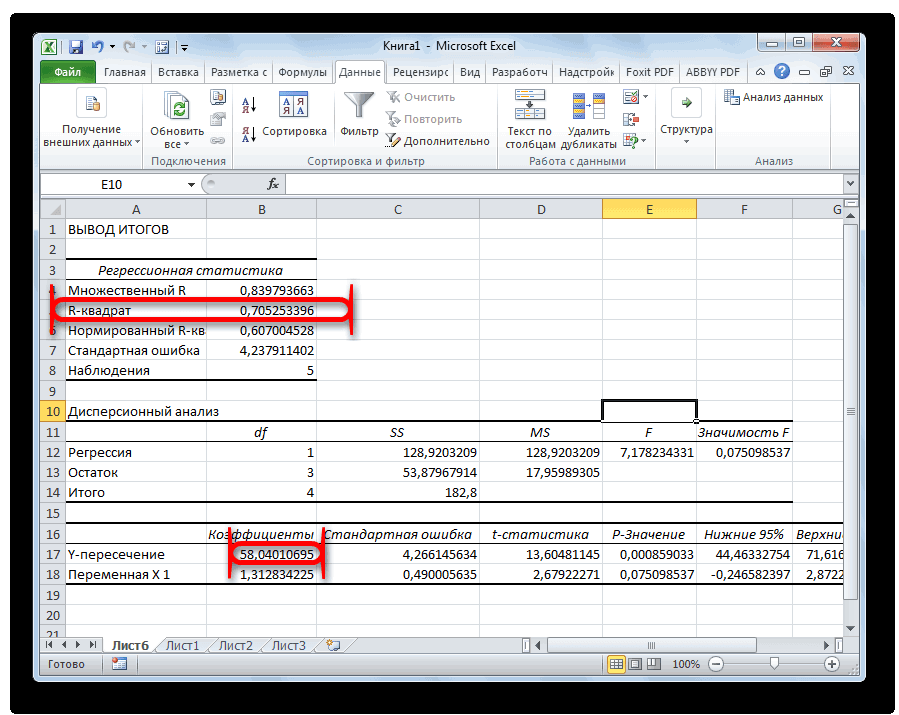
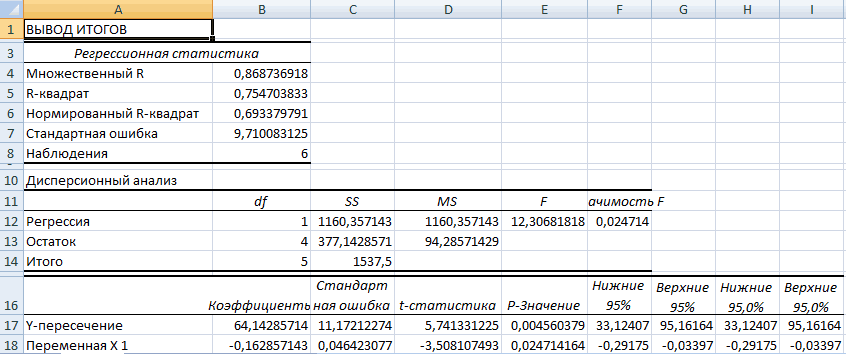
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
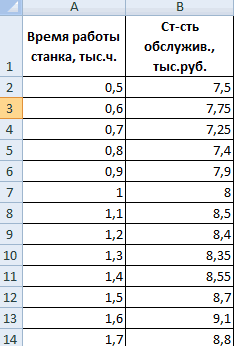
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
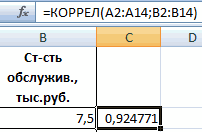
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Correlation basically means a mutual connection between two or more sets of data. In statistics bivariate data or two random variables are used to find the correlation between them. Correlation coefficient is generally the measurement of correlation between the bivariate data which basically denotes how much two random variables are correlated with each other.
If the correlation coefficient is 0, the bivariate data are not correlated with each other.
If the correlation coefficient is -1 or +1, the bivariate data are strongly correlated with each other.
r=-1 denotes strong negative relationship and r=1 denotes strong positive relationship.
In general, if the correlation coefficient is close to -1 or +1 then we can say that the bivariate data are strongly correlated to each other.
The correlation coefficient is calculated using Pearson’s Correlation Coefficient which is given by :
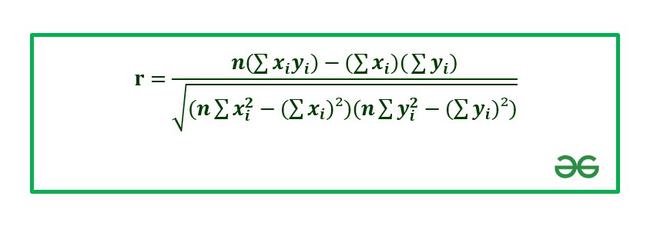
where,
r : Correlation coefficient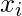
where,
r : Correlation coefficient: Values of the variable y. n : Number of samples taken in the data set. Numerator : Covariance of x and y. Denominator : Product of Standard Deviation of x and Standard Deviation of y.
In this article we are going to discuss how to make correlation charts in Excel using suitable examples.
Example 1 : Consider the following data set :
FINDING CORRELATION COEFFICIENT IN EXCEL
In Excel to find the correlation coefficient use the formula :
=CORREL(array1,array2) array1 : array of variable x array2: array of variable yTo insert array1 and array2 just select the cell range for both.
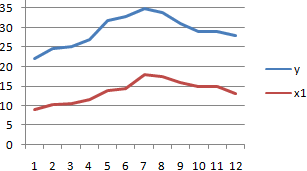
1. Let’s find the correlation coefficient for the variables and X and Y1.
array1 : Set of values of X. The cell range is from A2 to A6.
array2 : Set of values of Y1. The cell range is from B2 to B6.
Similarly, you can find the correlation coefficients for (X , Y2) and (X , Y3) using the Excel formula.
Finally, the correlation coefficients are as follows :
From the above table we can infer that :
X and Y1 has negative correlation coefficient.
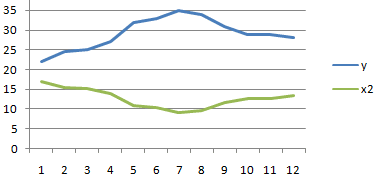
X and Y2 has positive correlation coefficient.
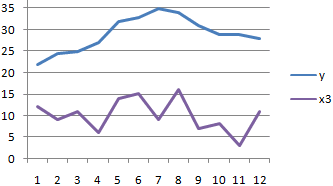
X and Y3 are not correlated as the correlation coefficient is almost zero.
Correlation Chart in Excel:
A scatter plot is mostly used for data analysis of bivariate data. The chart consists of two variables X and Y where one of them is independent and the second variable is dependent on the previous one. The chart is a pictorial representation of how these two data are correlated with each other. Three cases are possible on the basis of the value of the correlation coefficient, R as shown below :
Types of Correlation Chart
Example 2: Consider the following data set :
The correlation coefficients for the above data set are :
The steps to plot a correlation chart are :
- Select the bivariate data X and Y in the Excel sheet.
- Go to Insert tab on the top of the Excel window.
- Select Insert Scatter or Bubble chart. A pop-down menu will appear.
- Now select the Scatter chart.
- Now, we need to add a linear trendline in the scatter plot to show the correlation between the bivariate data. In order to do so, select the chart and from the top right corner click on the “+” button and then check the box of Trendline.
- The trendline is now added and our correlation chart is now ready.
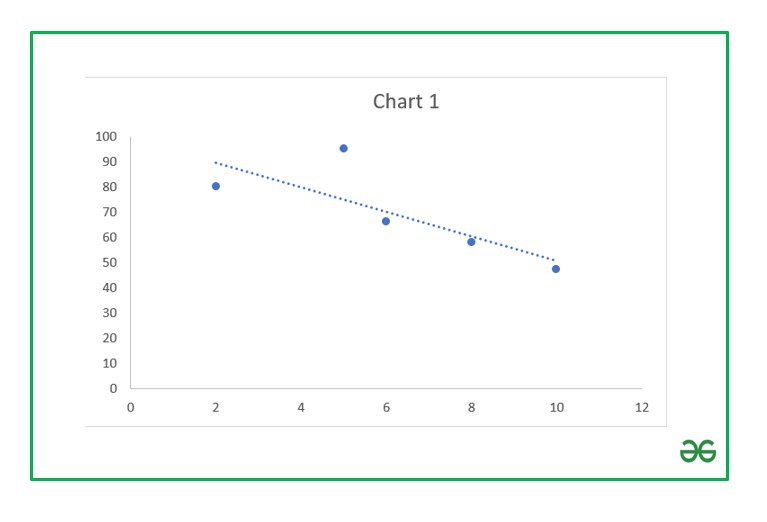
Negative relationship chart
- Now you can format the Trendline by selecting and clicking on the “Format Trendline” option. A dialog box will open where you can change the type and color of the trendline and also show the
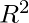: Values of the variable y.
n : Number of samples taken in the data set.
Numerator : Covariance of x and y.
Denominator : Product of Standard Deviation of x and Standard Deviation of y.
In this article we are going to discuss how to make correlation charts in Excel using suitable examples.
Example 1 : Consider the following data set :
FINDING CORRELATION COEFFICIENT IN EXCEL
In Excel to find the correlation coefficient use the formula :
=CORREL(array1,array2) array1 : array of variable x array2: array of variable y
To insert array1 and array2 just select the cell range for both.
1. Let’s find the correlation coefficient for the variables and X and Y1.
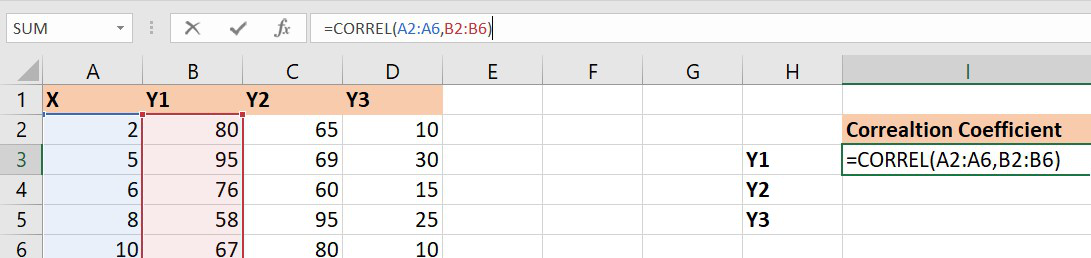
array1 : Set of values of X. The cell range is from A2 to A6.
array2 : Set of values of Y1. The cell range is from B2 to B6.
Similarly, you can find the correlation coefficients for (X , Y2) and (X , Y3) using the Excel formula.
Finally, the correlation coefficients are as follows :
From the above table we can infer that :
X and Y1 has negative correlation coefficient.
X and Y2 has positive correlation coefficient.
X and Y3 are not correlated as the correlation coefficient is almost zero.
Correlation Chart in Excel:
A scatter plot is mostly used for data analysis of bivariate data. The chart consists of two variables X and Y where one of them is independent and the second variable is dependent on the previous one. The chart is a pictorial representation of how these two data are correlated with each other. Three cases are possible on the basis of the value of the correlation coefficient, R as shown below :
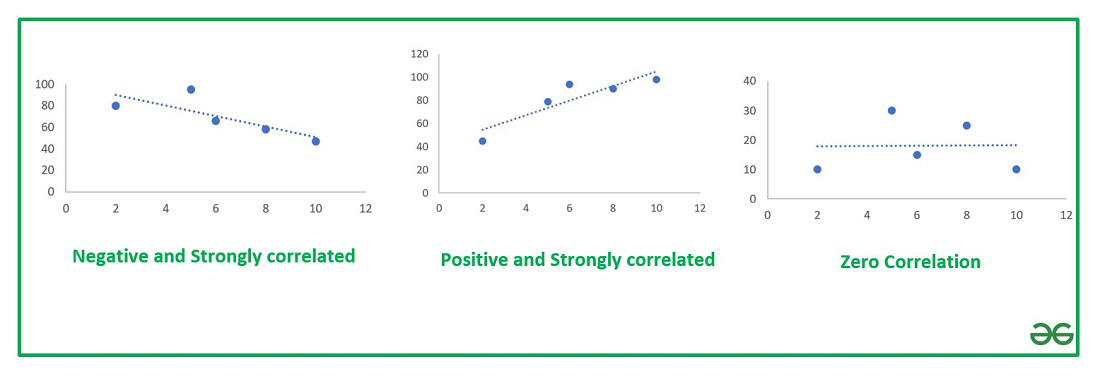
Types of Correlation Chart
Example 2: Consider the following data set :
The correlation coefficients for the above data set are :
The steps to plot a correlation chart are :
- Select the bivariate data X and Y in the Excel sheet.
- Go to Insert tab on the top of the Excel window.
- Select Insert Scatter or Bubble chart. A pop-down menu will appear.
- Now select the Scatter chart.
- Now, we need to add a linear trendline in the scatter plot to show the correlation between the bivariate data. In order to do so, select the chart and from the top right corner click on the “+” button and then check the box of Trendline.
- The trendline is now added and our correlation chart is now ready.
Negative relationship chart
- Now you can format the Trendline by selecting and clicking on the “Format Trendline” option. A dialog box will open where you can change the type and color of the trendline and also show the 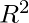value in the chart.
You can further format the above chart by making it more interactive by changing the “Chart Styles”, adding suitable “Axis Titles”, “Chart Title”, “Data Labels”, changing the “Chart Type” etc. It can be done using the “+” button in the top right corner of the Excel chart.
Finally, after all the modification the charts look like :
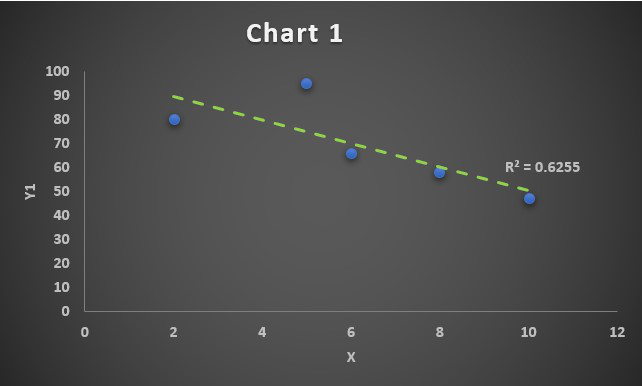
Correlation Chart 1
Since the correlation coefficient is R=-0.79, we have obtained a negative correlated chart. The linear trendline will grow downwards.
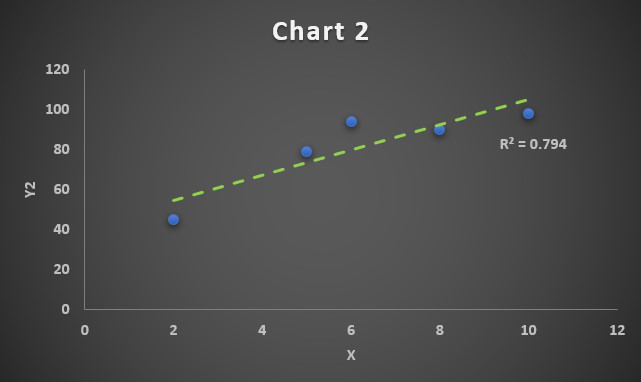
Correlation Chart 2
Since the correlation coefficient is R=0.89, we have obtained a positive correlated chart. The linear trendline will grow upwards.
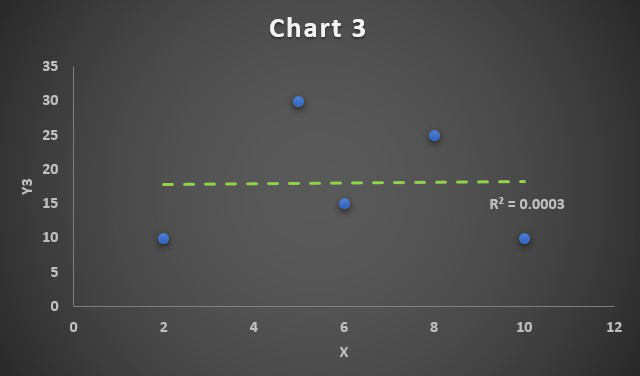
Correlation Chart 3
Since the correlation coefficient is R=0.01, which is approximately 0, so we have obtained a zero correlated chart. The linear trendline will be a straight line parallel to X-axis and it implies the bivariate data X and Y3 are not correlated to each other.
Last Updated :
23 Jun, 2021
Like Article
Save Article
Excel — это мощный инструмент для обработки данных. Он используется в бизнесе и научных исследованиях, где необходимо анализировать, сравнивать и обрабатывать большие объемы данных. Одним из способов анализа данных в Excel является построение поля корреляции.
Поле корреляции — это график, который показывает связь между двумя наборами данных. Он помогает определить, насколько сильно связаны два набора данных. В Excel построение поля корреляции легко выполнить при помощи нескольких простых шагов.
В этой статье мы рассмотрим пошаговую инструкцию по построению поля корреляции в Excel. Мы покажем, как выбрать данные для анализа, как настроить график и как интерпретировать результаты. Если вы начинающий пользователь Excel или просто хотите узнать больше о построении поля корреляции, эта статья для вас.
Содержание
- Построение поля корреляции в Excel
- Шаг 1: Установка Excel
- Шаг 2: Выбор набора данных
- Подготовка данных для анализа
- Шаг 3:
- Шаг 4: Создание поля корреляции
- Шаг 5: Интерпретация результата
- Вопрос-ответ
- Как построить поле корреляции в Excel?
- Как интерпретировать поле корреляции?
- Можно ли построить поле корреляции для большого количества данных?
- Как определить степень силы корреляции по полю корреляции?
- Как использовать поле корреляции в анализе данных?
Построение поля корреляции в Excel
Один из методов анализа сильных и слабых связей между переменными является построение поля корреляции или матрицы корреляции в Excel. Это позволяет не только проанализировать взаимосвязь, но и оценить ее величину.
Для построения поля корреляции необходимо иметь набор данных, представленных в таблице Excel. Каждая переменная должна иметь свой столбец, а каждый объект должен быть представлен в строке, набор данных должен быть достаточно большим, чтобы можно было провести анализ взаимосвязи между переменными.
Для создания матрицы корреляции в Excel необходимо выбрать вкладку «Данные» и затем выбрать «Анализ данных». В открывшемся окне необходимо выбрать «Корреляция» и затем выбрать таблицу с данными. После этого нужно сохранить результаты анализа в новый лист и нажать «ОК».
Для визуализации поля корреляции можно использовать специальные графики, которые позволяют визуально оценить силу и направление связей между переменными. Например, можно использовать диаграмму рассеяния или график линейной регрессии.
Шаг 1: Установка Excel
Первым шагом для построения поля корреляции в Excel является установка самих приложений.
Приложение Excel является компьютерной программой, которая позволяет обрабатывать и анализировать данные с помощью таблиц и графиков. Оно может быть установлено на ПК или ноутбук.
Если у вас еще нет Microsoft Office, включающего Excel, можно купить его на официальном сайте Microsoft. Также можно воспользоваться пробной версией на 30 дней, чтобы опробовать приложение перед покупкой.
Для установки Excel на компьютер, нужно выполнить следующие действия:
- Скачать установочный файл с официального сайта Microsoft
- Запустить установку и следовать инструкциям на экране
- Дождаться завершения установки
После установки Excel можно начинать работать с таблицами и графиками, в частности, строить поле корреляции.
Шаг 2: Выбор набора данных
Для построения поля корреляции необходимо выбрать набор данных, на основе которого будет проводиться анализ. Выбор данных должен быть обоснованным и иметь ясную цель. Например, если вы хотите проанализировать взаимосвязь между температурой и количеством проданных мороженых за месяц, то необходимо выбрать данные, содержащие информацию о температуре и продажах за каждый месяц. Важно убедиться, что данные соответствуют рассматриваемому временному интервалу и не содержат пропусков или ошибок.
При выборе набора данных следует также учитывать его объем и доступность. Если у вас есть опыт работы с Excel, вы можете использовать уже готовые наборы данных, которые могут быть найдены в интернете или внутри Excel. Если же вы работаете с данными, полученными из других источников, то необходимо убедиться, что они сохранены в формате, поддерживаемом Excel.
Важно отметить, что выбор набора данных должен происходить в соответствии с целью анализа и учитывать объем и доступность данных. Только так можно получить точные и корректные результаты.
Подготовка данных для анализа
Шаг 3:
Перед тем, как начать построение поля корреляции в Excel, необходимо подготовить данные для анализа. Один из основных этапов подготовки — проверка качества данных и их очистка от ошибок и выбросов.
Если в данных есть пропущенные значения, необходимо решить, как с ними поступить. Можно удалить строки или столбцы с пропущенными значениями, можно заменить их на среднее или медианное значение по соответствующему столбцу. Важно помнить, что выбор метода должен быть обоснован и зависит от конкретной задачи анализа данных.
Также необходимо проверить данные на наличие ошибок и выбросов. Если в данных есть некорректные значения, то они могут сильно исказить результаты анализа. Поэтому необходимо удалить ошибки или попытаться их исправить. Если в данных есть выбросы, то их также необходимо удалить или попытаться объяснить физической или биологической природой явления.
Важно помнить, что корректные и качественные данные — залог успешного анализа и построения поля корреляции в Excel.
Шаг 4: Создание поля корреляции
После того, как были выбраны соответствующие данные и рассчитаны коэффициенты корреляции, можно приступать к построению поля корреляции в Excel.
Для начала необходимо выделить ячейки, в которые будет вставлено поле корреляции. Затем, выбрав вкладку «Вставка», необходимо найти и выбрать опцию «Диаграмма рассеяния».
В появившемся окне необходимо выбрать опцию «Диаграмма рассеяния с линиями тренда», затем нажать кнопку «Создать».
После этого, на графике необходимо выбрать опцию «Множественная корреляция», чтобы поле корреляции было построено и отображено на графике.
Подписи графика можно изменить, добавив названия вертикальной и горизонтальной осей, а также добавив заголовок графика. Для этого необходимо выбрать график и выбрать опцию «Оформление», а затем выбрать нужный пункт меню.
Шаг 5: Интерпретация результата
После того, как вы построили поле корреляции в Excel, необходимо правильно интерпретировать его результаты. Одним из главных инструментов для анализа корреляции является коэффициент корреляции Пирсона.
Коэффициент корреляции Пирсона показывает, как сильно связаны между собой две переменные. Значение коэффициента может находиться от -1 до 1. Если значение близко к 1, то это говорит о сильной прямой связи, а если близко к -1, то о сильной обратной связи. Значение коэффициента равное 0, говорит о том, что между переменными нет связи.
Для того, чтобы принять решение на основе коэффициента корреляции Пирсона, необходимо обратить внимание не только на его значение, но и на соответствующий ему уровень значимости. Обычно, если уровень значимости меньше 0,05, то связь между переменными считается статистически значимой, что означает, что эта связь не случайна.
- Пример: Если вы построили поле корреляции между ростом и весом людей, то коэффициент корреляции Пирсона покажет, насколько эти переменные связаны. Если значение коэффициента будет равно 0,8 и уровень значимости меньше 0,05, то можно сделать вывод, что рост и вес сильно связаны между собой. Это означает, что если рост человека выше, то скорее всего у него будет также и больший вес.
Таким образом, правильная интерпретация результата поле корреляции в Excel поможет принять обоснованное решение на основе данных и провести анализ связей между переменными.
Вопрос-ответ
Как построить поле корреляции в Excel?
Для построения поля корреляции в Excel необходимо выбрать данные, которые будут сравниваться, затем нажать на вкладку «Вставка», выбрать «Диаграммы рассеяния» и нажать на «Диаграмма рассеяния с линией тренда и полем корреляции». После этого появится поле корреляции.
Как интерпретировать поле корреляции?
Поле корреляции показывает коэффициент корреляции между выбранными данными. Коэффициент корреляции может принимать значения от -1 до 1. Значения близкие к -1 означают обратную корреляцию, близкие к 0 – отсутствие корреляции и близкие к 1 – прямую корреляцию между данными.
Можно ли построить поле корреляции для большого количества данных?
Да, можно. Однако при большом количестве данных поле корреляции может оказаться нечитабельным. В этом случае рекомендуется разбивать данные на группы и строить поле корреляции для каждой группы.
Как определить степень силы корреляции по полю корреляции?
Степень силы корреляции можно определить по значению коэффициента корреляции. Если значение коэффициента корреляции близко к -1 или 1, то корреляция сильная. Если значение коэффициента корреляции близко к 0, то корреляция слабая или отсутствует.
Как использовать поле корреляции в анализе данных?
Поле корреляции позволяет выявлять связи между данными. Например, если мы строим поле корреляции между количеством продаж и рекламными затратами, то мы можем выявить, насколько сильно рекламные затраты влияют на количество продаж. Это позволяет принимать более обоснованные решения при планировании рекламных кампаний и управлении продажами.
2 способа корреляционного анализа в Microsoft Excel
Correlation Chart 1
Since the correlation coefficient is R=-0.79, we have obtained a negative correlated chart. The linear trendline will grow downwards.
Correlation Chart 2
Since the correlation coefficient is R=0.89, we have obtained a positive correlated chart. The linear trendline will grow upwards.
Correlation Chart 3
Since the correlation coefficient is R=0.01, which is approximately 0, so we have obtained a zero correlated chart. The linear trendline will be a straight line parallel to X-axis and it implies the bivariate data X and Y3 are not correlated to each other.
Last Updated :
23 Jun, 2021
Like Article
Save Article
