Использование статистических методов может помочь в анализе больших объемов данных для выявления закономерностей и зависимостей. Ранговая корреляция Спирмена — это один из способов оценки статистической связи между двумя переменными. Она великолепно подходит для работы с данными без явной линейной связи.
Microsoft Excel предоставляет возможность расчета ранговой корреляции Спирмена для данных, которые могут быть легко подготовлены с помощью этой программы. Чтобы использовать данную функцию, необходимо знать, какие данные можно использовать и как ее правильно применять.
В этой статье мы рассмотрим, как работать с ранговой корреляцией Спирмена в программе MS Excel. Мы покажем, как подготовить данные и выполнить расчеты, чтобы получить точную оценку статистической связи. Также мы расскажем о том, как интерпретировать результаты и использовать их для принятия решений в своей работе или исследованиях.
Если вы хотите узнать больше о том, как использовать ранговую корреляцию Спирмена в MS Excel, то этот материал для вас. Давайте начнем!
Содержание
- Ранговая корреляция Спирмена в MS Excel
- Что такое ранговая корреляция Спирмена?
- Как использовать ранговую корреляцию Спирмена в MS Excel?
- Что такое ранговая корреляция Спирмена?
- Применение ранговой корреляции Спирмена в MS Excel
- Что такое ранговая корреляция Спирмена?
- Как использовать ранговую корреляцию Спирмена в MS Excel?
- Как интерпретировать результаты?
- Шаги использования ранговой корреляции Спирмена в MS Excel
- Шаг 1: Подготовьте данные
- Шаг 2: Расположите данные
- Шаг 3: Выберите функцию корреляции
- Шаг 4: Укажите данные для анализа
- Шаг 5: Выберите уровень значимости
- Шаг 6: Нажмите «ОК»
- Шаг 7: Проверьте результаты
- Интерпретация результатов ранговой корреляции Спирмена в MS Excel
- Вопрос-ответ
- Какая ранжировка используется при расчете ранговой корреляции Спирмена?
- Как выявить наличие корреляции между двумя переменными в Excel?
- Как интерпретировать полученное значение коэффициента ранговой корреляции Спирмена?
- Можно ли использовать ранговую корреляцию Спирмена для большого количества переменных?
- Как понять, что полученный коэффициент корреляции Спирмена статистически значим?
Ранговая корреляция Спирмена в MS Excel
Что такое ранговая корреляция Спирмена?
Ранговая корреляция Спирмена — это метод определения связи между двумя переменным, используя ранги этих переменных. Этот метод подходит для измерения линейных и нелинейных связей между переменными, даже если они не нормально распределены.
Как использовать ранговую корреляцию Спирмена в MS Excel?
Для использования ранговой корреляции Спирмена в MS Excel, первым шагом является подготовка данных, используя ранги переменных. Затем с помощью функции CORREL в Excel можно вычислить ранговую корреляцию Спирмена. Формула функции CORREL имеет следующую структуру: =CORREL(диапазон_рангов_первой_переменной,диапазон_рангов_второй_переменной).
Важно помнить, что ранговая корреляция Спирмена может выдавать значения от -1 (полная отрицательная корреляция) до 1 (полная положительная корреляция). Значение 0 означает, что связь между переменными отсутствует.
Используя ранговую корреляцию Спирмена в Excel, можно определить, насколько сильно связаны две переменные и как изменения одной переменной влияют на другую переменную. Этот метод может быть полезен в различных областях, включая маркетинг, науку о данных, исследования в области здравоохранения и др.
Что такое ранговая корреляция Спирмена?
Ранговая корреляция Спирмена – это метод, используемый для оценивания связи между двумя переменными. Он базируется на ранжировании значений каждой переменной в порядке увеличения. Таким образом, метод рассматривает не значения, а их порядок.
Ранговая корреляция Спирмена измеряется коэффициентом корреляции, который может принимать значение от -1 до 1. Значение -1 означает полную обратную связь, 0 – отсутствие связи, а 1 – полную прямую связь. Чем ближе коэффициент к одному из крайних значений, тем сильнее связь между переменными.
Ранговая корреляция Спирмена может быть использована для любых типов переменных, включая категориальные и номинальные переменные. Он часто используется в исследованиях, чтобы определить, есть ли связь между двумя переменными. Он также может быть полезен при работе с большим объемом данных, когда точность вычислений с использованием других методов может стать проблемой.
Таким образом, ранговая корреляция Спирмена – это мощный инструмент статистического анализа, который позволяет оценить связь между переменными в нелинейных моделях и находить зависимости, которые могут быть упущены другими методами. Он полезен для нахождения связей в больших объемах данных и может использоваться в различных областях, от экономики до медицины и науки о климате.
Применение ранговой корреляции Спирмена в MS Excel
Что такое ранговая корреляция Спирмена?
Ранговая корреляция Спирмена — это статистический метод, используемый для определения силы и направления связи между двумя наборами данных, которые измеряются в ранжированном виде. В простых терминах, это позволяет установить, насколько сильно два набора данных связаны друг с другом, не связываясь с их конкретными значениями.
Как использовать ранговую корреляцию Спирмена в MS Excel?
MS Excel предоставляет встроенную функцию для расчета ранговой корреляции Спирмена. Чтобы использовать эту функцию, необходимо выбрать два набора данных, отсортированных в порядке возрастания или убывания. Затем, необходимо выбрать ячейку, где будет выведен результат, и ввести формулу ‘=CORREL (array1,array2)’, где array1 и array2 — диапазоны ячеек, содержащие первый и второй наборы данных соответственно.
Как интерпретировать результаты?
Результаты ранговой корреляции Спирмена могут быть в диапазоне от -1 до 1. Коэффициент, близкий к 1, указывает на положительную корреляцию, т.е. рост одного набора данных ведет к росту другого. Коэффициент, близкий к -1, указывает на отрицательную корреляцию, т.е. рост одного набора данных ведет к снижению другого. Коэффициент, близкий к 0, указывает на отсутствие корреляции между двумя наборами данных.
Шаги использования ранговой корреляции Спирмена в MS Excel
Шаг 1: Подготовьте данные
Перед использованием ранговой корреляции Спирмена в MS Excel необходимо подготовить данные. Обычно данные должны быть представлены в виде таблицы, где каждая строка представляет собой объект, а каждый столбец – некоторую характеристику этого объекта.
Шаг 2: Расположите данные
Расположите данные в двух столбцах Excel. В первом столбце укажите значения первой переменной, во втором – значения второй переменной.
Шаг 3: Выберите функцию корреляции
Выберите функцию корреляции в MS Excel. Для этого нажмите на вкладку «Данные» в верхней части экрана. Затем выберите «Анализ данных» и «Корреляция». Появится окно «Корреляция», где вам нужно выбрать «Ранговую корреляцию Спирмена».
Шаг 4: Укажите данные для анализа
Укажите данные для анализа. Введите адрес ячейки для первой переменной в поле «Диапазон 1», выберите вторую переменную и укажите ее адрес ячейки в поле «Диапазон 2».
Шаг 5: Выберите уровень значимости
Выберите уровень значимости в соответствии с вашими потребностями. Обычный уровень значимости равен 0,05.
Шаг 6: Нажмите «ОК»
Нажмите кнопку «ОК», чтобы начать расчет ранговой корреляции Спирмена.
Шаг 7: Проверьте результаты
Результаты расчета ранговой корреляции Спирмена MS Excel будут выведены в новом листе Excel. Проверьте результаты и убедитесь, что они верны. Если что-то не так, повторите шаги 2-6.
Интерпретация результатов ранговой корреляции Спирмена в MS Excel
Ранговая корреляция Спирмена — это статистический метод, который используется для измерения связи между двумя переменными. Когда вы применяете этот метод в MS Excel, результатом будет коэффициент корреляции, который может иметь значение от -1 до 1.
Если коэффициент равен 1, это означает, что две переменные имеют положительную корреляцию, то есть, если одна переменная увеличивается, то и другая увеличивается. Если же коэффициент равен -1, то две переменные имеют отрицательную корреляцию, то есть, если одна переменная увеличивается, то другая уменьшается.
Коэффициент корреляции, близкий к 0, означает слабую связь между двумя переменными. Однако, нужно учитывать, что корреляция не всегда означает причинно-следственную связь между переменными, а лишь указывает на наличие связи между ними.
- Если коэффициент корреляции близок к 1 или -1, можно считать, что две переменные имеют сильную связь.
- Если коэффициент равен 0, то можно считать, что связь между переменными отсутствует.
- Если значение коэффициента корреляции находится между 0 и 1 (или 0 и -1), то можно говорить о наличии слабой связи между переменными.
Важно понимать, что интерпретация результатов ранговой корреляции Спирмена в MS Excel зависит от конкретной ситуации и контекста, в котором применяется этот метод. Поэтому, перед применением данного метода необходимо провести анализ данных и определить цель исследования.
Вопрос-ответ
Какая ранжировка используется при расчете ранговой корреляции Спирмена?
Ранжировка происходит по возрастанию значений переменных, после чего каждой из них присваивается порядковый номер по ранжировке. Если имеются повторяющиеся значения, то им присваивается средний порядковый номер. И уже на основе порядковых номеров вычисляется коэффициент корреляции.
Как выявить наличие корреляции между двумя переменными в Excel?
Для этого необходимо выбрать два столбца с переменными, затем на вкладке «Данные» выбрать «Анализ данных», в открывшемся меню выбрать «Корреляция», далее ввести диапазоны значений переменных. В появившемся окне выбрать «Ранговая корреляция Спирмена», после чего нажать ОК. В результате будет получено значение коэффициента корреляции Спирмена и его статистическая значимость.
Как интерпретировать полученное значение коэффициента ранговой корреляции Спирмена?
Значение коэффициента корреляции может быть в диапазоне от -1 до +1. Если коэффициент близок к +1, то переменные положительно коррелируют (при увеличении значений одной переменной увеличиваются и значения другой переменной), если близок к -1, то переменные отрицательно коррелируют (при увеличении значений одной переменной уменьшаются значения другой переменной). Если значение коэффициента близко к 0, то корреляции между переменными нет.
Можно ли использовать ранговую корреляцию Спирмена для большого количества переменных?
Ранговую корреляцию Спирмена можно использовать для любого числа переменных, однако при увеличении количества переменных сложность расчета и интерпретации результатов растет. В этом случае рекомендуется использовать другие методы многомерной статистики.
Как понять, что полученный коэффициент корреляции Спирмена статистически значим?
Для того, чтобы понять, что полученный коэффициент корреляции Спирмена статистически значим, необходимо сравнить его с критическим значением коэффициента при заданном уровне значимости и числе наблюдений. Если полученное значение коэффициента больше критического, то различия между переменными статистически значимы, если меньше — то нет.
17 авг. 2022 г.
читать 3 мин
В статистике корреляция относится к силе и направлению связи между двумя переменными. Значение коэффициента корреляции может варьироваться от -1 до 1 со следующими интерпретациями:
- -1: идеальная отрицательная связь между двумя переменными
- 0: нет связи между двумя переменными
- 1: идеальная положительная связь между двумя переменными
Один особый тип корреляции называется ранговой корреляцией Спирмена и используется для измерения корреляции между двумя ранжированными переменными. (например, оценка балла учащегося на экзамене по математике и оценка его оценки на экзамене по естественным наукам в классе).
В этом руководстве объясняется, как рассчитать ранговую корреляцию Спирмена между двумя переменными в Excel.
Пример: ранговая корреляция Спирмена в Excel
Выполните следующие шаги, чтобы вычислить ранговую корреляцию Спирмена между результатами экзамена по математике и результатами экзамена по естественным наукам 10 учащихся в определенном классе.
Шаг 1: Введите данные.
Введите экзаменационные баллы для каждого учащегося в два отдельных столбца:
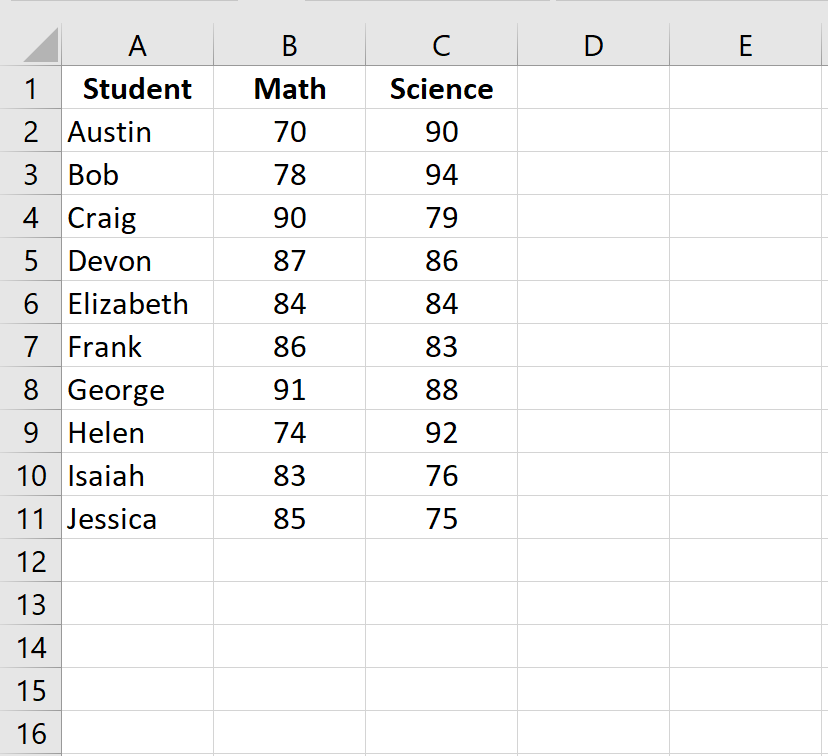
Шаг 2: Рассчитайте ранги для каждого экзаменационного балла.
Далее мы рассчитаем рейтинг для каждого экзаменационного балла. Используйте следующие формулы в ячейках D2 и E2, чтобы вычислить рейтинги по математике и естественным наукам для первого ученика, Остина:
Ячейка D2: =RANK.AVG(B2, $B$2:$B$11, 0)
Ячейка E2: =RANK.AVG(C2, $C$2:$C$11, 0)
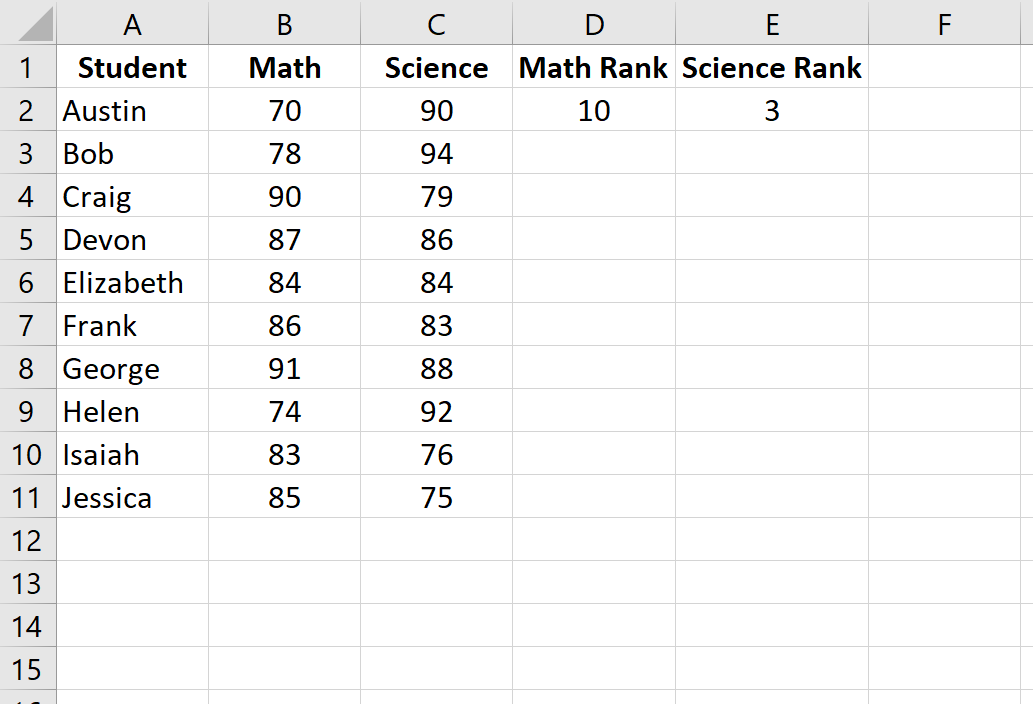
Затем выделите оставшиеся ячейки для заполнения:
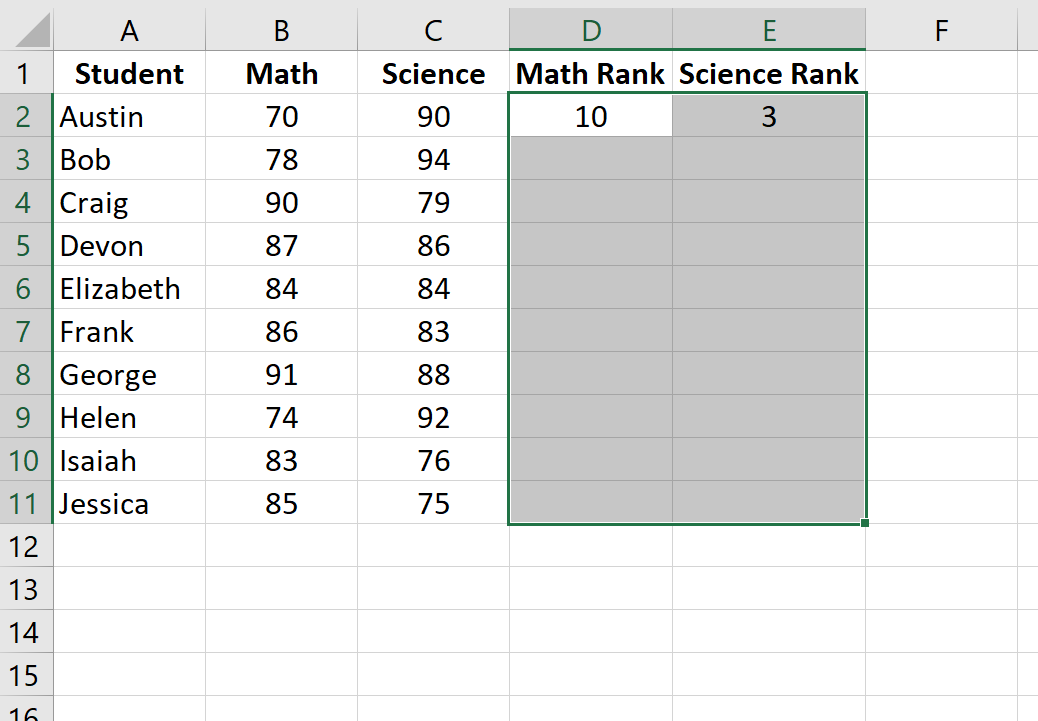
Затем нажмите Ctrl+D, чтобы заполнить ранги для каждого ученика:
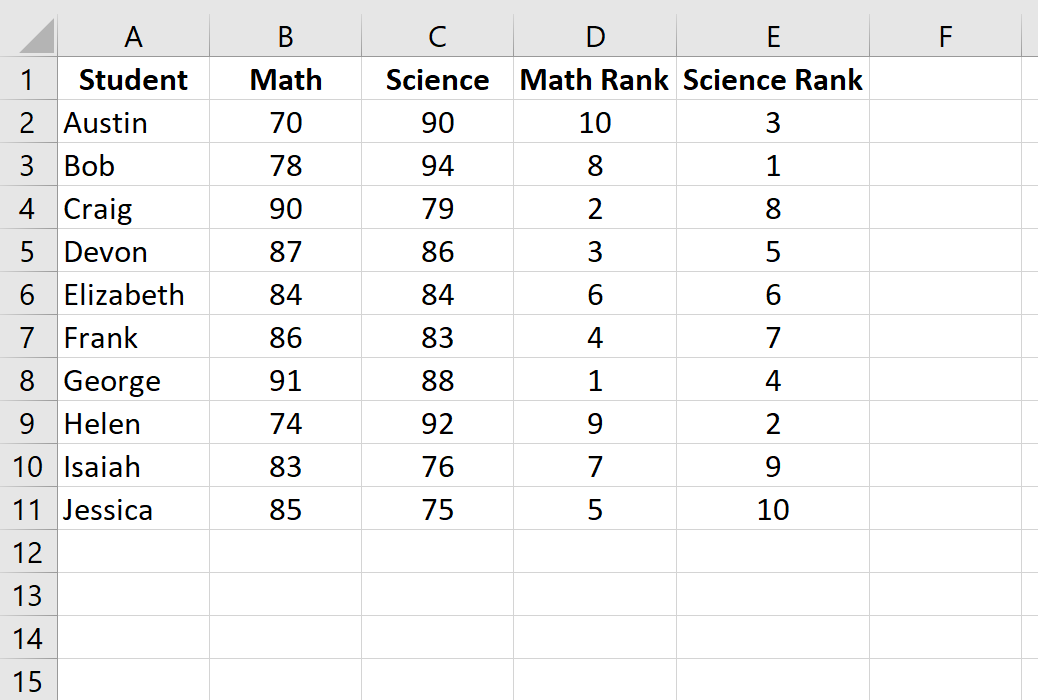
Шаг 3: Рассчитайте коэффициент ранговой корреляции Спирмена.
Наконец, мы рассчитаем коэффициент ранговой корреляции Спирмена между оценками по математике и по естественным наукам с помощью функции CORREL() :
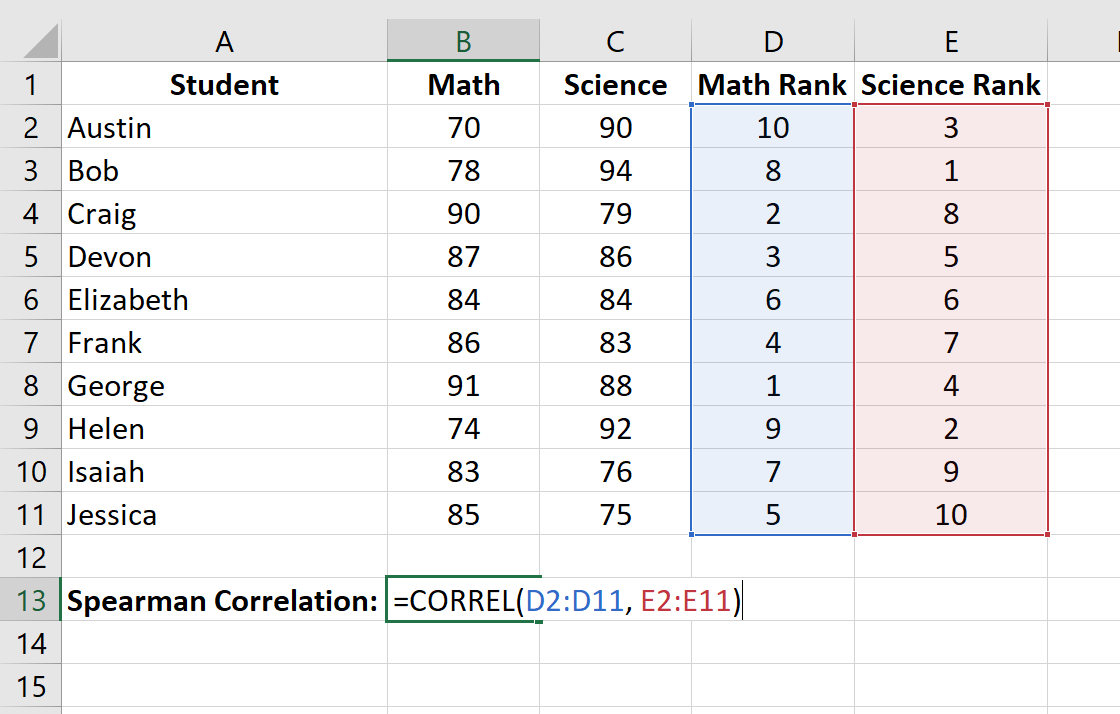
Ранговая корреляция Спирмена оказывается равной -0,41818 .
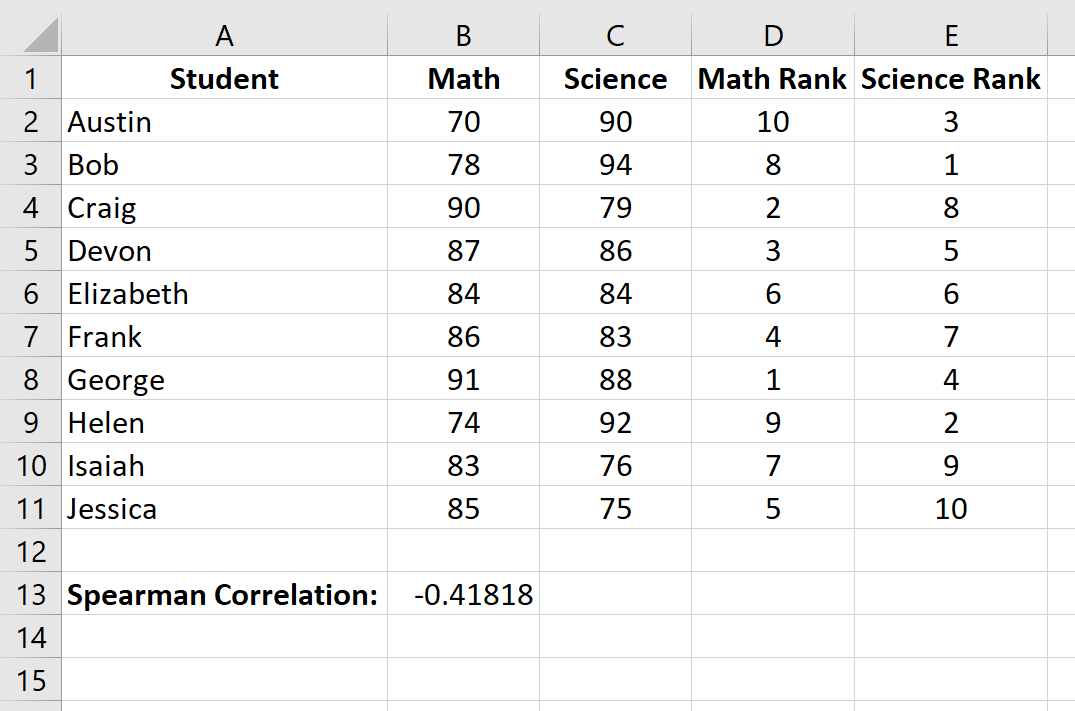
Шаг 4 (необязательно): Определите, является ли ранговая корреляция Спирмена статистически значимой.
На предыдущем шаге мы обнаружили, что ранговая корреляция Спирмена между результатами экзаменов по математике и естественным наукам составляет -0,41818 , что указывает на отрицательную корреляцию между двумя переменными.
Однако, чтобы определить, является ли эта корреляция статистически значимой, нам нужно будет обратиться к таблице ранговой корреляции Спирмена критических значений, которая показывает критические значения, связанные с различными размерами выборки (n) и уровнями значимости (α).
Если абсолютное значение нашего коэффициента корреляции больше критического значения в таблице, то корреляция между двумя переменными является статистически значимой.
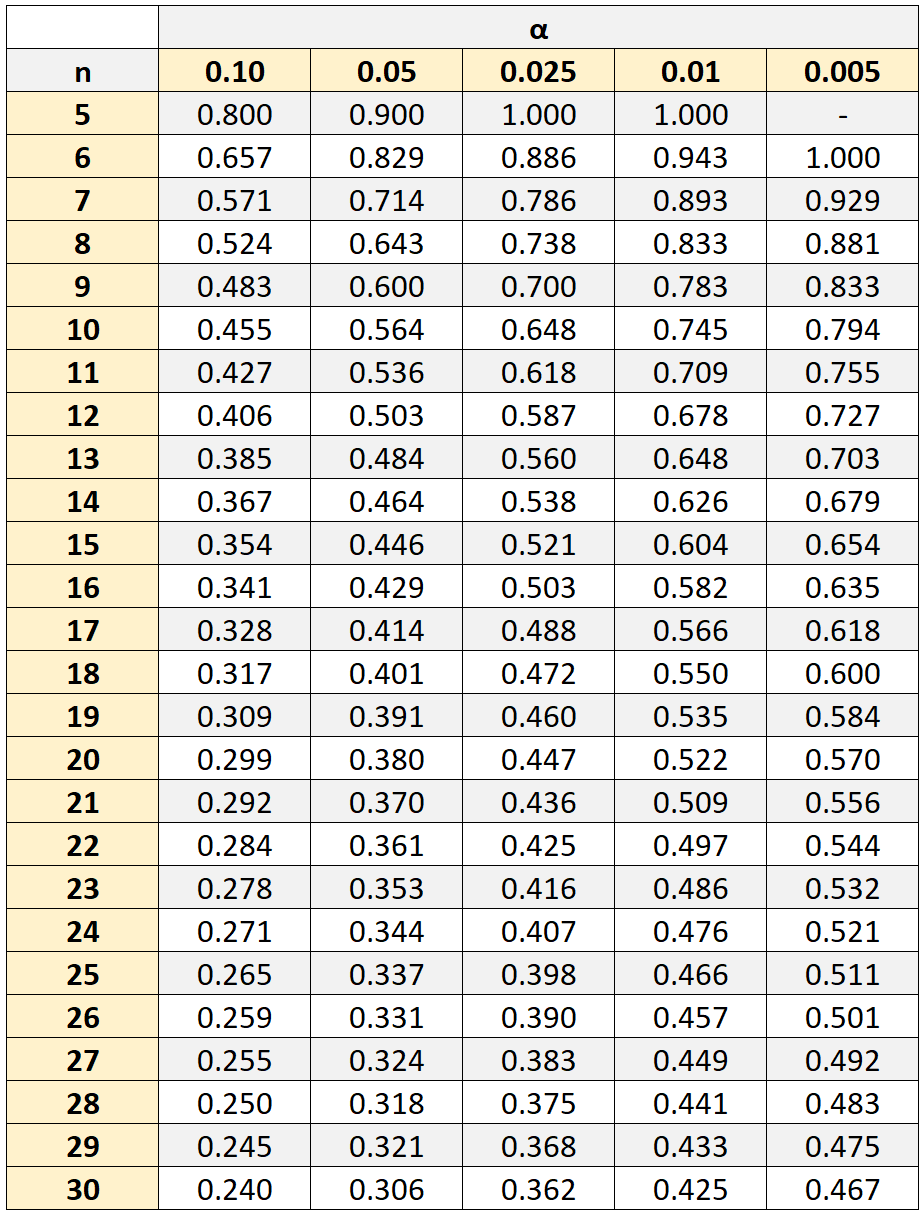
В нашем примере размер выборки составлял n = 10 студентов. Используя уровень значимости 0,05, мы находим, что критическое значение равно 0,564 .
Поскольку рассчитанное нами абсолютное значение рангового коэффициента корреляции Спирмена ( 0,41818 ) не превышает этого критического значения, это означает, что корреляция между баллами по математике и естественным наукам не является статистически значимой.
Загрузить PDF
Загрузить PDF
Коэффициент корреляции ранга Спирмена позволяет определить, существует ли между двумя переменными зависимость, выражаемая монотонной функцией (то есть при росте одной переменной увеличивается и вторая, и наоборот). Приведенные в статье простые шаги позволят вам производить расчеты вручную, а также вычислять коэффициент корреляции при помощи программ Excel и R.
-

1
Составьте таблицу данных. Таким образом вы упорядочите информацию, необходимую для расчета коэффициента корреляции ранга Спирмена. При этом вам понадобится:
- 6 колонок, озаглавленных так, как показано выше на рисунке.
- Количество строк, соответствующее числу пар переменных.
-

2
Заполните первые две колонки парами переменных.
-

3
В третьей колонке запишите номера (ранги) пар переменных от 1 до n (общее число пар). Присвойте номер 1 паре с наименьшим значением в первой колонке, 2 — следующему за ним значению, и так по возрастанию величин переменной из первой колонки.
-

4
В четвертой колонке сделайте то же, что и в третьей, но на этот раз пронумеруйте пары переменных по второй колонке таблицы.
-

Если два (или более) значения переменной в одной колонке одинаковы, расположите их один за другим и найдите среднее значение их номеров, затем пронумеруйте их этим средним значением.
В приведенном справа примере два значения переменной совпадают и равны 5; в случае нормальной нумерации эти данные получили бы ранги 2 и 3. Поскольку значения одинаковы, находим среднюю величину их рангов. Среднее 2 и 3 равно 2,5, поэтому обеим величинам присваиваем ранг 2,5.
-
-

5
В колонке «d» вычислите разность между двумя рангами из предыдущих двух колонок. Например, если ранг в третьей колонке равен 1, а в четвертой – 3, то разница между ними составит 2. Знак не имеет значения, поскольку на следующем шаге эти числа будут возведены в квадрат.
-

6
Возведите каждое значение из колонки «d» в квадрат и запишите полученные величины в колонку «d2«.
-
7
Просуммируйте все значения из колонки «d2«. Вы определите сумму Σd2.

-
8
Воспользуйтесь одной из следующих формул:
-
9
Проанализируйте результат. Полученное значение находится между -1 и 1.
- Если оно близко к -1, корреляция отрицательна.
- Если близко к 0, корреляция отсутствует.
- Если близко к 1, наблюдается положительная корреляция.
- Не забудьте поделить на сумму переменных и взять корень. После этого поделите на Σd2.

Реклама
-
1
Создайте новые колонки с рангами, соответствующими колонкам данных. Например, если данные внесены в Колонку A2:A11, используйте функцию «=RANK(A2,A$2:A$11)» и занесите результаты для всех строк в новую колонку.
-
2
Найдите ранги для одинаковых величин, как описано в шагах 3 и 4 метода 1.
-
3
В новой ячейке определите корреляцию между двумя колонками рангов с помощью функции «=CORREL(C2:C11,D2:D11)». В данном случае C и D – это колонки, содержащие ранги. Таким образом, в данной ячейке вы получите коэффициент ранговой корреляции Спирмена.
Реклама
-
1
Если у вас еще нет программы R для обработки статистических данных, приобретите ее (см. http://www.r-project.org).
-
2
Сохраните данные в формате CSV, расположив их в двух колонках, корреляцию между которыми вы собираетесь исследовать. Сохранить файл в данном формате легко посредством опции «Сохранить как».
-
3
Откройте редактор R. Если вы еще не вошли в программу R, просто запустите ее. Для этого достаточно нажать иконку R на рабочем столе.
-
4
Наберите команды:
- d <- read.csv(«NAME_OF_YOUR_CSV.csv») и нажмите клавишу ввода
- cor(rank(d[,1]),rank(d[,2]))
Реклама
Советы
- Как правило, набор данных должен состоять не менее чем из 5 пар для того, чтобы можно было достоверно установить какую-либо корреляцию (3 пары было использовано в примере выше для простоты).
Реклама
Предупреждения
- Коэффициент ранговой корреляции Спирмена позволяет установить лишь то, растут ли обе переменные или уменьшаются одновременно. Если разброс данных слишком велик, этот коэффициент не даст точного значения корреляции.
- Приведенная функция даст верный результат при отсутствии одинаковых значений в массиве данных. Если такие значения существуют, как в рассмотренном нами примере, необходимо использовать следующее определение: коэффициент корреляции, основанный на рангах.
Реклама
Об этой статье
Эту страницу просматривали 70 067 раз.
Была ли эта статья полезной?
Приложения
3. Ранговая корреляция по Спирмену
В тех случаях, когда необходимо установить возможную функциональную связь между двумя изучаемыми параметрами, используют метод называемый ранговой корреляцией. Например, группа испытуемых последовательно выполняет тестовые задания в беге на 30м и тройном прыжке с места. Требуется определить влияет ли уровень развития быстроты на результат в прыжке.
В поисках ответа на поставленный вопрос сравнивают места (ранги), которые занимает каждый участник в каждом из обоих видов.
Иногда даже визуальное сопоставление рангов говорит в пользу функциональной взаимозависимости исследуемых показателей. Однако более обоснованное заключение можно получить лишь с помощью приемов статистической обработки материала. Ее технологии достаточно проста и она изложена в табл. 4
Таблица 4
Определение коррелятивной зависимости между результатами в беге на 30м и тройным прыжком с места
|
№ пп |
Испытуемые (n = 10) |
Тройной с места (см) |
Ранги |
Бег 30 м (с) |
Ранги |
Разность рангов di |
Квадраты разности рангов di2 |
|
1 |
А. |
744 |
5 |
4,2 |
5,5 |
0,5 |
0,25 |
|
2 |
Б |
613 |
10 |
4,5 |
10 |
0 |
0 |
|
3 |
В |
737 |
6,5 |
4,3 |
7,5 |
1 |
1 |
|
4 |
Г |
623 |
8 |
4,3 |
7,5 |
1,5 |
2,25 |
|
5 |
Д |
618 |
9 |
4,4 |
9 |
0 |
0 |
|
6 |
Е |
745 |
3,5 |
4,0 |
2,5 |
1 |
1 |
|
7 |
Ж |
737 |
6,5 |
4,2 |
5,5 |
1 |
1 |
|
8 |
З |
750 |
2 |
4,0 |
2,5 |
1,5 |
2,25 |
|
9 |
И |
745 |
3,5 |
4,1 |
4 |
0,5 |
0,25 |
|
10 |
К |
760 |
1 |
3,9 |
1 |
0 |
0 |
Сначала в таблицу вносятся результаты испытуемых в тройном прыжке и определяются ранги (места) каждого участника. Если два или более результата одинаковы, то им присваивается одинаковый ранг, составляющий среднеарифметическое значение нормального ряда чисел (см. § 2). Далее в очередную графу вносятся результаты в беге, которые ранжируются по уже известной схеме.
Сопоставляя парные ранги, находят их арифметическую разность (di), после чего каждая из найденных разностей возводится в квадрат (di2). Затем определяется сумма этих квадратов разностей (∑di2). Далее с помощью формулы находится коэффициент корреляции, (число 6 в формуле – постоянное).
Сумма квадратов разностей в нашем случае составила 4,0. Подставляя все значения в формулу, находим, что r = 0,98
Из таблицы 5 находим, что при n = 10 значимый уровень корреляции составляет менее 0,001, что говорит об очень высокой функциональной взаимосвязи исследуемых показателей.
Таблица 5
Минимальные значения коэффициентов нормальной корреляции, при которых связь между двумя рядами наблюдений можно считать значимой с уровнем надежности Р; n – число пар сравниваемых наблюдений
|
Р n |
0,05 |
0,01 |
0,005 |
|
5 |
0,669 |
0,833 |
0,875 |
|
7 |
0,582 |
0,750 |
0,798 |
|
10 |
0,497 |
0,658 |
0,708 |
|
12 |
0,457 |
0,612 |
0,661 |
|
15 |
0,412 |
0,558 |
0,606 |
|
18 |
0,378 |
0,516 |
0,561 |
|
20 |
0,360 |
0,492 |
0,537 |
|
25 |
0,323 |
0,445 |
0,487 |
|
30 |
0,296 |
0,409 |
0,449 |
В табличном редакторе Excel коэффициент корреляции находим, вычислив ранги, как было показано выше.

Рис. 4. Вставка формулы в «строку формул»
Затем в следующем столбце (К) найдем разности рангов с последующим возведением в квадрат (столбец L), для чего в «строку формул» внесем нужные формулы: =H3-J3 и = Кˆ2. В ячейке L14 находим сумму квадратов разностей рангов (СУММ (L3:L12)) (рис. 4).
Далее на основании полученных цифровых данных производим расчет коэффициента корреляции. Для этого в «строку формул» вносим формулу =1-(6*L14)/(10*(10ˆ2-1)) (рис. 5).
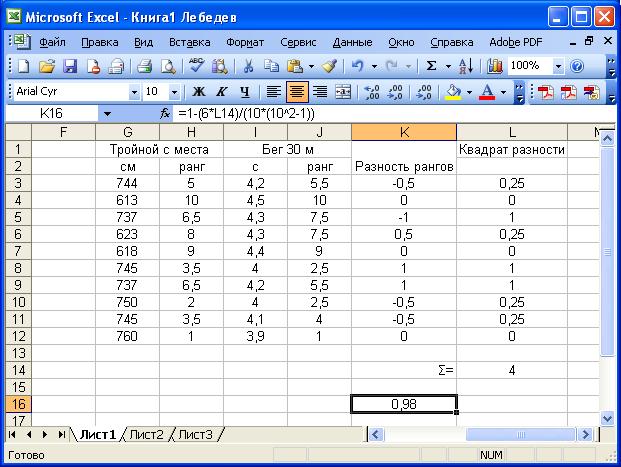
Рис. 4. Вставка формулы в «строку формул»
Затем в следующем столбце (К) найдем разности рангов с последующим возведением в квадрат (столбец L), для чего в «строку формул» внесем нужные формулы: =H3-J3 и = Кˆ2. В ячейке L14 находим сумму квадратов разностей рангов (СУММ (L3:L12)) (рис. 4).
Далее на основании полученных цифровых данных производим расчет коэффициента корреляции. Для этого в «строку формул» вносим формулу =1-(6*L14)/(10*(10ˆ2-1)) (рис. 5).

Рис. 5. Расчет коэффициента корреляции
Кроме рассмотренных непараметрических существуют параметрические методы математической статистики. К ним относятся критерий Т Крамера – Уэлча, t-критерий Стьюдента, корреляция Пирсона. Они более точны, хотя и более трудоемки, однако сфера их применения ограничена выборками с относительно небольшими отклонениями параметров от их средней величины.
Таким образом, достоверность сдвигов с применением этих методик может определяться как в «ручном» варианте, так и с помощью специальных компьютерных программ.

