Содержание
- Этапы решения задач с использованием компьютера
- Учитель информатики
- Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
- § 2.1. Решение задач на компьютере
- Этапы решения задачи на компьютере
- Задача о пути торможения автомобиля
- Вопросы и задания к § 2.1. Решение задач на компьютере
- Решение задач на компьютере. Этапы решения задачи на компьютере
- Урок 12. Информатика 9 класс ФГОС
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Решение задач на компьютере. Этапы решения задачи на компьютере»
- Глава 8. Технология подготовки и решения задач с помощью компьютера
- 8.1. Какие этапы включает в себя решение задач с помощью компьютера?
- 8.2. Что называют математической моделью?
- 8.3. Какие основные этапы содержит процесс разработки программ?
- 8.4. Как проконтролировать текст программы до выхода на компьютер?
- 8.5. Для чего нужны отладка и тестирование?
- 8.6. В чем заключается отладка?
- 8.7. Что такое тест и тестирование?
- 8.8. Какими должны быть тестовые данные?
- 8.9. Из каких этапов состоит процесс тестирования?
- 8.10. Каковы характерные ошибки программирования?
- 8.11. Является ли отсутствие синтаксических ошибок свидетельством правильности программы?
- 8.12. Какие ошибки не обнаруживаются транслятором?
- 8.13. В чем заключается сопровождение программы?
- 8.14. Вопросы для самоконтроля
- 8.15. Упражнения
Этапы решения задач с использованием компьютера



Рассмотрим эти этапы на следующем примере: пусть требуется вычислить сумму двух целых чисел и вывести на экран видеомонитора результат.
Первый этап – постановка задачи. На этом этапе участвует человек, хорошо представляющий предметную область задачи. Он должен четко определить цель задачи, дать словесное описание содержания задачи и предложить подход к ее решению. Для задачи вычисления суммы двух целых чисел человек, знающий, как складываются числа, может описать задачу следующим образом: ввести два целых числа, сложить их и вывести сумму в качестве результата решения задачи.
Второй этап – математическое или информационное моделирование. Цель этого этапа – создать такую математическую модель решаемой задачи, которая может быть реализована в компьютере. Существует целый ряд задач, где математическая постановка сводится к простому перечислению формул и логических условий. Этот этап тесно связан с первым этапом, и его можно отдельно не рассматривать, однако возможно, что для полученной модели известны несколько методов решения, и тогда предстоит выбрать лучший. Для вышеописанной задачи данный этап сводится к следующему: введенные в компьютер числа запомним в памяти под именами А и В, затем вычислим значение суммы этих чисел по формуле А+В, и результат запомним в памяти под именем Summa.
Третий этап – алгоритмизация задачи. На основе математического описания необходимо разработать алгоритм решения.
Алгоритмом называется точное предписание, определяющее последовательность действий исполнителя, направленных на решение поставленной задачи. В роли исполнителей алгоритмов могут выступать люди, роботы, компьютеры.
Используются различные способы записи алгоритмов. Широко распространен словесный способ записи: это записи рецептов приготовления различных блюд в кулинарной книге, инструкции по использованию технических устройств, правила правописания и многие другие. Наглядно представляется алгоритм языком блок-схем.
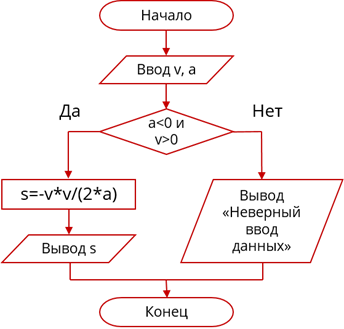
Например, алгоритм решения задачи вычисления суммы двух целых чисел на языке блок-схем будет записан, как показано на рис. 1.
Свойства алгоритма. При составлении и записи алгоритма необходимо обеспечить, чтобы он обладал рядом свойств.
Однозначность алгоритма, под которой понимается единственность толкования исполнителем правил выполнения действий и порядка их выполнения. Чтобы алгоритм обладал этим свойством, он должен быть записан командами из системы команд исполнителя.
Для нашего примера исполнитель алгоритма должен понимать такую запись действий, как сложить числа А и В.
Конечность алгоритма – обязательность завершения каждого из действий, составляющих алгоритм, и завершаемость выполнения алгоритма в целом. Записанный на рис.1 алгоритм обладает этим свойством, так как запись действий исполнителя завершается записью об окончании алгоритма.
Результативность алгоритма, предполагающая, что выполнение алгоритма должно завершиться получением определенных результатов. Алгоритм в нашем примере обладает этим свойством, так как для целых чисел А и В всегда будет вычислена сумма.
Массовость, т.е. возможность применения данного алгоритма для решения целого класса задачи. Так как алгоритм, показанный на рис.1, позволяет правильно подсчитать сумму не только чисел 2 и 3, но любой другой пары целых чисел, он обладает свойством массовости. Для того чтобы алгоритм обладал свойством массовости, следует составлять алгоритм, используя обозначения величин и избегая конкретных значений.
Правильность алгоритма, под которой понимается способность алгоритма давать правильные результаты решения поставленных задач. Представленный в примере алгоритм обладает свойством правильности, так как в нем использована правильная форма сложения целых чисел, и для любой пары целых чисел результат выполнения алгоритма будет равен их сумме.

Четвертый этап – программирование. Программой называется план действий, подлежащих выполнению некоторым исполнителем, в качестве которого может выступать компьютер. Составление программы обеспечивает возможность выполнения алгоритма и соответственно поставленной задачи исполнителем-компьютером. Во многих задачах при программировании на алгоритмическом языке часто пользуются заменой блока алгоритма на один или несколько операторов, введением новых блоков, заменой одних блоков другими.
Пятый этап – ввод программы и исходных данных в ЭВМ. Программа и исходные данные вводятся в ЭВМ с клавиатуры с помощью редактора текстов, и для постоянного хранения осуществляется их запись на гибкий или жесткий магнитный диск.
Шестой этап – тестирование и отладка программы. На этом этапе происходят исполнение алгоритма с помощью ЭВМ, поиск и исключение ошибок. При этом программисту приходится выполнять рутинную работу по проверке работы программы, поиску и исключению ошибок, и поэтому для сложных программ этот этап часто требует гораздо больше времени и сил, чем написание первоначального текста программы.
Отладка программы – сложный и нестандартный процесс. Исходный план отладки заключается в том, чтобы оттестировать программу на контрольных примерах.
Контрольные примеры стремятся выбрать так, чтобы при работе с ними программа прошла все основные пути блок-схемы алгоритма, поскольку на каждом из путей могут быть свои ошибки, а детализация плана зависит от того, как поведет себя программа на этих примерах: на одном она может зациклится (т.е. бесконечно повторять одно и то же действие); на другом – дать явно неверный или бессмысленный результат и т.д. Сложные программы отлаживают отдельными фрагментами.
Для повышения качества выполнения этого этапа используются специальные программы – отладчики, которые позволяют исполнить программу «по шагам» с наблюдением за изменением значений переменных, выражений и других объектов программы, с отслеживанием выполняемых операторов.
Седьмой этап – исполнение отлаженной программы и анализ результатов. На этом этапе программист запускает программу и задает исходные данные, требуемые по условию задачи.
Полученные в результате решения выходные данные анализируются постановщиком задачи, и на основании этого анализа вырабатываются соответствующие решения, рекомендации, выводы. Например, если при решении задачи на компьютере результат сложения двух чисел 2 и 3 будет 4, то следует сделать вывод о том, что надо изменить алгоритм и программу.
Возможно, что по итогам анализа результатов потребуются пересмотр самого подхода к решению задачи и возврат к первому этапу для повторного выполнения всех этапов с учетом приобретенного опыта. Таким образом, в процессе создания программы некоторые этапы будут повторяться до тех пор, пока мы получим алгоритм и программу, удовлетворяющие показанным выше свойствам.
Источник
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 2.1. Решение задач на компьютере
Информатика. 9 класса. Босова Л.Л. Оглавление
Ключевые слова:
Этапы решения задачи на компьютере
Чтобы решать задачи на компьютере, необходимо владеть языком программирования, обладать знаниями в области информационного моделирования и алгоритмизации.
Решение задачи с использованием компьютера включает в себя этапы, показанные на рис. 2.1.
На первом этапе обычно осуществляется постановка задачи, происходит осознание её условия. При этом должно быть чётко определено, что дано (какие исходные данные известны, какие данные допустимы) и что требуется найти в решаемой задаче. Также должны быть чётко выделены существенные свойства рассматриваемого объекта, указаны связи между исходными данными и результатами.
На втором этапе описательная информационная модель формализуется, т. е. записывается с помощью некоторого формального языка.

Для этого требуется:
На третьем этапе осуществляется построение алгоритма — чёткой инструкции, задающей необходимую последовательность действий для решения задачи. Алгоритм чаще всего представляется в форме блок-схемы ввиду её наглядности и универсальности.
На четвёртом этапе алгоритм записывается на одном из языков программирования. Вы учитесь записывать программы на языке Паскаль.
На пятом этапе осуществляется отладка и тестирование программы. Этап отладки и тестирования также называют компьютерным экспериментом.
Отладка программы — это процесс проверки работоспособности программы и исправления обнаруженных при этом ошибок. Ошибки могут быть связаны с нарушением правил записи программы на конкретном языке программирования. Их программисту помогает найти используемая система программирования; она выдаёт на экран сообщения о выявленных ошибках.
Проверка правильности разработанной программы осуществляется с помощью тестов. Тест — это конкретный вариант значений исходных данных, для которого известен ожидаемый результат.
О правильности разработанной программы свидетельствует также соответствие полученных данных экспериментальным фактам, теоретическим положениям и т. д. При этом может возникнуть необходимость уточнить разработанную математическую модель, полнее учесть особенности изучаемого объекта или процесса. По уточнённой математической модели снова составляется программа, анализируются результаты её выполнения. Так продолжается до тех пор, пока полученные результаты не будут достаточно точно соответствовать изучаемому объекту.
Задача о пути торможения автомобиля
Рассмотрим последовательность прохождения этапов решения задачи на компьютере (см. рис. 2.1) на примере простой задачи.
Водитель автомобиля, движущегося с некоторой постоянной скоростью, увидев красный свет светофора, нажал на тормоз. После этого скорость автомобиля стала уменьшаться каждую секунду на 5 метров. Требуется найти расстояние, которое автомобиль пройдёт до полной остановки.
Первый этап.
Требуется найти: sx — расстояние, которое автомобиль пройдёт до полной остановки.
Второй этап. В данной ситуации мы имеем дело с прямолинейным равноускоренным движением тела. Формула для перемещения при этом имеет вид:

Упростим эту формулу с учётом того, что конечная скорость равна нулю:


Третий этап. Представим алгоритм решения задачи в виде блок-схемы:

Четвёртый этап. Запишем данный алгоритм на языке программирования Паскаль:
Пятый этап. Протестировать составленную программу можно, используя информацию, что при скорости 72 км/ч с начала торможения до полной остановки автомобиль проходит 40 метров.
Выполнив программу несколько раз при различных исходных данных, можно сделать вывод: чем больше начальная скорость автомобиля, тем большее расстояние он пройдёт с начала торможения до полной остановки.
Применяя компьютер для решения задач, всегда следует помнить, что наряду с огромным быстродействием и абсолютной исполнительностью у компьютера отсутствуют интуиция и чувство здравого смысла, и он способен решать только ту задачу, программу решения которой ему подготовил человек.
САМОЕ ГЛАВНОЕ
Этапы решения задачи с использованием компьютера:1) постановка задачи;
2) формализация;
3) алгоритмизация;
4) программирование;
5) компьютерный эксперимент.Для решения задач на компьютере необходимо владеть языком программирования, обладать знаниями в области информационного моделирования и алгоритмизации.
Вопросы и задания к § 2.1. Решение задач на компьютере
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Какими слайдами вы могли бы дополнить презентацию?
Источник
Решение задач на компьютере. Этапы решения задачи на компьютере
Урок 12. Информатика 9 класс ФГОС


В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности



Конспект урока «Решение задач на компьютере. Этапы решения задачи на компьютере»
Вы уже знаете, что компьютер был создан для решения задач и обработки данных. И наверняка задавались вполне логичным вопросом: «А как именно решить ту или иную задачу с помощью компьютера?».
Решение любой задачи с помощью компьютера можно разделить на пять основных этапов:
1. Постановка задачи.
2. Формализация задачи.
3. Создание алгоритма.
5. Тестирование и отладка.
Постановка задачи. На этапе постановки задачи нужно понять условие задачи, выделить исходные и результирующие данные и понять отношения между ними. Проще говоря, нужно ответить на вопросы:
· «Что нужно найти по условию задачи?»
· «Чем можно пользоваться при решении задачи?»
Формализация задачи. Во время этого этапа нужно записать описательную информационную модель, созданную на этапе постановки задачи, каким-либо формальным языком, например математическими формулами, и адаптировать эти формулы для решения данной задачи. То есть нам нужно записать при помощи формул соотношения между данными задачи и понять, при помощи каких формул можно найти результирующие данные из исходных. Иначе говоря, создать математическую модель, описывающую явление или объект, которые фигурируют в условии.
Как ясно из названия следующего этапа «Создание алгоритма», его результатом должен быть алгоритм или конкретная последовательность действий. Алгоритм создаётся на основании математической модели.
При создании алгоритма должны быть соблюдены два условия:
· Созданный алгоритм должен быть конкретной последовательностью действий, которая приводит к получению результирующих данных из исходных.
· Созданный алгоритм должен быть понятен человеку, который будет писать по нему программу.
Чаще всего алгоритм записывается в форме блок-схемы, потому что данная форма записи достаточно наглядна и универсальна.
Пример блок-схемы
На этапе программирования алгоритм записывается с помощью какого-нибудь языка программирования. То есть результатом работы на данном этапе должна быть программа. Мы будем писать программы на языке Pascal.

Пример программы на языке Pascal
На этапе тестирования и отладки проверяется, работает ли программа, если работает, то правильно ли. Проверяется отсутствие ошибок в программе. Ошибки делятся на синтаксические, которые связаны с нарушением правил записи программы на конкретном языке программирования, и логические, которые могут быть связаны с недостаточно точной математической моделью, недостаточно точным алгоритмом или же неточной записью алгоритма на языке программирования. Синтаксические ошибки находятся при помощи программных средств, а логические ошибки находятся с помощью тестов.
Тест – это набор конкретных значений исходных данных, при которых известен ожидаемый результат работы программы.
Если результаты работы программы соответствуют ожидаемым – значит задача решена, иначе – на одном из этапов допущена логическая ошибка. Например недостаточно точно сформулирована математическая модель. А так как все этапы связаны между собой – это повлекло неточности при создании алгоритма и программировании. Чтобы исправить ошибку возвращаются к этапу формализации задачи и уточняют математическую модель, после чего вносят правки в алгоритм и программу. Далее программа снова отлаживается и тестируется. Так происходит до тех пор, пока программа не будет соответствовать всем требованиям.
Обратим внимание на то, что этапы постановки и формализации задачи могут требовать наличия некоторых знаний из предметной области задачи. Например, если наша задача из области авиастроения – то без знаний из этой области мы не сможем узнать отношений между исходными и результирующими данными, а тем более записать их в виде формул.
Этапы создания алгоритма и программирования требуют наличия знаний по программированию. Так как на третьем этапе определяется каким образом будет решаться та или иная подзадача. А от этого зависит скорость работы программы, и количество потребляемых ею ресурсов системы, например оперативной памяти. На четвёртом этапе записать алгоритм тоже можно различными способами.
На этапе тестирования и отладки требуются как знания по предметной области, так и некоторое знание основ программирования. Так как без знаний в предметной области мы не можем знать результирующих данных в тестах, а без знаний в программировании мы не сможем отыскать ошибки и составить наиболее полный набор тестов, учитывающий все частные случаи и исключения.
Таким образом, решение задачи с помощью компьютера можно изобразить в виде схемы. На этапе постановки задачи ставиться её условие, а результатом работы на данном этапе будут исходные и результирующие данные, которые, в свою очередь, поступают на этап «Формализации задачи». На данном этапе составляется математическая модель, по ней составляют алгоритм, который записывают в одной из форм. По алгоритму составляется программа, которая отлаживается и тестируется. Если программа работает неправильно, процесс решения возвращается к одному из предыдущих этапов, а если правильно – задача решена.
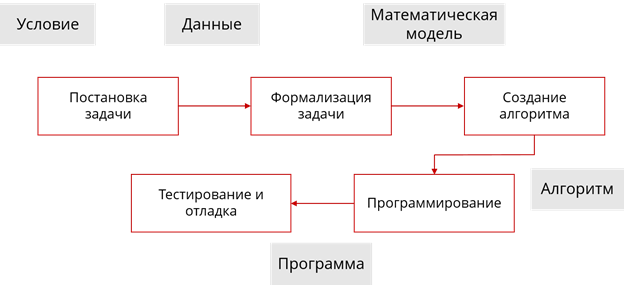
Схема решения задачи с помощью компьютера
Решение задач с помощью компьютера включает в себя:
1. Постановку задачи.
2. Формализацию задачи.
3. Создание алгоритма.
5. Тестирование и отладку.
Все этапы решения задачи связаны между собой.
Источник
Глава 8. Технология подготовки и решения задач с помощью компьютера
8.1. Какие этапы включает в себя решение задач с помощью компьютера?
8.2. Что называют математической моделью?
Математическая модель это система математических соотношений формул,
уравнений, неравенств и т.д., отражающих существенные свойства объекта или явления.
Позвольте, может сказать «заказчик», меня не устраивает такое упрощение. Я хочу знать точно, сколько времени будет падать камень в реальных условиях, а не в несуществующей пустоте.
Хорошо, согласится математик. Будем считать, что камень имеет сферическую форму и диаметр. Какого примерно он диаметра?
Около пяти сантиметров. Но он вовсе не сферический, а продолговатый.
Если тот, кто поставил задачу на «человеческом» языке не будет дальше вмешиваться в ход мысли математика, то последний через некоторое время даст численный ответ. Но «потребитель» может возражать по-прежнему: камень на самом деле вовсе не эллипсоидальный, давление воздуха в том месте и в тот момент не было равно 760 мм ртутного столба и т.д. Что же ответит ему математик?
Чтобы описать явление, необходимо выявить самые существенные его свойства, закономерности, внутренние связи, роль отдельных характеристик явления. Выделив наиболее важные факторы, можно пренебречь менее существенными.
Конечно, результаты вычислительного эксперимента могут оказаться и не соответствующими действительности, если в модели не будут учтены какие-то важные стороны действительности.
При построении математических моделей далеко не всегда удается найти формулы, явно выражающие искомые величины через данные. В таких случаях используются математические методы, позволяющие дать ответы той или иной степени точности.
Существует не только математическое моделирование какого-либо явления, но и визуально-натурное моделирование, которое обеспечивается за счет отображения этих явлений средствами машинной графики, т.е. перед исследователем демонстрируется своеобразный «компьютерный мультфильм», снимаемый в реальном масштабе времени. Наглядность здесь очень высока.
8.3. Какие основные этапы содержит процесс разработки программ?
Процесс разработки программы можно выразить следующей формулой:
На начальном этапе работы анализируются и формулируются требования к программе, разрабатывается точное описание того, что должна делать программа и каких результатов необходимо достичь с ее помощью.
Затем программа разрабатывается с использованием той или иной технологии программирования (например, структурного программирования).
Полученный вариант программы подвергается систематическому тестированию ведь наличие ошибок в только что разработанной программе это вполне нормальное закономерное явление. Практически невозможно составить реальную (достаточно сложную) программу без ошибок. Нельзя делать вывод, что программа правильна, лишь на том основании, что она не отвергнута машиной и выдала результаты. Все, что достигнуто в этом случае, это получение каких-то результатов, не обязательно правильных. В программе при этом может оставаться большое количество логических ошибок. Ответственные участки программы проверяются с использованием методов доказательства правильности программ.
Для каждой программы обязательно проводятся работы по обеспечению качества и эффективности программного обеспечения, анализируются и улучшаются временные характеристики.
8.4. Как проконтролировать текст программы до выхода на компьютер?
8.5. Для чего нужны отладка и тестирование?
Отладка программы это процесс поиска и устранения ошибок в программе, производимый по результатам её прогона на компьютере.
Тестирование (англ. test испытание) это испытание, проверка правильности работы программы в целом, либо её составных частей.
Тестирование устанавливает факт наличия ошибок, а отладка выясняет ее причину.
Английский термин debugging (» отладка «) буквально означает » вылавливание жучков «. Термин появился в 1945 г., когда один из первых компьютеров «Марк-1» прекратил работу из-за того, что в его электрические цепи попал мотылек и заблокировал своими останками одно из тысяч реле машины.
8.6. В чем заключается отладка?
8.7. Что такое тест и тестирование?
Как бы ни была тщательно отлажена программа, решающим этапом, устанавливающим ее пригодность для работы, является контроль программы по результатам ее выполнения на системе тестов.
Программу условно можно считать правильной, если её запуск для выбранной системы
тестовых исходных данных во всех случаях дает правильные результаты.
Для реализации метода тестов должны быть изготовлены или заранее известны эталонные результаты.
8.8. Какими должны быть тестовые данные?
8.9. Из каких этапов состоит процесс тестирования?
1. Проверка в нормальных условиях. Предполагает тестирование на основе данных, которые характерны для реальных условий функционирования программы.
2. Проверка в экстремальных условиях. Тестовые данные включают граничные значения области изменения входных переменных, которые должны восприниматься программой как правильные данные. Типичными примерами таких значений являются очень маленькие или очень большие числа и отсутствие данных. Еще один тип экстремальных условий это граничные объемы данных, когда массивы состоят из слишком малого или слишком большого числа элементов.
Наихудшая ситуация складывается тогда, когда программа воспринимает неверные данные как правильные и выдает неверный, но правдоподобный результат.
Программа должна сама отвергать любые данные, которые она не в состоянии обрaбатывать правильно.
8.10. Каковы характерные ошибки программирования?
Ошибки могут быть допущены на всех этапах решения задачи от ее постановки до оформления. Разновидности ошибок и соответствующие примеры приведены в таблице:
| Вид ошибки | Пример |
|---|---|
| Неправильная постановка задачи | Правильное решение неверно сформулированной задачи |
| Неверный алгоритм | Выбор алгоритма, приводящего к неточному или эффективному решению задачи |
| Ошибка анализа | Неполный учет ситуаций, которые могут возникнуть; логические ошибки |
| Семантические ошибки | Непонимание порядка выполнения оператора |
| Синтаксические ошибки | Нарушение правил, определяемых языком программирования |
| Ошибки при выполнении операций | Слишком большое число, деление на ноль, извлечение квадратного корня из отрицательного числа и т. п. |
| Ошибки в данных | Неудачное определение возможного диапазона изменения данных |
| Опечатки | Перепутаны близкие по написанию символы, например, цифра 1 и буквы I, l |
| Ошибки ввода-вывода | Неверное считывание входных данных, неверное задание форматов данных |
8.11. Является ли отсутствие синтаксических ошибок свидетельством правильности программы?
Обычно синтаксические ошибки выявляются на этапе трансляции. Многие же другие ошибки транслятору выявить невозможно, так как транслятору неизвестны замыслы программиста.
Отсутствие сообщений машины о синтаксических ошибках является необходимым,
но не достаточным условием, чтобы считать программу правильной.
8.12. Какие ошибки не обнаруживаются транслятором?
Существует множество ошибок, которые транслятор выявить не в состоянии, если используемые в программе операторы сформированы верно. Приведем примеры таких ошибок.
Все эти ошибки обнаруживаются с помощью тестирования.
8.13. В чем заключается сопровождение программы?
Сопровождение программ это работы, связанные с обслуживанием программ
в процессе их эксплуатации.
Применительно ко многим программам работы по сопровождению поглощают более половины затрат, приходящихся на весь период времени существования программы (начиная от выработки первоначальной концепции и кончая моральным ее устареванием) в стоимостном выражении.
Программа, предназначеная для длительной эксплуатации, должна иметь соответствующую документацию и инструкцию по её использованию.
8.14. Вопросы для самоконтроля
8.1. Какие основные этапы включает в себя решение задач на компьютере?
8.2. Какие этапы компьютерного решения задач осуществляются без участия компьютера?
8.3. Что называют математической моделью объекта или явления?
8.4. Почему невозможно точное исследование поведения объектов или явлений?
8.5. Какие способы моделирования осуществляются с помощью компьютера?
8.6. Из каких последовательных действий состоит процесс разработки программы?
8.7. Доказывает ли получение правдоподобного результата правильность программы?
8.8. Какие ошибки могут остаться невыявленными, если не провести проверку (просмотр, прокрутку) программы?
8.9. Чем тестирование программы отличается от её отладки?
8.10. Каким образом программа-отладчик помогает исследовать поведение программы в процессе её выполнения?
8.11. Как следует планировать процесс отладки программы?
8.12. Можно ли с помощью тестирования доказать правильность программы?
8.13. На какой стадии работы над программой вычисляются эталонные результаты тестов?
8.14. Назовите основные этапы процесса тестирования.
8.15. В чём заключается отличие синта ксических ошибок от семантических?
8.16. О чём свидетельствует отсутствие сообщений машины о синтаксических ошибках?
8.17. Какие разновидности ошибок транслятор не в состоянии обнаружить?
8.18. Для чего программам требуется сопровождение?
8.15. Упражнения
Составьте системы тестов для решения следующих задач:
8.1. Найдите наибольший общий делитель двух заданных целых чисел.
8.2. Найдите наименьшее общее кратное двух заданных целых чисел.
8.3. Определите, является ли заданное число нечетным двузначным числом.
8.4. Заданы площади квадрата и круга. Определите, поместится ли квадрат в круге.
8.5. Решите биквадратное уравнение.
8.6. Найдите среднее арифметическое положительных элементов заданного одномерного массива.
8.7. Элементы заданного одномерного массива разделите на его первый элемент.
8.8. Определите, лежит ли заданная точка на одной из сторон треугольника, заданного координатами своих вершин.
8.9. Определите, имеют ли общие точки две плоские фигуры треугольник с заданными координатами его вершин и круг заданного радиуса c центром в начале координат.
8.10. Задано целое А > 1. Найдите наименьшее целое неотрицательное k, при котором 2 k > А.
8.11. Дана последовательность целых чисел. Определите, со скольких чётных чисел она начинается.
8.12. В заданном двумерном массиве найдите количество строк, не содержащих нули.
8.13. Определите, сколько строк заданного двумерного массива содержат элементы из заданного диапазона.
8.14. Преобразуйте число, заданное в римской системе счисления, в число десятичной системы.
Источник
Обновлено: 24.04.2023
Алгоритм чаще всего представляется в форме блок-схемы ввиду её наглядности и универсальности. Результатом этапа алгоритмизации является блок-схема.
Что является результатом на этапе программирования?
Программирование является четвертым этапом решения задачи с использованием компьютера. На четвертом этапе алгоритм записывается на одном из языков программирования. Результатом этого этапа является программа.
Что является результатом на этапе компьютерного эксперимента?
Что происходит на этапе компьютерного эксперимента? . После тестирования проводится компьютерный эксперимент, в результате которого проверяется работа программы в реальных условиях. Результатом этого этапа является программа, готовая к использованию для решения, поставленной на этапе постановки, задачи.
Что происходит на этапе компьютерного?
Компьютерный эксперимент является последним этапом решения задачи с использованием компьютера. На этапе эксперимента (тестирования, отладки) написанную программу проверяют на работоспособность, исправляют найденные ошибки. . Это и есть отладка. Она продолжается до момента когда программа будет работать правильно.
Что является результатом процесса формализации?
Результатом этапа «формализация» решения задачи на компьютере является математическая модель, которая описывает явление или объект, которые фигурируют в условии. То есть записать при помощи формул соотношения между данными задачи и понять, при помощи каких формул можно найти результирующие данные из исходных.
Какой этап решения задачи на компьютере по вашему мнению является наиболее трудоемким?
8. Какой этап решения задачи на ПК является наиболее трудоемким? . В нем нужно записать известные связи между исходными данными и результатами, тем самым решив задачу с помощью математических соотношений.
Что происходит на этапе программирование?
Что происходит на этапе программирования? . Этап программирования заключается в составлении программы по алгоритму, разработанному на этапе алгоритмизации. Подбирается язык программирования – процедурные или объектно-ориентированный. Для разработки драйверов устройств чаще используется машинный язык (ассемблер).
Сколько этапов насчитывает решение задачи на компьютере?
- Постановка задачи. Включает в себя: .
- Моделирование. .
- Построение алгоритма. .
- Программирование. .
- Отладка и тестирование программы. .
- Анализ результатов.
Что осуществляется на этапе программирования?
На этапе создания происходит разработка интерфейса программы (кнопки, иконки, расположение и т. д.); создаётся программный код — пишется программа, реализующая ранее выбранный алгоритм; осуществляются отладка и тестирование программы.
Что происходит на этапе постановки задачи?
Постановка задачи является первым этапом решения задачи с использованием компьютера. На первом этапе обычно осуществляется постановка задачи, происходит осознание её условия. При этом должно быть чётко определено, что дано (какие исходные данные известны, какие данные допустимы) и что требуется найти в решаемой задаче.
На каком этапе записывается алгоритм на одном из языков программирования?
На четвёртом этапе алгоритм записывается на одном из языков программирования. На пятом этапе осуществляется отладка и тестирование программы. Этап отладки и тестирования также называют компьютерным экспериментом.
На каком этапе записывается алгоритм?
На третьем этапе осуществляется построение алгоритма — чёткой инструкции, задающей необходимую последовательность действий для решения задачи. Алгоритм чаще всего представляется в форме блок-схемы ввиду её наглядности и универсальности.
Какие этапы компьютерного решения задач осуществляется без участия компьютера?
- синтаксическая отладка;
- отладка семантики и логической стpуктуpы;
- тестовые pасчеты и анализ pезультатов тестиpования;
- совершенствование пpогpаммы.
Что происходит на этапе формализации?
На этапе формализации строится математическая модель задачи. Определяется к какому классу относится рассматриваемая задача. Записываются известные связи между исходными данными и результатами с помощью математических соотношений. Выбирается наиболее подходящий способ для решения задачи.
На каком этапе определяются исходные данные?
На первом этапе анализируется условие задачи, определяются исходные данные и результаты, устанавливается зависимость между величинами, рассматриваемыми в задаче. Некоторые задачи имеют множество способов решения, поэтому необходимо выбрать способ решения (сделать постановку задачи, составить модель задачи).
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Какой этап решения задачи на компьютере, по вашему мнению, является наиболее трудоемким?
Ответ
По моему мнению, наиболее трудоемкий этап это формализация, так как если стоит достаточно сложная задача, гораздо труднее найти пути ее решения, чем воплотить их потом в жизнь алгоритмом или программой. Если ты хорошо знаешь язык программирования, то написать программу по готовому алгоритму не составит труда.
Но тем не менее если задача достаточно проста в смысле определения пути решения, но требует обработки большого числа различной информации, то более трудоемким будет этап программирования.
Смотря какая задача.
Речь разумеется идёт об отладке, но это когда что-нибудь программируем, но «решением задачи» может быть и написание в ворде сочинения на тему «Раскольников как типичный представитель российского студенчества».
Тогда самым трудоёмким будет первый этап — научиться выполнять глупые приказы.
это в разделе «алгоритмизация и программирование» тут о программировании,
а что такое отладкка?
заранее большое спасибо)
inga zajonc Искусственный Интеллект (155270) Ай-яй-яй. Отладка — это поиск и исправление ошибок в программе. Отладка строго говоря прекращается, когда перестают выходить «обновления» к допустим виндовс. Потому как эти обновления, а на самом деле заплатки, что-то там «устраняют».
Какой этап решения задачи на компьютере является наиболее трудоемким.

Начальный этап, потом будет легче.

УСТАНОВИТЕ СООТВЕТСТВИЕ МЕЖДУ ЭТАПАМИ РЕШЕНИЯ ЗАДАЧИ НА КОМПЬЮТЕРЕ И ИХ РЕЗУЛЬТАТАМИ : ЭТАПЫ : 1?
УСТАНОВИТЕ СООТВЕТСТВИЕ МЕЖДУ ЭТАПАМИ РЕШЕНИЯ ЗАДАЧИ НА КОМПЬЮТЕРЕ И ИХ РЕЗУЛЬТАТАМИ : ЭТАПЫ : 1.
Постановка задачи 2.
Разработка алгоритма 4.
Отладка, тестирование 6.
Выполнение расчетов РЕЗУЛЬТАТЫ : а) алгоритм б) программа в) словесная информационная модель г) результат расчетов д) математическая модель е) уточненная математическая модель.

Перечислите основны этапы подготовки текстового докуменка на компьютере?
Перечислите основны этапы подготовки текстового докуменка на компьютере?

В состав каких систем входит подсистема «компьютер»?
В состав каких систем входит подсистема «компьютер»?
Для каких систем компьютер является надсистемой?

По силам ли одному специалисту реализация всех этапов решения сложной практической задачи по компьютеру?
По силам ли одному специалисту реализация всех этапов решения сложной практической задачи по компьютеру.

Что является внешней памятью компьютера?
Что является внешней памятью компьютера?

Основные этапы развития компьютеров?
Основные этапы развития компьютеров?

Как правило, сложные практические задачи решаются большими коллективами разработчиков?
Как правило, сложные практические задачи решаются большими коллективами разработчиков.
Отдельные группы в этих коллективах специализируются на выполнении одного или нескольких этапов решения задачи.
Нужно ли в таком случае им иметь представление обо всех этапах решения задачи с использованием компьютера обоснуйте точку зрения.

Этап подготовки документа на компьютере, при котором вы просматриваете его, исправляете обнаруженные ошибки и вносите необходимые изменения?
Этап подготовки документа на компьютере, при котором вы просматриваете его, исправляете обнаруженные ошибки и вносите необходимые изменения.

Что относится ко 2 — му этапу решения задач на ЭВМ?
Что относится ко 2 — му этапу решения задач на ЭВМ.

Этап методологии решения проблемы, где определяются требования для решения, является А) Дизайн Б) Анализ В) Оценка Г) Разработка?
Этап методологии решения проблемы, где определяются требования для решения, является А) Дизайн Б) Анализ В) Оценка Г) Разработка.

1 1920 бит 33. 792 кб 26. 624 мб 196 байт 3. 584 2 700 мб равно 716800 716800 : 256 равно 2800 3 600 * 3 равно 1800 мб 2гб равно 2048 мб (2 * 1024) 1800 меньше 2048 значит не поместится.

Я Думаю, что это буквы русскогоалфавита.

12122 34 : 2 = 17 17 — 3 = 14 14 : 2 = 7 7 — 3 = 4 4 — 3 = 1.

У них много минусов Подумай)).

На основании словесного алгоритма рисуется блок — схема : •Вводим новую переменную х2 = k•Составляем квадратное уравнение с новой переменной аk2 + вk + с = 0•Решаем квадратное уравнение через дискриминант•Решаем квадратное уравнение•Записываем ответ.

Примеры : 1) Вышел на улицу — неполная Вася вышел гулять на площадке перед домом в шесть часов вечера — полная 2) Поставил два за поведение — неполная Дворник ради шутки поставил два за поведение в дневник мальчика — полная.

98 байт без «! » знака, с ним 100 байт считаешь все, буквы, пробелы, знаки и все, готово.

Информатизация – это производное от слова информация. Информатизация – это процесс получения, использования, хранения, передачи информации. На протяжении ХХ века сменялось множество способов обмена информацией. Если в XIX веке носителем информации..


В данном видеоуроке рассматривается решение задачи с помощью компьютера, его этапы, порядок действий на каждом этапе и их особенности.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока «Решение задач на компьютере. Этапы решения задачи на компьютере»
Решение любой задачи с помощью компьютера можно разделить на пять основных этапов:
1. Постановка задачи.
2. Формализация задачи.
3. Создание алгоритма.
5. Тестирование и отладка.
Постановка задачи. На этапе постановки задачи нужно понять условие задачи, выделить исходные и результирующие данные и понять отношения между ними. Проще говоря, нужно ответить на вопросы:
Формализация задачи. Во время этого этапа нужно записать описательную информационную модель, созданную на этапе постановки задачи, каким-либо формальным языком, например математическими формулами, и адаптировать эти формулы для решения данной задачи. То есть нам нужно записать при помощи формул соотношения между данными задачи и понять, при помощи каких формул можно найти результирующие данные из исходных. Иначе говоря, создать математическую модель, описывающую явление или объект, которые фигурируют в условии.
При создании алгоритма должны быть соблюдены два условия:
· Созданный алгоритм должен быть конкретной последовательностью действий, которая приводит к получению результирующих данных из исходных.
· Созданный алгоритм должен быть понятен человеку, который будет писать по нему программу.
Чаще всего алгоритм записывается в форме блок-схемы, потому что данная форма записи достаточно наглядна и универсальна.

Пример блок-схемы
На этапе программирования алгоритм записывается с помощью какого-нибудь языка программирования. То есть результатом работы на данном этапе должна быть программа. Мы будем писать программы на языке Pascal.

Пример программы на языке Pascal
На этапе тестирования и отладки проверяется, работает ли программа, если работает, то правильно ли. Проверяется отсутствие ошибок в программе. Ошибки делятся на синтаксические, которые связаны с нарушением правил записи программы на конкретном языке программирования, и логические, которые могут быть связаны с недостаточно точной математической моделью, недостаточно точным алгоритмом или же неточной записью алгоритма на языке программирования. Синтаксические ошибки находятся при помощи программных средств, а логические ошибки находятся с помощью тестов.
Тест – это набор конкретных значений исходных данных, при которых известен ожидаемый результат работы программы.
Обратим внимание на то, что этапы постановки и формализации задачи могут требовать наличия некоторых знаний из предметной области задачи. Например, если наша задача из области авиастроения – то без знаний из этой области мы не сможем узнать отношений между исходными и результирующими данными, а тем более записать их в виде формул.
Этапы создания алгоритма и программирования требуют наличия знаний по программированию. Так как на третьем этапе определяется каким образом будет решаться та или иная подзадача. А от этого зависит скорость работы программы, и количество потребляемых ею ресурсов системы, например оперативной памяти. На четвёртом этапе записать алгоритм тоже можно различными способами.
На этапе тестирования и отладки требуются как знания по предметной области, так и некоторое знание основ программирования. Так как без знаний в предметной области мы не можем знать результирующих данных в тестах, а без знаний в программировании мы не сможем отыскать ошибки и составить наиболее полный набор тестов, учитывающий все частные случаи и исключения.
Читайте также:
- Порядок организации и осуществления образовательной деятельности в доу 2021
- Какие вы знаете народные приметы приближения разрушительных природных явлений обж кратко
- Почему в каспийском море вода соленая кратко
- Многообразие внешних устройств подключаемых к компьютеру план урока
- Каким образом данные эмбриологии могут служить доказательствами эволюции кратко
Алгоритмизация и
программирование
Введение
Каждый из нас постоянно
решает множество задач: как быстрее собраться на работу, как лучше спланировать
дела текущего дня и многие другие. Некоторые задачи мы решаем автоматически,
так как на протяжении многих лет привыкли к их выполнению, другие требуют
длительного размышления над решением, но в любом случае, решение каждой задачи
всегда делится на простые действия.
Алгоритмизация– это техника
разработки алгоритма для решения задач на компьютере. Изобразительные средства
для представления или описания алгоритма.
Понятие алгоритма,
являющееся фундаментальным в математике и информатике, возникло задолго до
появления средств вычислительной техники. Слово «алгоритм» появилось в средние
века, когда европейцы познакомились со способами выполнения арифметических
действий в десятичной системе счисления, описанными узбекским математиком
Муххамедом бен Аль-Хорезми («аль-Хорезми» — человек из города Хорезми); в
настоящее время город Хива в Хорезмской области Узбекистана). Слово алгоритм –
есть результат европейского произношения слов аль-Хорезми.
Первоначально под
алгоритмом понимали способ выполнения арифметических действий над десятичными
числами. В дальнейшем это понятие стали использовать для обозначения любой
последовательности действий, приводящей к решению поставленной задачи.
Чтобы решать задачи на
компьютере, необходимо владеть языком программирования, обладать знаниями в
области информационного моделирования и алгоритмизации.
Этапы
решения задачи на компьютере
На первом этапе обычно осуществляется
постановка задачи, происходит осознание её условия. При этом должно быть чётко
определено, что дано, какие исходные данные известны, какие являются
параметрами к условию задачи, и что требуется найти в решаемой задаче. Также
должны быть чётко выделены существенные свойства рассматриваемого объекта, указаны
связи между исходными данными и результатами.
На втором этапе описательная информационная модель
формализуется, т.е записывается с помощью некоторого формального языка.
В свою очередь этапы чётко зависят от полученного результата:
Этап = Результат
Поставка задачи Словесная
информационная модель
Формализация Математическая
модель
Алгоритмизация Алгоритм
Программирование Программа
Отладка, тестирование Уточнённая
модель
Выполнение расчётов Ответы на поставленные в задаче
вопросы
Для правильной установки этапов, требуется:
·
понять, к какому классу
принадлежит рассматриваемая задача;
·
записать известные связи
между исходными данными и результатами с помощью математических соотношений;
·
выбрать наиболее
подходящий способ для решения задачи.
На третьем этапе
осуществляется построение алгоритма – чёткой инструкции, задающей необходимую
последовательность действий для решения задачи. Алгоритм чаще всего
представляется в форме блок-схемы ввиду её наглядности и универсальности.
На четвёртом этапе алгоритм записывается
на одном из языков программирования. Важно отметить, что основной ошибкой
многих пользователей компьютером, является мнение о том, что HTML – это язык программирования. На самом деле HTML – это
язык разметки.
На пятом этапе осуществляется отладка и
тестирование программы.
Отладка программы – это процесс проверки
работоспособности программы и исправления обнаруженных при этом ошибок.
Ошибки могут быть связаны с нарушением правил
записи программы на конкретном языке программирования, таким образом, на Pascal’e используется
в качестве ввода информации на экран команда “write/writeln”,
когда в это же время, на C эта же команда обозначается с помощью “printf”.
На шестом этапе по уточнённой программе
проводятся необходимые вычисления, результаты которых позволяют ответить на
поставленные в задаче вопросы.
Рассмотренные этапы являются основой разработки, и
написания программного обеспечения, но при этом называются они несколько иначе.

![]()
![]()

![]()
![]()
![]()

![]()
![]() Этапы разработки программного обеспечения:
Этапы разработки программного обеспечения:
На этапе подготовки разработчик уточняет у
заказчика требования к программному продукту, осуществляет предварительное
планирование этапов работ, сроков, ресурсов и стоимости разработки.
На этапе проектирования составляется требования к
программе, определяются её технические характеристики, выбираются алгоритмы
реализации программы.
На этапе создания происходит разработка
интерфейса программы (кнопки, иконки, расположение и т.д); создается
программный код – пишется программа, реализующая ранее выбранный алгоритм; осуществляются
отладка и тестирование программы. На этом же этапе создается пакет документации,
включающий различные описания, инструкции и руководства. Наличие подробной
документации обеспечивает в том числе возможность передачи накопленных знаний
другим разработчикам.
На этапе поддержки происходит установка
разработанного программного обеспечения (внедрение), исправление выявленных
ошибок и поддержка пользователей (сопровождение).
Задачи
Разберем
последовательность этапов решения задач на компьютере, на таких языках
программирования как Pascal и C.
Начнем пожалуй,
с C:
Напишите
программу, которая высчитывает плату за пользование кредитом после того как
введены сумма кредита, процентная годовая ставка и срок кредита в днях = сумма
* процентная ставка * (срок кредита в днях / 365)
Первый этап.
Дано:
Параметры – сумма кредита; процентная
годовая ставка; срок кредита в днях;
Срок кредита в днях – Сумма кредита * Процентная
годовая ставка * (Срок кредита в днях / 365).
Где * — умножение, а / — деление.
Требуется найти: Плату за пользование кредитом.
Второй этап.
В данной ситуации мы имеет дело с формулой, по которой мы должны
рассчитать поставленное нам условие в задаче, а именно:
Срок кредита в днях – Сумма кредита *
Процентная годовая ставка * (Срок кредита в днях / 365).
Третий этап.
В данном этапе представим алгоритм решения
задачи в виде блок-схемы:
 |
|||||||||||
 |
|||||||||||
 |
|||||||||||
 |
Четвёртый этап.
Запишем данный алгоритм на языке программирования C в программе
“Microsoft Visual Studio”.
#include <stdio.h>
int main() {
float Sum, PY, DateOfCredit;
printf(«Enter the amount of you credit =
n»);
// введите сумму кредита
scanf_s(«%f», &Sum);
printf(«Enter the annual interest rate =
n»);
// введите процентную годовую ставку
scanf_s(«%f», &PY);
printf(«Enter the date of you credit =
n»);
// введите срок кредита
scanf_s(«%f», &DateOfCredit);
printf(«Your charge is = %1f», Sum * PY *
(DateOfCredit / 365));
return 0;
}
Пятый этап.
Протестировать составленную программу можно, используя информацию, которую
вводит пользователь в поле для ввода данных.
Шестой этап
Выполнив программу несколько раз при различных исходных данных, можно
сделать вывод: чем больше числа, которые вводит пользователь, тем больше плата
за использование кредита.
Следующая программа будет написана на Pascal:
Водитель
автомобиля, движущегося с некоторой постоянной скоростью, увидев красный свет
светофора, нажал на тормоз. После этого скорость автомобиля стала уменьшаться
каждую секунду на 5 метров. Требуется найти расстояние, которое автомобиль
пройдет до полной остановки.
Первый этап.
Дано:
![]() –
–
начальная скорость;
![]() –
–
конечная скорость (равно нулю, так как автомобиль остановился);
![]() –
–
ускорение (равно -5м/c²).
Требуется найти: ![]() – расстояние, которое автомобиль пройдёт до
– расстояние, которое автомобиль пройдёт до
полной остановки.
Второй этап.
В данной ситуации мы имеем дело с прямолинейным равноускоренным движением
тела. Формула для перемещения при этом имеет вид:
![]()
Упрости эту формулу с учётом того, что конечная
скорость равна нулю: ![]() . При
. При
![]() =
=
5м/c² получим: ![]() (при
(при
условии задания скорости в метрах в секунду и вычислении пути в метрах).
Третий этап.
![]()
![]()
![]()
![]()




 Представим алгоритм решения задачи в виде блок-схемы:
Представим алгоритм решения задачи в виде блок-схемы:
Четвертый этап.
Запишем данный алгоритм на языке программирования Паскаль:
program
n_1;
var
v0, s: real;
begin
writeln(‘Вычисление длины пути торможения автомобиля’);
write(‘Введите начальную скорость (м/c)>>’);
readln (v0);
s:=v0*v0/10;
writeln(‘До полной остановки автомобиль пройдет — ‘, s:8:4, ‘
м. ’)
end.
Пятый этап.
Протестировать составленную программу можно, используя информацию, что
при скорости 72км/ч с начала торможения до полной остановки автомобиль проходит
40 метров.
Шестой этап.
Выполнив программу несколько раз при различных исходных данных, можно
сделать вывод: чем больше начальная скорость автомобиля, тем большее расстояние
он пройдет с начала торможения до полной остановки.
Применяя компьютер для решения задач, всегда следует
помнить, что наряду с огромным быстродействием и абсолютной исполнительностью у
компьютера отсутствуют интуиция и чувство здравого смысла и он способен решать
только ту задачу, программу решения которой ему подготовил человек.
Источники
Учебник Л.Л.Босова
и А.Ю.Босова — Информатика 9 класс (дата обращения: 19.10.2020)
Россия // Учебник Л.Л.Босова и А.Ю.Босова [2020]. Дата обновления: 15.10.2020.
URL: https://moodle.kstu.ru/mod/page/view.php?id=47344 (дата
обращения: 19.10.2020).
Россия // Deitel C —
Задачи — Глава 3 [2020]. Дата обновления: 18.10.2020.
URL: http://isec.nayanovaacademy.ru/wiki/Deitel_C_-_Задачи_-_Глава_3#03.19 (дата
обращения: 19.10.2020).
Автор вопроса: Марсель Василюк
Опубликовано: 02/04/2023
На каком этапе разработки программы составляется алгоритм решения задачи?
У нас есть 22 ответов на вопрос На каком этапе разработки программы составляется алгоритм решения задачи? Скорее всего, этого будет достаточно, чтобы вы получили ответ на ваш вопрос.
- На каком этапе записывается алгоритм?
- В каком порядке должны выполняться следующие шаги решения расчетной задачи?
- Сколько этапов решения задачи на компьютере?
- На каком этапе решения задачи на компьютере осуществляется запись алгоритма на одном из языков программирования?
- На каком этапе определяются исходные данные?
- На каком этапе формулируется цель решения задачи и подробно описывается ее содержание?
- Какие этапы решения задачи осуществляются без компьютера?
- На каком этапе разработки программы составляется алгоритм решения задачи? Ответы пользователей
- На каком этапе разработки программы составляется алгоритм решения задачи? Видео-ответы
Отвечает Евгений Бочаров
5. Построение алгоритма — на данном этапе составляется алгоритм решения задачи, в соответствии с выбранным методом решения.
На каком этапе записывается алгоритм?
На третьем этапе осуществляется построение алгоритма — чёткой инструкции, задающей необходимую последовательность действий для решения задачи. Алгоритм чаще всего представляется в форме блок-схемы ввиду её наглядности и универсальности.
В каком порядке должны выполняться следующие шаги решения расчетной задачи?
Этапы решения задач на компьютереПостановка задачи.Формализация задачи.Построение алгоритма.Составление программы на языке программирования.Отладка и тестирование программы.Проведение расчётов и анализ полученных результатов.
Сколько этапов решения задачи на компьютере?
Решение задач с помощью компьютера включает в себя следующие этапы:Постановка задачи. Включает в себя: … Моделирование. … Построение алгоритма. … Программирование. … Отладка и тестирование программы. … Анализ результатов.
На каком этапе решения задачи на компьютере осуществляется запись алгоритма на одном из языков программирования?
На третьем этапе осуществляется построение алгоритма — чёткой инструкции, задающей необходимую последовательность действий для решения задачи. Алгоритм чаще всего представляется в форме блок-схемы ввиду её наглядности и универсальности. На четвёртом этапе алгоритм записывается на одном из языков программирования.
На каком этапе определяются исходные данные?
2.1. На первом этапе обычно осуществляется постановка задачи, происходит осознание её условия. При этом должно быть чётко определено, что дано (какие исходные данные известны, какие данные допустимы) и что требуется найти в решаемой задаче.
На каком этапе формулируется цель решения задачи и подробно описывается ее содержание?
Постановка задачи — формулируется цель решения задачи, подробно описывается ее содержание; проводится анализ условий, при которых решается поставленная задача, выявляется область определения входных параметров задачи.
Какие этапы решения задачи осуществляются без компьютера?
Решение задач с помощью компьютера включает в себя следующие основные этапы, часть из которых осуществляется без участия компьютера….Пpогpаммиpование:выбор языка программирования;уточнение способов организации данных;запись алгоpитма на выбpанном языке пpогpаммиpования.
Отвечает Вячеслав Эгромжан
На этом уроке мы обсудим основные этапы решения задач с помощью компьютера, … математической модели (с последующей корректировкой алгоритма и программы).
Отвечает Нонна Григорьева
Если возникает ситуация, когда поставленную задачу можно решить несколькими способами, то само собой, возможны множество разных вариантов алгоритма решения.
Отвечает Алина Савко
Возможно, что задача решается точно (аналитически), и без компьютера можно обойтись. Уже на этапе постановки надо учитывать эффективность алгоритма решения …
Отвечает Мансор Смирнов
разработка структур данных. … доработка программы для решения конкретных задач; … Массовость. Алгоритм решения задачи разрабатывается в общем виде, …
Отвечает Алексей Силла
При составлении программы алгоритм решения задачи переводится на конкретный язык программирования, для которого обычно используются языки высокого уровня, …
Отвечает Вячеслав Бурзаковский
4. Разработка алгоритма. Процесс обработки данных разбивается на отдельные самостоятельные блоки и определяется последовательность выполнения этих блоков. Для …
Отвечает Алексей Алимов
На этапе проектирования составляются требования к программе, определяются её технические характеристики, выбираются алгоритмы реализации программы. На этапе …
Отвечает Павел Иванов
2) математическая постановка задачи (формализация задачи);. 3) разработка алгоритма (алгоритмизация);. 4) кодирование;. 5) реализация программы на …
Отвечает Кристина Сухорукова
2.Разработка или выбор алгоритма решения поставленной задачи. 3.Написание программы. 4.Отладка. 5.Тестирование. 6.Оформление документации на программу. 1).
Как БЫСТРО изучить АЛГОРИТМЫ и научиться решать задачи? Книги, сайты, инструменты
Алгоритмы и структуры данных. Быстрый путь. Книги, сайты и инструменты, которые позволят быстро прокачать …

Решение задачи на компьютере. Последовательное конструирование алгоритма
Ученики уже начали изучение программирования и успели решить несколько задач с использованием компьютера, но пора …

Алгоритмы: от последовательности действий до решения сложной задачи [GeekBrains]
Алгоритмы: от последовательности действий до решения сложной задачи. На вебинаре мы рассмотрим: — Понятие …
![Алгоритмы: от последовательности действий до решения сложной задачи [GeekBrains]](https://i.ytimg.com/vi/cdA-rsb1vkk/hq720.jpg?sqp=-oaymwEcCOgCEMoBSFXyq4qpAw4IARUAAIhCGAFwAcABBg==&rs=AOn4CLB66OhFM-8NCXt7Akr3Bj4J7dL-8A)
видеоурок 8 класс тестирование программы
Цели обучения: 8.3.1.1- создавать модели задач в интегрированной среде разработки программ (C/C++, Python, Delphi, …

Как научиться строить алгоритмы решения задач по 1С
ЧАСТЬ 2, ПРОДОЛЖЕНИЕ: https://youtu.be/BfKX8E2pKgk.

Алгори́тм (лат. algorithmi — от имени среднеазиатского математика Аль-Хорезми[1]) — совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения определённой задачи. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Независимые инструкции могут выполняться в произвольном порядке, параллельно, если это позволяют используемые исполнители.
Ранее в русском языке писали «алгорифм», сейчас такое написание используется редко, но тем не менее имеет место исключение (нормальный алгорифм Маркова).
Часто в качестве исполнителя выступает компьютер, но понятие алгоритма необязательно относится к компьютерным программам — так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек (а может быть и некоторый механизм, например, ткацкий или токарный станок с числовым управлением).
Можно выделить алгоритмы вычислительные (далее речь в основном идёт о них) и управляющие. Вычислительные алгоритмы, по сути, преобразуют некоторые начальные данные в выходные, реализуя вычисление некоторой функции. Семантика управляющих алгоритмов существенным образом может отличаться и сводиться к выдаче необходимых управляющих воздействий либо в заданные моменты времени, либо в качестве реакции на внешние события (в этом случае, в отличие от вычислительного алгоритма, управляющий может оставаться корректным при бесконечном выполнении).
Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако в явном виде понятие алгоритма сформировалось лишь в начале XX века.
Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений[2] или «эффективного метода»[3]; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Чёрча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга.
История термина[править | править код]


Современное формальное определение вычислительного алгоритма было дано в 30—50-е годы XX века в работах Тьюринга, Поста, Чёрча (тезис Чёрча — Тьюринга), Н. Винера, А. А. Маркова.
Само слово «алгоритм» происходит от имени персидского (хорезмского и мавераннахрского) учёного аль-Хорезми. Около 825 года он написал сочинение Китаб аль-джебр валь-мукабала («Книга о сложении и вычитании»), из оригинального названия которого происходит слово «алгебра» (аль-джебр — восполнение). В этой книге впервые дал описание придуманной в Индии позиционной десятичной системы счисления. Персидский оригинал книги не сохранился. Аль-Хорезми сформулировал правила вычислений в новой системе и, вероятно, впервые использовал цифру 0 для обозначения пропущенной позиции в записи числа (её индийское название арабы перевели как as-sifr или просто sifr, отсюда такие слова, как «цифра» и «шифр»). Приблизительно в это же время индийские цифры начали применять и другие арабские учёные.
В первой половине XII века книга аль-Хорезми в латинском переводе проникла в Европу. Переводчик, имя которого до нас не дошло, дал ей название Algoritmi de numero Indorum («Алгоритми о счёте индийском») — таким образом, латинизированное имя среднеазиатского учёного было вынесено в заглавие книги. Сегодня считается, что слово «алгоритм» попало в европейские языки именно благодаря этому переводу. В течение нескольких следующих столетий появилось множество других трудов, посвящённых всё тому же вопросу — обучению искусству счёта с помощью цифр, и все они имели в названии слово algoritmi или algorismi.
Про аль-Хорезми позднейшие авторы ничего не знали, но поскольку первый перевод книги начинается словами: «Dixit algorizmi: …» («Аль-Хорезми говорил: …»), всё ещё связывали это слово с именем конкретного человека. Очень распространённой была версия о греческом происхождении книги. В англо-норманнской рукописи XIII века, написанной в стихах, читаем:
Алгоризм был придуман в Греции.
Это часть арифметики.
Придуман он был мастером по имени Алгоризм,
который дал ему своё имя.
И поскольку его звали Алгоризм,Он назвал свою книгу «Алгоризм».
Около 1250 года английский астроном и математик Иоанн Сакробоско написал труд по арифметике Algorismus vulgaris, на столетия ставший основным учебником по вычислениям в десятичной позиционной системе счисления во многих европейских университетах. Во введении Сакробоско назвал автором науки о счёте мудреца по имени Алгус (Algus). А в популярной средневековой поэме «Роман о Розе» (1275—1280) Жана де Мена «греческий философ Алгус» ставится в один ряд с Платоном, Аристотелем, Евклидом и Птолемеем! Встречался также вариант написания имени Аргус (Argus). И хотя, согласно древнегреческой мифологии, корабль «Арго» был построен Ясоном, именно этому Арго приписывалось строительство корабля.
«Мастер Алгус» (или Аргус) стал в средневековой литературе олицетворением счётного искусства. И в уже упоминавшейся «Романе о розе», и в известной итальянской поэме «Цветок», написанной Дуранте, имеются фрагменты, в которых говорится, что даже «mestre Argus» не сумеет подсчитать, сколько раз ссорятся и мирятся влюблённые. Английский поэт Джефри Чосер в поэме «Книга герцогини» (1369 г.) пишет, что даже «славный счётчик Аргус» (noble countour Argu) не сможет счесть чудовищ, явившихся в кошмарных видениях герою.
Однако со временем такие объяснения всё менее занимали математиков, и слово algorism (или algorismus), неизменно присутствовавшее в названиях математических сочинений, обрело значение способа выполнения арифметических действий посредством арабских цифр, то есть на бумаге, без использования абака. Именно в таком значении оно вошло во многие европейские языки. Например, с пометкой «устар.» оно присутствует в представительном словаре английского языка Webster’s New World Dictionary, изданном в 1957 г. Энциклопедический словарь Брокгауза и Ефрона предлагает такую трактовку: алгорифм (кстати, до революции использовалось написание алгориѳм, через фиту) производится «от арабского слова Аль-Горетм, то есть корень».
Алгоритм — это искусство счёта с помощью цифр, но поначалу слово «цифра» относилось только к нулю. Знаменитый французский трувер Готье де Куанси (Gautier de Coincy, 1177—1236) в одном из стихотворений использовал слова algorismus-cipher (которые означали цифру 0) как метафору для характеристики абсолютно никчёмного человека. Очевидно, понимание такого образа требовало соответствующей подготовки слушателей, а это означает, что новая система счисления уже была им достаточно хорошо известна.
Многие века абак был фактически единственным средством для практичных вычислений, им пользовались и купцы, и менялы, и учёные. Достоинства вычислений на счётной доске разъяснял в своих сочинениях такой выдающийся мыслитель, как Герберт Аврилакский (938—1003), ставший в 999 г. папой римским под именем Сильвестра II. Новое с огромным трудом пробивало себе дорогу, и в историю математики вошло упорное противостояние лагерей алгорисмиков и абацистов (иногда называемых гербекистами), которые пропагандировали использование для вычислений абака вместо арабских цифр. Интересно, что известный французский математик Николя Шюке (Nicolas Chuquet, 1445—1488) в реестр налогоплательщиков города Лиона был вписан как алгорисмик (algoriste). Но прошло не одно столетие, прежде чем новый способ счёта окончательно утвердился, столько времени потребовалось, чтобы выработать общепризнанные обозначения, усовершенствовать и приспособить к записи на бумаге методы вычислений. В Западной Европе учителей арифметики вплоть до XVII века продолжали называть «магистрами абака», как, например, математика Никколо Тарталью (1500—1557).
Итак, сочинения по искусству счёта назывались Алгоритмами. Из многих сотен можно выделить и такие необычные, как написанный в стихах трактат Carmen de Algorismo (латинское carmen и означает стихи) Александра де Вилла Деи (Alexander de Villa Dei, ум. 1240) или учебник венского астронома и математика Георга Пурбаха (Georg Peurbach, 1423—1461) Opus algorismi jocundissimi («Веселейшее сочинение по алгоритму»).
Постепенно значение слова расширялось. Учёные начинали применять его не только к сугубо вычислительным, но и к другим математическим процедурам. Например, около 1360 г. французский философ Николай Орем (Nicolaus Oresme, 1323/25-1382) написал математический трактат Algorismus proportionum («Вычисление пропорций»), в котором впервые использовал степени с дробными показателями и фактически вплотную подошёл к идее логарифмов. Когда же на смену абаку пришёл так называемый счёт на линиях, многочисленные руководства по нему стали называть Algorithmus linealis, то есть правила счёта на линиях.
Можно обратить внимание на то, что первоначальная форма algorismi спустя какое-то время потеряла последнюю букву, и слово приобрело более удобное для европейского произношения вид algorism. Позднее и оно, в свою очередь, подверглось искажению, скорее всего, связанному со словом arithmetic.
В 1684 году Готфрид Лейбниц в сочинении Nova Methodvs pro maximis et minimis, itemque tangentibus… впервые использовал слово «алгоритм» (Algorithmo) в ещё более широком смысле: как систематический способ решения проблем дифференциального исчисления.
В XVIII веке в одном из германских математических словарей, Vollstandiges mathematisches Lexicon (изданном в Лейпциге в 1747 г.), термин algorithmus всё ещё объясняется как понятие о четырёх арифметических операциях. Но такое значение не было единственным, ведь терминология математической науки в те времена ещё только формировалась. В частности, выражение algorithmus infinitesimalis применялось к способам выполнения действий с бесконечно малыми величинами. Пользовался словом алгоритм и Леонард Эйлер, одна из работ которого так и называется — «Использование нового алгоритма для решения проблемы Пелля» (De usu novi algorithmi in problemate Pelliano solvendo). Мы видим, что понимание Эйлером алгоритма как синонима способа решения задачи уже очень близко к современному.
Однако потребовалось ещё почти два столетия, чтобы все старинные значения слова вышли из употребления. Этот процесс можно проследить на примере проникновения слова «алгоритм» в русский язык.
Историки датируют 1691 годом один из списков древнерусского учебника арифметики, известного как «Счётная мудрость». Это сочинение известно во многих вариантах (самые ранние из них почти на сто лет старше) и восходит к ещё более древним рукописям XVI в. По ним можно проследить, как знание арабских цифр и правил действий с ними постепенно распространялось на Руси. Полное название этого учебника — «Сия книга, глаголемая по-еллински и по-гречески арифметика, а по-немецки алгоризма, а по-русски цифирная счётная мудрость».
Таким образом, слово «алгоритм» понималось первыми русскими математиками так же, как и в Западной Европе. Однако его не было ни в знаменитом словаре В. И. Даля, ни спустя сто лет в «Толковом словаре русского языка» под редакцией Д. Н. Ушакова (1935 г.). Зато слово «алгорифм» можно найти и в популярном дореволюционном Энциклопедическом словаре братьев Гранат, и в первом издании Большой советской энциклопедии (БСЭ), изданном в 1926 г. И там, и там оно трактуется одинаково: как правило, по которому выполняется то или иное из четырёх арифметических действий в десятичной системе счисления. Однако к началу XX в. для математиков слово «алгоритм» уже означало любой арифметический или алгебраический процесс, выполняемый по строго определённым правилам, и это объяснение также даётся в следующих изданиях БСЭ.

Алгоритмы становились предметом всё более пристального внимания учёных, и постепенно это понятие заняло одно из центральных мест в современной математике. Что же касается людей, от математики далёких, то к началу сороковых годов это слово они могли услышать разве что во время учёбы в школе, в сочетании «алгоритм Евклида». Несмотря на это, алгоритм всё ещё воспринимался как термин сугубо специальный, что подтверждается отсутствием соответствующих статей в менее объёмных изданиях. В частности, его нет даже в десятитомной Малой советской энциклопедии (1957 г.), не говоря уже об однотомных энциклопедических словарях. Но зато спустя десять лет, в третьем издании Большой советской энциклопедии (1969 г.) алгоритм уже характеризуется как одна из основных категорий математики, «не обладающих формальным определением в терминах более простых понятий, и абстрагируемых непосредственно из опыта». Как мы видим, отличие даже от трактовки первым изданием БСЭ разительное! За сорок лет алгоритм превратился в одно из ключевых понятий математики, и признанием этого стало включение слова уже не в энциклопедии, а в словари. Например, оно присутствует в академическом «Словаре русского языка» (1981 г.) именно как термин из области математики.
Одновременно с развитием понятия алгоритма постепенно происходила и его экспансия из чистой математики в другие сферы. И начало ей положило появление компьютеров, благодаря которому слово «алгоритм» вошло в 1985 г. во все школьные учебники информатики и обрело новую жизнь. Вообще можно сказать, что его сегодняшняя известность напрямую связана со степенью распространения компьютеров.
Например, в третьем томе «Детской энциклопедии» (1959 г.) о вычислительных машинах говорится немало, но они ещё не стали чем-то привычным и воспринимаются скорее как некий атрибут светлого, но достаточно далёкого будущего. Соответственно и алгоритмы ни разу не упоминаются на её страницах. Но уже в начале 70-х гг. прошлого столетия, когда компьютеры перестали быть экзотической диковинкой, слово «алгоритм» стремительно входит в обиход. Это чутко фиксируют энциклопедические издания. В «Энциклопедии кибернетики» (1974 г.) в статье «Алгоритм» он уже связывается с реализацией на вычислительных машинах, а в «Советской военной энциклопедии» (1976 г.) даже появляется отдельная статья «Алгоритм решения задачи на ЭВМ».
За последние полтора-два десятилетия компьютер стал неотъемлемым атрибутом нашей жизни, компьютерная лексика становится всё более привычной. Слово «алгоритм» в наши дни известно, вероятно, каждому. Оно уверенно шагнуло даже в разговорную речь, и сегодня мы нередко встречаем в газетах и слышим в выступлениях политиков выражения вроде «алгоритм поведения», «алгоритм успеха» или даже «алгоритм предательства». Академик Н. Н. Моисеев назвал свою книгу «Алгоритмы развития», а известный врач Н. М. Амосов — «Алгоритм здоровья» и «Алгоритмы разума». А это означает, что слово живёт, обогащаясь всё новыми значениями и смысловыми оттенками.
Определения алгоритма[править | править код]
Свойства алгоритмов[править | править код]
Различные определения алгоритма в явной или неявной форме содержат следующий ряд общих требований:
- Дискретность — алгоритм должен представлять процесс решения задачи как упорядоченное выполнение некоторых простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, то есть преобразование исходных данных в результат осуществляется во времени дискретно.
- Детерминированность (определённость). В каждый момент времени следующий шаг работы однозначно определяется состоянием системы. Таким образом, алгоритм выдаёт один и тот же результат (ответ) для одних и тех же исходных данных. В современной трактовке у разных реализаций одного и того же алгоритма должен быть изоморфный граф. С другой стороны, существуют вероятностные алгоритмы, в которых следующий шаг работы зависит от текущего состояния системы и генерируемого случайного числа. Однако при включении метода генерации случайных чисел в список «исходных данных» вероятностный алгоритм становится подвидом обычного.
- Понятность — алгоритм должен включать только те команды, которые доступны исполнителю и входят в его систему команд.
- Завершаемость (конечность) — в более узком понимании алгоритма как математической функции, при правильно заданных начальных данных алгоритм должен завершать работу и выдавать результат за определённое число шагов. Дональд Кнут процедуру, которая удовлетворяет всем свойствам алгоритма, кроме, возможно, конечности, называет методом вычисления (англ. computational method)[4]. Однако довольно часто определение алгоритма не включает завершаемость за конечное время[5]. В этом случае алгоритм (метод вычисления) определяет частичную функцию[en]. Для вероятностных алгоритмов завершаемость как правило означает, что алгоритм выдаёт результат с вероятностью 1 для любых правильно заданных начальных данных (то есть может в некоторых случаях не завершиться, но вероятность этого должна быть равна 0).
- Массовость (универсальность). Алгоритм должен быть применим к разным наборам начальных данных.
- Результативность — завершение алгоритма определёнными результатами.
Формальное определение[править | править код]
Разнообразные теоретические проблемы математики и ускорение развития физики и техники поставили на повестку дня точное определение понятия алгоритма.
Первые попытки уточнения понятия алгоритма и его исследования осуществляли в первой половине XX века Алан Тьюринг, Эмиль Пост, Жак Эрбран, Курт Гедель, А. А. Марков, Алонзо Чёрч. Было разработано несколько определений понятия алгоритма, но впоследствии было выяснено, что все они определяют одно и то же понятие (см. Тезис Чёрча — Тьюринга)[6]
Российский математик, основоположник структурной лингвистики в Советском Союзе В. А. Успенский считал, что понятие алгоритма впервые появилось у Эмиля Бореля в 1912 году, в статье об определённом интеграле. Там он написал о «вычислениях, которые можно реально осуществить», подчеркивая при этом: «Я намеренно оставляю в стороне большую или меньшую практическую деятельность; суть здесь та, что каждая из этих операций осуществима в конечное время при помощи достоверного и недвусмысленного метода»[7].
Машина Тьюринга[править | править код]
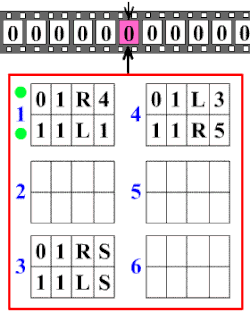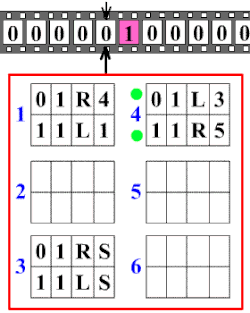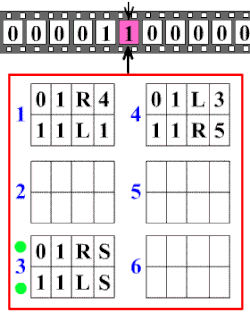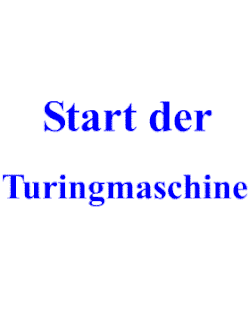
Основная идея, лежащая в основе машины Тьюринга, очень проста. Машина Тьюринга — это абстрактная машина (автомат), работающая с лентой отдельных ячеек, в которых записаны символы. Машина также имеет головку для записи и чтения символов из ячеек, которая может двигаться вдоль ленты. На каждом шаге машина считывает символ из ячейки, на которую указывает головка, и, на основе считанного символа и внутреннего состояния, делает следующий шаг. При этом машина может изменить своё состояние, записать другой символ в ячейку или передвинуть головку на одну ячейку вправо или влево.[8]
На основе исследования этих машин был выдвинут тезис Тьюринга (основная гипотеза алгоритмов):
Некоторый алгоритм для нахождения значений функции, заданной в некотором алфавите, существует тогда и только тогда, когда функция исчисляется по Тьюрингу, то есть когда её можно вычислить на машине Тьюринга.
Этот тезис является аксиомой, постулатом, и не может быть доказан математическими методами, поскольку алгоритм не является точным математическим понятием.
Рекурсивные функции[править | править код]
С каждым алгоритмом можно сопоставить функцию, которую он вычисляет. Однако возникает вопрос, можно ли произвольной функции сопоставить машину Тьюринга, а если нет, то для каких функций существует алгоритм? Исследования этих вопросов привели к созданию в 1930-х годах теории рекурсивных функций[9].
Класс вычислимых функций был записан в образ, напоминающий построение некоторой аксиоматической теории на базе системы аксиом. Сначала были выбраны простейшие функции, вычисление которых очевидно. Затем были сформулированы правила (операторы) построения новых функций на основе уже существующих. Необходимый класс функций состоит из всех функций, которые можно получить из простейших применением операторов.
Подобно тезису Тьюринга в теории вычислимых функций была выдвинута гипотеза, которая называется тезис Чёрча:
Числовая функция тогда и только тогда алгоритмически исчисляется, когда она частично рекурсивна.
Доказательство того, что класс вычислимых функций совпадает с исчисляемыми по Тьюрингу, происходит в два шага: сначала доказывают вычисление простейших функций на машине Тьюринга, а затем — вычисление функций, полученных в результате применения операторов.
Таким образом, неформально алгоритм можно определить как четкую систему инструкций, определяющих дискретный детерминированный процесс, который ведёт от начальных данных (на входе) к искомому результату (на выходе), если он существует, за конечное число шагов; если искомого результата не существует, алгоритм или никогда не завершает работу, либо заходит в тупик.
Нормальный алгоритм (алгорифм) Маркова[править | править код]
Нормальный алгоритм (алгорифм в авторском написании) Маркова — это система последовательных применений подстановок, которые реализуют определённые процедуры получения новых слов из базовых, построенных из символов некоторого алфавита. Как и машина Тьюринга, нормальные алгоритмы не выполняют самих вычислений: они лишь выполняют преобразование слов путём замены букв по заданным правилам[10].
Нормально вычислимой называют функцию, которую можно реализовать нормальным алгоритмом. То есть алгоритмом, который каждое слово из множества допустимых данных функции превращает в её начальные значения[11]..
Создатель теории нормальных алгоритмов А. А. Марков выдвинул гипотезу, которая получила название принцип нормализации Маркова:
Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует некоторый алгоритм, когда функция нормально исчисляемая.
Подобно тезисам Тьюринга и Черча, принцип нормализации Маркова не может быть доказан математическими средствами.
Стохастические алгоритмы[править | править код]
Однако приведённое выше формальное определение алгоритма в некоторых случаях может быть слишком строгим. Иногда возникает потребность в использовании случайных величин[12]. Алгоритм, работа которого определяется не только исходными данными, но и значениями, полученными из генератора случайных чисел, называют стохастическим (или рандомизированным, от англ. randomized algorithm)[13]. Стохастические алгоритмы часто бывают эффективнее детерминированных, а в отдельных случаях — единственным способом решить задачу[12].
На практике вместо генератора случайных чисел используют генератор псевдослучайных чисел.
Однако следует отличать стохастические алгоритмы и методы, которые дают с высокой вероятностью правильный результат. В отличие от метода, алгоритм даёт корректные результаты даже после продолжительной работы.
Некоторые исследователи допускают возможность того, что стохастический алгоритм даст с некоторой заранее известной вероятностью неправильный результат. Тогда стохастические алгоритмы можно разделить на два типа[14]:
- алгоритмы типа Лас-Вегас всегда дают корректный результат, но время их работы не определено.
- алгоритмы типа Монте-Карло, в отличие от предыдущих, могут давать неправильные результаты с известной вероятностью.
Другие формализации[править | править код]
Для некоторых задач названные выше формализации могут затруднять поиск решений и осуществление исследований. Для преодоления препятствий были разработаны как модификации «классических» схем, так и созданы новые модели алгоритма. В частности, можно назвать:
- многоленточная и недетерминированная машины Тьюринга;
- регистровая и РАМ-машина — прототип современных компьютеров и виртуальных машин;
- конечные и клеточные автоматы
Виды алгоритмов[править | править код]
Виды алгоритмов как логико-математических средств отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы в зависимости от цели, начальных условий задачи, путей её решения. Следует подчеркнуть принципиальную разницу между алгоритмами вычислительного характера, преобразующими некоторые входные данные в выходные (именно их формализацией являются упомянутые выше машины Тьюринга, Поста, РАМ, нормальные алгорифмы Маркова и рекурсивные функции), и интерактивными алгоритмами (уже у Тьюринга встречается C-машина, от англ. choice — выбор, ожидающая внешнего воздействия, в отличие от классической A-машины, где все начальные данные заданы до начала вычисления и выходные данные недоступны до окончания вычисления). Последние предназначены для взаимодействия с некоторым объектом управления и призваны обеспечить корректную выдачу управляющих воздействий в зависимости от складывающейся ситуации, отражаемой поступающими от объекта управления сигналами[15][16]. В некоторых случаях алгоритм управления вообще не предусматривает окончания работы (например, поддерживает бесконечный цикл ожидания событий, на которые выдается соответствующая реакция), несмотря на это, являясь полностью правильным.
Можно также выделить алгоритмы:
- Механические алгоритмы, или иначе детерминированные, жесткие (например, алгоритм работы машины, двигателя и т. п.) — задают определённые действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм.
- Гибкие алгоритмы, например, стохастические, то есть вероятностные и эвристические.
- Вероятностный (стохастический) алгоритм даёт программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.
- Эвристический алгоритм (от греческого слова «эврика») — алгоритм, использующий различные разумные соображения без строгих обоснований[17].
- Линейный алгоритм — набор команд (указаний), выполняемых последовательно во времени друг за другом.
- Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого может осуществляться разделение на несколько альтернативных ветвей алгоритма.
- Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций). К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы — последовательность команд (серия, тело цикла), которая может выполняться многократно.
- Вспомогательный (подчинённый) алгоритм (процедура) — алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм. На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.
- Структурная блок-схема, граф-схема алгоритма — графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков — графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия. Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, так как зрительное восприятие обычно облегчает процесс написания программы, её корректировки при возможных ошибках, осмысливание процесса обработки информации. Можно встретить даже такое утверждение: «Внешне алгоритм представляет собой схему — набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации».
Нумерация алгоритмов[править | править код]
Нумерация алгоритмов играет важную роль в их исследовании и анализе[18].
Поскольку любой алгоритм можно задать в виде конечного слова (представить в виде конечной последовательности символов некоторого алфавита), а множество всех конечных слов в конечном алфавите счётное, то множество всех алгоритмов также счётное. Это означает существование взаимно однозначного отображения между множеством натуральных чисел и множеством алгоритмов, то есть возможность присвоить каждому алгоритму номер.
Нумерация алгоритмов является одновременно и нумерацией всех алгоритмически исчисляемых функций, причем любая функция может иметь бесконечное количество номеров.
Существование нумерации позволяет работать с алгоритмами так же, как с числами. Особенно полезна нумерация в исследовании алгоритмов, работающих с другими алгоритмами.
Алгоритмически неразрешимые задачи[править | править код]
Формализация понятия алгоритма позволила исследовать существование задач, для которых не существует алгоритмов поиска решений. Впоследствии была доказана невозможность алгоритмического вычисления решений ряда задач, что делает невозможным их решение на любом вычислительном устройстве.
Функцию 


Случай, когда результатом вычисления функции 

Важно точно указывать допустимое множество входных данных, поскольку задача может быть решаемой для одного множества и нерешаемой для другого.
Одной из первых задач, для которой была доказана нерешаемость, является проблема остановки. Формулируется она следующим образом:
Имея описание программы для машины Тьюринга, требуется определить, завершит ли работу программа за конечное время или будет работать бесконечно, получив некоторые входные данные.[20]
Доказательство неразрешимости проблемы остановки важно тем, что к ней можно свести другие задачи. Например, простую проблему остановки можно свести к задаче остановки на пустой строке (когда нужно определить для заданной машины Тьюринга, остановится ли она, будучи запущенной на пустой строке), доказав тем самым неразрешимость последней.[19].
Анализ алгоритмов[править | править код]
Вместе с распространением информационных технологий увеличился риск программных сбоев. Одним из способов избежания ошибок в алгоритмах и их реализациях служат доказательства корректности систем математическими средствами.
Использование математического аппарата для анализа алгоритмов и их реализаций называют формальными методами. Формальные методы предусматривают применение формальных спецификаций и, обычно, набора инструментов для синтаксического анализа и доказательства свойств спецификаций. Абстрагирование от деталей реализации позволяет установить свойства системы независимо от её реализации. Кроме того, точность и однозначность математических утверждений позволяет избежать многозначности и неточности естественных языков[21].
По гипотезе Ричарда Мейса, «избежание ошибок лучше устранения ошибок»[22]. По гипотезе Хоара, «доказательство программ решает проблему корректности, документации и совместимости»[23]. Доказательство корректности программ позволяет выявлять их свойства по отношению ко всему диапазону входных данных. Для этого понятие корректности было разделено на два типа:
- Частичная корректность — программа даёт правильный результат для тех случаев, когда она завершается.
- Полная корректность — программа завершает работу и выдаёт правильный результат для всех элементов из диапазона входных данных.
Во время доказательства корректности сравнивают текст программы со спецификацией желаемого соотношения входных-выходных данных. Для доказательств типа Хоара спецификация имеет вид утверждений, которые называют предусловиями и постусловиями. В совокупности с самой программой их ещё называют тройкой Хоара. Эти утверждения записывают как
- {P}Q{S}
где P — это предусловия, должные выполняться перед запуском программы Q, а S — постусловия, истинные после завершения работы программы.
Формальные методы были успешно применены для широкого круга задач, в частности: разработке электронных схем, искусственного интеллекта, автоматических систем на железной дороге, верификации микропроцессоров, спецификации стандартов и спецификации и верификации программ[24].
Время работы[править | править код]

Распространённым критерием оценки алгоритмов является время работы и порядок роста продолжительности работы в зависимости от объёма входных данных.[25]
Для каждой конкретной задачи составляют некоторое число, которое называют её размером. Например, размером задачи вычисления произведения матриц может быть наибольший размер матриц-множителей, для задач на графах размером может быть количество ребер графа.
Время, которое тратит алгоритм как функция от размера задачи 

Асимптотическая сложность важна тем, что является характеристикой алгоритма, а не его конкретной реализации: «оптимизацией» операций, без замены алгоритма, можно изменить только мультипликативный коэффициент c, но не асимптотику. Как правило, именно асимптотическая сложность является главным фактором, который определяет размер задач, которые алгоритм способен обработать.
Часто во время разработки алгоритма пытаются уменьшить асимптотическую временную сложность для наихудших случаев. На практике же бывают случаи, когда достаточным является алгоритм, который «обычно» работает быстро.
Грубо говоря, анализ средней асимптотической временной сложности можно разделить на два типа: аналитический и статистический. Аналитический метод даёт более точные результаты, но сложен в использовании на практике. Зато статистический метод позволяет быстрее осуществлять анализ сложных задач[26].
В следующей таблице приведены распространённые асимптотические сложности с комментариями[27].
| Сложность | Комментарий | Примеры |
|---|---|---|
| O(1) | Устойчивое время работы не зависит от размера задачи | Ожидаемое время поиска в хеш-таблице |
| O(log log n) | Очень медленный рост необходимого времени | Ожидаемое время работы интерполирующего поиска n элементов |
| O(log n) | Логарифмический рост — удвоение размера задачи увеличивает время работы на постоянную величину | Вычисление xn; Двоичный поиск в массиве из n элементов |
| O(n) | Линейный рост — удвоение размера задачи удвоит и необходимое время | Сложение/вычитание чисел из n цифр; Линейный поиск в массиве из n элементов |
| O(n log n) | Линеаритмичный рост — удвоение размера задачи увеличит необходимое время чуть более, чем вдвое | Сортировка слиянием или кучей n элементов; нижняя граница сортировки сопоставлением n элементов |
| O(n²) | Квадратичный рост — удвоение размера задачи увеличивает необходимое время в четыре раза | Элементарные алгоритмы сортировки |
| O(n³) | Кубичный рост — удвоение размера задачи увеличивает необходимое время в восемь раз | Обычное умножение матриц |
| O(cn) | Экспоненциальный рост — увеличение размера задачи на 1 приводит к c-кратному увеличению необходимого времени; удвоение размера задачи увеличивает необходимое время в квадрат | Некоторые задачи коммивояжёра, алгоритмы поиска полным перебором |
Наличие исходных данных и некоторого результата[править | править код]
Алгоритм — это точно определённая инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.
Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так, алгоритм сложения применим к любой паре натуральных чисел. В этом выражается его свойство массовости, то есть возможности применять многократно один и тот же алгоритм для любой задачи одного класса.
Для разработки алгоритмов и программ используется алгоритмизация — процесс систематического составления алгоритмов для решения поставленных прикладных задач. Алгоритмизация считается обязательным этапом в процессе разработки программ и решении задач на ЭВМ. Именно для прикладных алгоритмов и программ принципиально важны детерминированность, результативность и массовость, а также правильность результатов решения поставленных задач.
Алгоритм — это понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение цели.
Представление алгоритмов[править | править код]
Формы записи алгоритма:
- словесная или вербальная: на естественном языке;
- на алгоритмическом языке: языке программирования или псевдокоде;
- в машинном коде (код процессора ЭВМ);
- в математической нотации (см. выше представленные варианты);
- схематическая:
- графическая (например, блок-схемы и ДРАКОН-схемы);
- структурограммы (диаграммы Насси-Шнейдермана).
Обычно сначала (на уровне идеи) алгоритм описывается словами, но по мере приближения к реализации он обретает всё более формальные очертания и формулировку на языке, понятном исполнителю (например, машинный код).
Эффективность алгоритмов[править | править код]
Хотя в определении алгоритма требуется лишь конечность числа шагов, требуемых для достижения результата, на практике выполнение огромного количество шагов приводит к длительному выполнению программ, также обычно есть другие ограничения (на размер программы, на допустимые действия). В связи с этим вводят такие понятия, как сложность алгоритма (временна́я, по размеру программы, вычислительная и другие).
Для каждой задачи может существовать множество алгоритмов, приводящих к цели. Увеличение эффективности алгоритмов составляет одну из задач информатики, начиная с 1940-х годов в связи с этим простроен ряд более эффективных в асимптотическом смысле алгоритмов для традиционных задач (например, алгоритмы быстрого умножения[en], алгоритм Чудновского для вычисления числа 
Пример[править | править код]
Алгоритм Евклида — эффективный метод вычисления наибольшего общего делителя (НОД). Назван в честь греческого математика Евклида; один из древнейших алгоритмов, который используют до сих пор[28].
Описан в «Началах» Евклида (примерно 300 лет до н. э.), а именно в книгах VII и X. В седьмой книге описан алгоритм для целых чисел, а в десятой — для длин отрезков.
Существует несколько вариантов алгоритма, ниже записанный в псевдокоде рекурсивный вариант:
алг нод(a, b)
нач
если b = 0
возврат a
иначе
возврат нод(b, a mod b)
кон

НОД чисел 1599 и 650:
| Шаг 1 | 1599 = 650*2 + 299 |
| Шаг 2 | 650 = 299*2 + 52 |
| Шаг 3 | 299 = 52*5 + 39 |
| Шаг 4 | 52 = 39*1 + 13 |
| Шаг 5 | 39 = 13*3 + 0 |
См. также[править | править код]
- Метаалгоритм
- Аукцион алгоритмов
- Список алгоритмов
- Теория алгоритмов
Примечания[править | править код]
- ↑ АЛГОРИ́ТМ : [арх. 30 октября 2018] / А. Л. Семёнов // А — Анкетирование. — М. : Большая российская энциклопедия, 2005. — С. 426. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 1). — ISBN 5-85270-329-X.
- ↑ Kleene 1943 in Davis 1965: 274
- ↑ Rosser 1939 in Davis 1965: 225
- ↑ Кнут, 2006, 1.1. Алгоритмы.
- ↑ Robert Andrew Wilson, Frank C. Keil. The MIT Encyclopedia of the Cognitive Sciences. — MIT Press, 2001. — С. 11. — 1106 с. — ISBN 9780262731447. Архивировано 17 ноября 2021 года.
- ↑ (Игошин, с. 317)
- ↑ В. А. Успенский: «Математика — это гуманитарная наука» // Троицкий вариант. — 2014. — 28 января (№ 2(146)). — С. 4—6. Архивировано 27 ноября 2018 года.
- ↑ Basics: The Turing Machine (with an interpreter!). Good Math, Bad Math (9 февраля 2007). Архивировано 11 февраля 2012 года.
- ↑ (Игошин, раздел 33)
- ↑ Энциклопедия кибернетики, т. 2, c. 90—91.
- ↑ (Игошин, раздел 34)
- ↑ 1 2 «Probabilistic algorithms should not be mistaken with methods (which I refuse to call algorithms), which produce a result which has a high probability of being correct. It is essential that an algorithm produces correct results (discounting human or computer errors), even if this happens after a very long time». Henri Cohen. A Course in Computational Algebraic Number Theory (англ.). — Springer-Verlag, 1996. — P. 2. — ISBN 3-540-55640-0.
- ↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rives’t, Clifford Stein. Introduction to Algorithms (англ.). — 2-е. — MIT Press, 2001. — P. 531. — ISBN 0-262-03293-7.
- ↑ (Раздел 12, с. 12—22 в Atallah, 2010)
- ↑ Dina Goldin, Peter Wegner. The origins of the Turing Thesis Myth, CS-04-14, October 2004
- ↑ Interactive Computation Is More Powerful Than Non Interactive. Архивировано 19 ноября 2015 года., c2.com
- ↑ М. Гэри, Д. Джонсон, Вычислительные машины и труднорешаемые задачи, М.: Мир, 1982, C. 155.
- ↑ (Игошин, раздел 36)
- ↑ 1 2 3 Peter Linz. An Introduction to Formal Languages and Automata (англ.). — Jones and Bartlett Publishers (англ.) (рус., 2000. — ISBN 0-7637-1422-4.
- ↑ computability and complexity, Encyclopedia of computer Science and Technology, Facts On File, 2009, ISBN 978-0-8160-6382-6.
- ↑ (O’Regan, раздел 4.5)
- ↑ (раздел 5.3.6 в Enders, 2003)
- ↑ (раздел 5.3.7 в Enders, 2003)
- ↑ (O’Regan, с. 119)
- ↑ А. Ахо, Дж. Хопкрофт, Дж. Ульман. Построение и анализ вычислительных алгоритмов = The Design and Analysis of Computer Algorithms. — М.: «Мир», 1979.
- ↑ (раздел 11 в Atallah, 2010)
- ↑ (раздел 1 в Atallah, 2010)
- ↑ Knuth D. The Art of Computer Programming, Volume 2: Seminumerical Algorithms (англ.). — 3rd. — Addison–Wesley, 1997. — ISBN 0201896842.
Литература[править | править код]
- Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms, Third Edition. — 3-е. — М.: «Вильямс», 2013. — 1328 с. — ISBN 978-5-8459-1794-2.
- Дональд Кнут. Искусство программирования = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд.. — М.: «Вильямс», 2006. — Т. 1. Основные алгоритмы. — С. 720. — ISBN 0-201-89683-4.
- Томас Х. Кормен. Алгоритмы: вводный курс = Algorithms Unlocked. — М.: «Вильямс», 2014. — 208 с. — ISBN 978-5-8459-1868-0.
- Игошин В. И. Математическая логика и теория алгоритмов. — 2-е изд., стер.. — М.: ИЦ «Академия», 2008. — 448 с. — ISBN 5-7695-1363-2.
Ссылки[править | править код]
- «Слово „алгоритм“: происхождение и развитие», В. В. Шилов, Журнал «Потенциал» — источник исторических сведений.
- Об алгоритме (недоступная ссылка — история). в энциклопедии «Кругосвет»
Алгоритмизация и
программирование
Введение
Каждый из нас постоянно
решает множество задач: как быстрее собраться на работу, как лучше спланировать
дела текущего дня и многие другие. Некоторые задачи мы решаем автоматически,
так как на протяжении многих лет привыкли к их выполнению, другие требуют
длительного размышления над решением, но в любом случае, решение каждой задачи
всегда делится на простые действия.
Алгоритмизация– это техника
разработки алгоритма для решения задач на компьютере. Изобразительные средства
для представления или описания алгоритма.
Понятие алгоритма,
являющееся фундаментальным в математике и информатике, возникло задолго до
появления средств вычислительной техники. Слово «алгоритм» появилось в средние
века, когда европейцы познакомились со способами выполнения арифметических
действий в десятичной системе счисления, описанными узбекским математиком
Муххамедом бен Аль-Хорезми («аль-Хорезми» — человек из города Хорезми); в
настоящее время город Хива в Хорезмской области Узбекистана). Слово алгоритм –
есть результат европейского произношения слов аль-Хорезми.
Первоначально под
алгоритмом понимали способ выполнения арифметических действий над десятичными
числами. В дальнейшем это понятие стали использовать для обозначения любой
последовательности действий, приводящей к решению поставленной задачи.
Чтобы решать задачи на
компьютере, необходимо владеть языком программирования, обладать знаниями в
области информационного моделирования и алгоритмизации.
Этапы
решения задачи на компьютере
На первом этапе обычно осуществляется
постановка задачи, происходит осознание её условия. При этом должно быть чётко
определено, что дано, какие исходные данные известны, какие являются
параметрами к условию задачи, и что требуется найти в решаемой задаче. Также
должны быть чётко выделены существенные свойства рассматриваемого объекта, указаны
связи между исходными данными и результатами.
На втором этапе описательная информационная модель
формализуется, т.е записывается с помощью некоторого формального языка.
В свою очередь этапы чётко зависят от полученного результата:
Этап = Результат
Поставка задачи Словесная
информационная модель
Формализация Математическая
модель
Алгоритмизация Алгоритм
Программирование Программа
Отладка, тестирование Уточнённая
модель
Выполнение расчётов Ответы на поставленные в задаче
вопросы
Для правильной установки этапов, требуется:
·
понять, к какому классу
принадлежит рассматриваемая задача;
·
записать известные связи
между исходными данными и результатами с помощью математических соотношений;
·
выбрать наиболее
подходящий способ для решения задачи.
На третьем этапе
осуществляется построение алгоритма – чёткой инструкции, задающей необходимую
последовательность действий для решения задачи. Алгоритм чаще всего
представляется в форме блок-схемы ввиду её наглядности и универсальности.
На четвёртом этапе алгоритм записывается
на одном из языков программирования. Важно отметить, что основной ошибкой
многих пользователей компьютером, является мнение о том, что HTML – это язык программирования. На самом деле HTML – это
язык разметки.
На пятом этапе осуществляется отладка и
тестирование программы.
Отладка программы – это процесс проверки
работоспособности программы и исправления обнаруженных при этом ошибок.
Ошибки могут быть связаны с нарушением правил
записи программы на конкретном языке программирования, таким образом, на Pascal’e используется
в качестве ввода информации на экран команда “write/writeln”,
когда в это же время, на C эта же команда обозначается с помощью “printf”.
На шестом этапе по уточнённой программе
проводятся необходимые вычисления, результаты которых позволяют ответить на
поставленные в задаче вопросы.
Рассмотренные этапы являются основой разработки, и
написания программного обеспечения, но при этом называются они несколько иначе.

![]()
![]()

![]()
![]()
![]()

![]()
![]() Этапы разработки программного обеспечения:
Этапы разработки программного обеспечения:
На этапе подготовки разработчик уточняет у
заказчика требования к программному продукту, осуществляет предварительное
планирование этапов работ, сроков, ресурсов и стоимости разработки.
На этапе проектирования составляется требования к
программе, определяются её технические характеристики, выбираются алгоритмы
реализации программы.
На этапе создания происходит разработка
интерфейса программы (кнопки, иконки, расположение и т.д); создается
программный код – пишется программа, реализующая ранее выбранный алгоритм; осуществляются
отладка и тестирование программы. На этом же этапе создается пакет документации,
включающий различные описания, инструкции и руководства. Наличие подробной
документации обеспечивает в том числе возможность передачи накопленных знаний
другим разработчикам.
На этапе поддержки происходит установка
разработанного программного обеспечения (внедрение), исправление выявленных
ошибок и поддержка пользователей (сопровождение).
Задачи
Разберем
последовательность этапов решения задач на компьютере, на таких языках
программирования как Pascal и C.
Начнем пожалуй,
с C:
Напишите
программу, которая высчитывает плату за пользование кредитом после того как
введены сумма кредита, процентная годовая ставка и срок кредита в днях = сумма
* процентная ставка * (срок кредита в днях / 365)
Первый этап.
Дано:
Параметры – сумма кредита; процентная
годовая ставка; срок кредита в днях;
Срок кредита в днях – Сумма кредита * Процентная
годовая ставка * (Срок кредита в днях / 365).
Где * — умножение, а / — деление.
Требуется найти: Плату за пользование кредитом.
Второй этап.
В данной ситуации мы имеет дело с формулой, по которой мы должны
рассчитать поставленное нам условие в задаче, а именно:
Срок кредита в днях – Сумма кредита *
Процентная годовая ставка * (Срок кредита в днях / 365).
Третий этап.
В данном этапе представим алгоритм решения
задачи в виде блок-схемы:
 |
|||||||||||
 |
|||||||||||
 |
|||||||||||
 |
Четвёртый этап.
Запишем данный алгоритм на языке программирования C в программе
“Microsoft Visual Studio”.
#include <stdio.h>
int main() {
float Sum, PY, DateOfCredit;
printf(«Enter the amount of you credit =
n»);
// введите сумму кредита
scanf_s(«%f», &Sum);
printf(«Enter the annual interest rate =
n»);
// введите процентную годовую ставку
scanf_s(«%f», &PY);
printf(«Enter the date of you credit =
n»);
// введите срок кредита
scanf_s(«%f», &DateOfCredit);
printf(«Your charge is = %1f», Sum * PY *
(DateOfCredit / 365));
return 0;
}
Пятый этап.
Протестировать составленную программу можно, используя информацию, которую
вводит пользователь в поле для ввода данных.
Шестой этап
Выполнив программу несколько раз при различных исходных данных, можно
сделать вывод: чем больше числа, которые вводит пользователь, тем больше плата
за использование кредита.
Следующая программа будет написана на Pascal:
Водитель
автомобиля, движущегося с некоторой постоянной скоростью, увидев красный свет
светофора, нажал на тормоз. После этого скорость автомобиля стала уменьшаться
каждую секунду на 5 метров. Требуется найти расстояние, которое автомобиль
пройдет до полной остановки.
Первый этап.
Дано:
![]() –
–
начальная скорость;
![]() –
–
конечная скорость (равно нулю, так как автомобиль остановился);
![]() –
–
ускорение (равно -5м/c²).
Требуется найти: ![]() – расстояние, которое автомобиль пройдёт до
– расстояние, которое автомобиль пройдёт до
полной остановки.
Второй этап.
В данной ситуации мы имеем дело с прямолинейным равноускоренным движением
тела. Формула для перемещения при этом имеет вид:
![]()
Упрости эту формулу с учётом того, что конечная
скорость равна нулю: ![]() . При
. При
![]() =
=
5м/c² получим: ![]() (при
(при
условии задания скорости в метрах в секунду и вычислении пути в метрах).
Третий этап.
![]()
![]()
![]()
![]()




 Представим алгоритм решения задачи в виде блок-схемы:
Представим алгоритм решения задачи в виде блок-схемы:
Четвертый этап.
Запишем данный алгоритм на языке программирования Паскаль:
program
n_1;
var
v0, s: real;
begin
writeln(‘Вычисление длины пути торможения автомобиля’);
write(‘Введите начальную скорость (м/c)>>’);
readln (v0);
s:=v0*v0/10;
writeln(‘До полной остановки автомобиль пройдет — ‘, s:8:4, ‘
м. ’)
end.
Пятый этап.
Протестировать составленную программу можно, используя информацию, что
при скорости 72км/ч с начала торможения до полной остановки автомобиль проходит
40 метров.
Шестой этап.
Выполнив программу несколько раз при различных исходных данных, можно
сделать вывод: чем больше начальная скорость автомобиля, тем большее расстояние
он пройдет с начала торможения до полной остановки.
Применяя компьютер для решения задач, всегда следует
помнить, что наряду с огромным быстродействием и абсолютной исполнительностью у
компьютера отсутствуют интуиция и чувство здравого смысла и он способен решать
только ту задачу, программу решения которой ему подготовил человек.
Источники
Учебник Л.Л.Босова
и А.Ю.Босова — Информатика 9 класс (дата обращения: 19.10.2020)
Россия // Учебник Л.Л.Босова и А.Ю.Босова [2020]. Дата обновления: 15.10.2020.
URL: https://moodle.kstu.ru/mod/page/view.php?id=47344 (дата
обращения: 19.10.2020).
Россия // Deitel C —
Задачи — Глава 3 [2020]. Дата обновления: 18.10.2020.
URL: http://isec.nayanovaacademy.ru/wiki/Deitel_C_-_Задачи_-_Глава_3#03.19 (дата
обращения: 19.10.2020).
Конспект урока Программирование как этап решения задачи на компьютере (9 класс, урок 36, учебник Босова Л.Л.). На уроке учащиеся знакомятся с этапами решения задачи на компьютере.
Планируемые образовательные результаты:
— предметные – представление об основных этапах решения задачи на компьютере;
— метапредметные – умение самостоятельно планировать пути достижения целей; умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности, определять способы действий в рамках предложенных условий, корректировать свои действия в соответствии с изменяющейся ситуацией; умение оценивать правильность выполнения учебной задачи; владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;
— личностные – алгоритмическое мышление, необходимое для профессиональной деятельности в современном обществе; представление о программировании как сфере возможной профессиональной деятельности.
Решаемые учебные задачи:
1) познакомить учащихся с этапами решения задачи на компьютере;
2) продемонстрировать все этапы решения задачи на компьютере на примере задачи о пути торможения автомобиля.
Основные понятия, изучаемые на уроке:
— постановка задачи;
— формализация;
— алгоритмизация;
— программирование;
— отладка и тестирование.
Используемые на уроке средства ИКТ:
— персональный компьютер (ПК) учителя, мультимедийный проектор, экран;
— ПК учащихся.
Электронные образовательные ресурсы
— презентация «Программирование как этап решения задачи на компьютере».
Особенности изложения содержания темы урока
1. Организационный момент (1 минута)
Приветствие учащихся, сообщение темы и целей урока.
2. Повторение (4 минуты)
1) проверка изученного материала по вопросам (1-10) к §4.2;
2) визуальная проверка выполнения домашнего задания в РТ № 176-179;
3) рассмотрение заданий, вызвавших затруднения при выполнении домашнего задания
3. Изучение нового материала (20 минут)
Новый материал излагается в сопровождении презентации «Программирование как этап решения задачи на компьютере».
1 слайд — название презентации;
2 слайд — ключевые слова;
— постановка задачи
— формализация
— алгоритмизация
— программирование
— отладка и тестирование
3 слайд — этапы решения задач на компьютере (схема);
Компьютерные программы программисты создают для решения разнообразных задач. Программирование — важный, но не единственный этап решения задачи на компьютере.
На первом этапе обычно строится словесная информационная модель объекта или процесса. При этом должно быть четко определено, что дано (какие исходные данные известны, какие данные допустимы) и что требуется найти в решаемой задаче. Также должны быть четко выделены наиболее существенные свойства рассматриваемого объекта, указаны связи между исходными данными и результатами.
На втором этапе описательная информационная модель формализуется, т. е. записывается с помощью некоторого формального языка. Для этого требуется:
— понять, к какому классу принадлежит рассматриваемая задача;
— записать известные связи между исходными данными и результатами с помощью математических соотношений;
— выбрать наиболее подходящий способ для решения задачи.
На третьем этапе осуществляется построение алгоритма — чёткой инструкции, задающей необходимую последовательность действий для решения задачи. Алгоритм чаще всего представляется в форме блок-схемы, ввиду её наглядности и универсальности.
На четвёртом этапе алгоритм записывается на одном из языков программирования. Вы учитесь записывать программы на языке Паскаль.
На пятом этапе осуществляется отладка и тестирование программы. Этап отладки и тестирования так лее называют компьютерным экспериментом.
Отладка программы — это процесс проверки работоспособности программы и исправления обнаруженных при этом ошибок. Ошибки могут быть связаны с нарушением правил записи программы на конкретном языке программирования. Их программисту помогает выявить используемая система программирования; она выдаёт на экран сообщения о выявленных ошибках.
Проверка правильности разработанной программы осуществляется с помощью тестов. Тест — это конкретный вариант значений исходных данных, для которого известен ожидаемый результат.
4 слайд — задача о пути торможения автомобиля;
Рассмотрим последовательность прохождения этапов решения задачи на компьютере на примере простой задачи.
Водитель автомобиля, движущегося с некоторой постоянной скоростью, увидев красный свет светофора, нажал на тормоз. После этого скорость автомобиля стала уменьшаться каждую секунду на 5 метров. Требуется найти расстояние, которое автомобиль пройдёт до полной остановки.
Первый этап.
Дано:
V0х — начальная скорость;
Vx — конечная скорость (равна нулю, так как автомобиль остановился);
ах — ускорение (равно -5 м/с).
Требуется найти: sx — расстояние, которое автомобиль пройдёт до полной остановки.
5 слайд — задача о пути торможения автомобиля;
Второй этап.
В данной ситуации мы имеем дело с прямолинейным равноускоренным движением тела. Формула для перемещения при этом имеет вид:

Упростим эту формулу с учётом того, что конечная скорость равна нулю:

При ax= — 5м/с получим:

6 слайд — задача о пути торможения автомобиля;
Третий этап.
Представим алгоритм решения задачи в виде блок-схемы:

7 слайд — задача о пути торможения автомобиля;
Четвёртый этап.
Запишем данный алгоритм на языке программирования Паскаль:
program n_2;
var v0, s: real;
begin
writeln (‘Вычисление длины пути торможения автомобиля’);
write (‘Введите начальную скорость (м/с)> ‘);
readln (v0);
s:=v0*v0/10;
writeln (‘До полной остановки автомобиль пройдет’, s:8:4,’ м.’)
end.
8 слайд — задача о пути торможения автомобиля;
Пятый этап.
Протестировать составленную программу можно, используя ту информацию, что при скорости 72 км/ч с начала торможения до полной остановки автомобиль проходит 40 метров.
Выполнив программу несколько раз при различных исходных данных, можно сделать вывод: чем больше начальная скорость автомобиля, тем большее расстояние он пройдет с начала торможения до полной остановки.
Применяя компьютер для решения задач, всегда следует помнить, что наряду с огромным быстродействием и абсолютной исполнительностью у компьютера отсутствуют интуиция и чувство здравого смысла, и он способен решать только ту задачу, программу решения которой ему подготовил человек.
9 слайд — самое главное.
— Этапы решения задачи с использованием компьютера:
1) постановка задачи;
2) формализация;
3) алгоритмизация;
4) программирование;
5) компьютерный эксперимент.
— Для решения задач на компьютере необходимо владеть языком программирования, обладать знаниями в области информационного моделирования и алгоритмизации.
Вопросы и задания
10 слайд – вопросы и задания;
Вопросы 1-12 к параграфу 4.3
4. Практическая часть (15 минут)
Рассмотреть задачи №11 и №12 из учебника и №180 из рабочей тетради (выполнить все 5 этапов).
Рассмотрение каждой задачи завершить выполнением программы на компьютере в среде программирования PascalABC.NET. Скачать ее можно по ссылке на сайте (https://pascalabc.net/).
Задание 1. Уличный продавец газет получает а рублей с продажи каждой из первых 50 газет. С продажи каждой из остальных газет он получает на 20% больше.
Разработайте программу, которая вычислит заработок продавца, если он продаст за день 200 газет. Зафиксируйте свои действия на каждом из этапов решения этой задачи (задание №11 в учебнике).
Задание 2. В аэробусе, вмещающем 160 пассажиров, три четверти мест находятся в салонах экономического класса и одна четверть мест — в салоне бизнес-класса. Стоимость билета в салоне бизнес класса составляет х рублей, что в два раза выше стоимости билета в салонах экономического класса.
Разработайте программу, которая вычислит сумму денег, полученную авиакомпанией от продажи билетов на этот рейс, если известно, что остались нераспроданными а билетов бизнес-класса и b билетов экономического класса. Выделите все этапы решения этой задачи и опишите свои действия на каждом из них (задание №12 в учебнике).
Задание 3. В первый час работы рабочий изготавливает а деталей, за каждый последующий час — на d деталей больше, чем за предыдущий.
Разработайте программу, которая подсчитает, сколько деталей изготовил рабочий за 8 часов работы (задание №180 в РТ).
5. Подведение итогов урока. Сообщение домашнего задания. Выставление оценок (4 минуты)
11 слайд — опорный конспект;
12 слайд — Д/з.
Домашнее задание.
§4.3, вопросы № 1-12 к параграфу;
РТ: № 180.
Весь материал к уроку находится в архиве.
Скачать (599 КБ, rar): Конспект урока Программирование как этап решения задачи на компьютере 9 класс
Архив включает в себя:
— конспект,
— ответы и решения на задания в учебнике и в рабочей тетради,
— презентация «Программирование как этап решения задачи на компьютере».



