Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Теорема
a = b · q + r, где a — делимое, b — делитель, q — неполное частное, r — остаток. 0 ⩽ r < |b|.
Предложите ребёнку поиграть в математику
Бесплатный математический комикс с творческими задачами на логику и сообразительность

Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
- 7 * 2 + 1 = 15;
- 2 * 7 + 1 = 15.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Самый удобный способ деления — это столбик.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Как решаем:
Выполним деление столбиком:
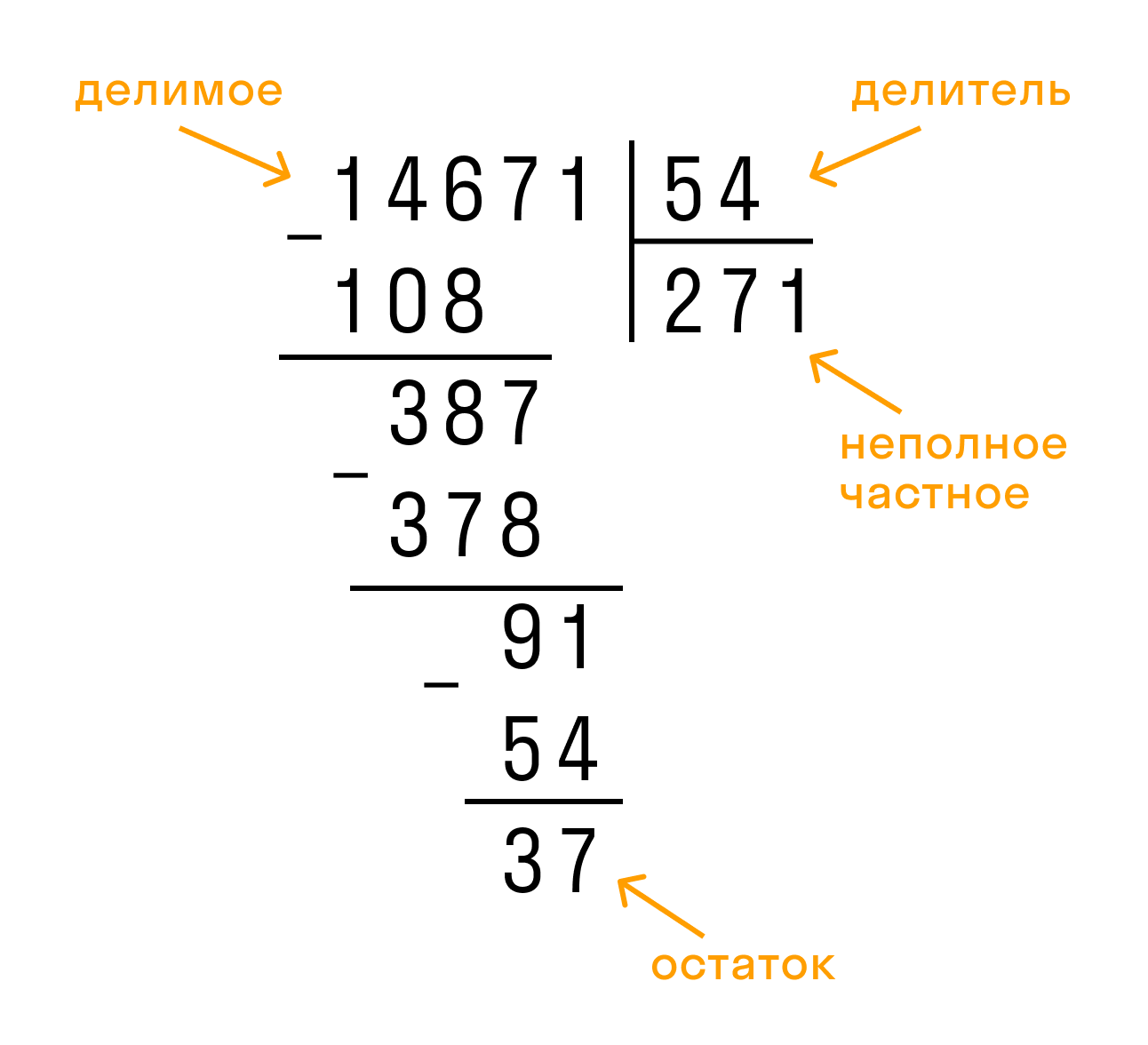
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Выберите идеального репетитора по математике
15 000+ проверенных преподавателей со средним рейтингом 4,8. Учтём ваш график и цель обучения

Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя
- получить неполное частное и остаток;
- записать число противоположное полученному.
Пример
Разделить 17 на −5 с остатком.
Как решаем:
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Проверка : a = b * q + r, 17 = −5 * (−3) + 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное q при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток r будет вычисляться по формуле:
r = a − b * q
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
- найти модули делимого и делителя;
- разделить по модулю;
- записать противоположное данному число и вычесть 1;
- использовать формулу для остатка r = a − b * q.
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Как решаем:
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, q = −4, тогда:
r = a − b * q = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Проверка: a = b * q + r, −17 = 5 * (−4) + 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
r = a − b * q
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя;
- получить неполное частное и остаток;
- прибавить 1 к неполному частному;
- вычислить остаток, исходя из формулы r = a − b * q.
Пример
Найти неполное частное и остаток при делении −17 на −5.
Как решаем:
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим r = a − b * q = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Проверка: a = b * q + r, −17 = −5 * 4 + 3.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.

Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.

Решение: 11 : 3 = 3 (остаток 2).
Эта статья — об алгоритмах деления целых чисел. О делении столбиком см. Деление столбиком; о теореме существования единственного частного и остатка см. Деление с остатком; о делении многочленов см. Деление многочленов.
Алгоритм деления — это алгоритм, вычисляющий для двух данных целых чисел 

Алгоритмы деления разбиваются на две большие категории: медленное деление и быстрое деление. Алгоритмы медленного деления дают по одному знаку результата за итерацию. Примерами медленного деления служат алгоритмы деления с восстановлением, без восстановления и SRT. Методы быстрого деления начинаются с аппроксимации конечного частного и дают вдвое больше знаков в конечном результате на каждой итерации. Алгоритмы Ньютона – Рапсона и Гольдшмидта попадают в эту категорию.
Варианты этих алгоритмов позволяют использовать быстрые алгоритмы умножения. В результате этого для больших целых чисел время вычисления, необходимое для деления, будет тем же самым (с точностью до постоянного множителя), что и время, необходимое для выполнения умножения, какой бы алгоритм из перечисленных не был применён.
Обсуждение будет использовать обозначения 
являются входными числами, а
являются выходными данными.
Деление путём вычитаний[править | править код]
Простейший алгоритм, исторически встроенный в алгоритм поиска наибольшего общего делителя и представленный в Началах Евклида, Книга VII Предложение 1, находит остаток деления двух положительных целых чисел с помощью только вычитания и сравнения:
R := N while R >= D do R := R − D end return R
Доказательство, что частное и остаток существуют и единственные (описано в статье Деление с остатком) дают полный алгоритм деления, основанный на сложениях, вычитаниях и сравнениях:
function divide(N, D) if D = 0 then error(DivisionByZero) end if D < 0 then (Q, R) := divide(N, −D); return (−Q, R) end if N < 0 then (Q,R) := divide(−N, D) if R = 0 then return (−Q, 0) else return (−Q − 1, D − R) end end -- Здесь N >= 0 и D >= 0 return divide_unsigned(N, D) end function divide_unsigned(N, D) Q := 0; R := N while R >= D do Q := Q + 1 R := R − D end return (Q, R) end
Эта процедура всегда даёт 


Деление столбиком[править | править код]
Деление столбиком является стандартным алгоритмом многозначных чисел в десятичной системе счисления, используемых для деления с помощью карандаша и бумаги. Он сдвигается постепенно слева направо от делимого, вычитая наибольшее возможное кратное делителя на каждом шаге. Множитель становится цифрой в частном, а конечная разность становится остатком от деления.
Когда алгоритм используется по основанию 2, этот метод образует базис для деления натуральных чисел с остатком. Короткое деление[en] является вариантом деления в столбик, пригодным для деления на одну цифру. Алгоритм уменьшения[en], известный также как метод неполных частных, является менее эффективным видом деления столбиком, но который проще понять. Разрешение вычитать большее кратное число, чем делается на каждом шаге, даёт больше свободы для создания вариантов деления в столбик.
Деление целых чисел (без знака) с остатком[править | править код]
Приведённый алгоритм, двоичная версия известного деления в столбик, делит 



if D = 0 then error(DivisionByZeroException) end -- Деление на ноль Q := 0 -- Начальные значения частного и остатка полагаем равны 0 R := 0 for i := n − 1 .. 0 do -- Здесь n равно числу бит в N R := R << 1 -- Сдвиг влево числа R на 1 бит R(0) := N(i) -- Полагаем младший бит R равным биту i делимого if R >= D then R := R − D Q(i) := 1 end end
Пример[править | править код]
Возьмём 



Шаг 1: Set R = 0 and Q = 0
Шаг 2: Take i = 3 (на единицу меньше числа бит в N)
Шаг 3: R = 00 (сдвиг влево на 1)
Шаг 4: R = 01 (полагаем R(0) равным N(i))
Шаг 5: R < D, так что пропускаем команду
Шаг 2: Set i = 2
Шаг 3: R = 010
Шаг 4: R = 011
Шаг 5: R < D, пропускаем команду
Шаг 2: Set i = 1
Шаг 3: R = 0110
Шаг 4: R = 0110
Шаг 5: R >= D, команда выполняется
Шаг 5b: R = 10 (R−D)
Шаг 5c: Q = 10 (полагаем Q(i) равным 1)
Шаг 2: Set i = 0
Шаг 3: R = 100
Шаг 4: R = 100
Шаг 5: R >= D, команда выполняется
Шаг 5b: R = 0 (R−D)
Шаг 5c: Q = 11 (полагаем Q(i) равным 1)
Конец



Методы медленного деления[править | править код]
Все методы медленного деления основываются на стандартном рекуррентном отношении[1]
где:
Восстанавливающее деление[править | править код]
Восстанавливающее деление работает с дробными числами числами с плавающей запятой и зависит от предположения 
Цифры частного 

Основной восстанавливающий алгоритм для двоичного (по основанию 2):
R := N D := D << n -- R и D должны быть словами вдвое длиннее, чем N и Q for i := n − 1 .. 0 do -- Например, 31..0 для 32 бит R := 2 * R − D -- Пробное вычитание из сдвинутого значения (умножение на 2 есть сдвиг в бинарной интерпретации) if R >= 0 then q(i) := 1 -- Результат - бит 1 else q(i) := 0 -- Результат - бит 0 R := R + D -- Новый частичный остаток равен (восстановленному) сдвинутому значению end end -- Здесь: N = делимое, D = делитель, n = число бит, R = частичный остаток, q(i) = бит № i частного
Вариант алгоритма, не осуществляющий явно 


Невосстанавливающее деление[править | править код]
Невосстанавливающее деление использует набор цифр 

R := N D := D << n -- R и D должны быть словами вдвое длиннее, чем N и Q for i = n − 1 .. 0 do -- Например, 31..0 для 32 бит if R >= 0 then q[i] := +1 R := 2 * R − D else q[i] := −1 R := 2 * R + D end if end -- Здесь: N = делимое, D = делитель, n = число бит, R = частичный остаток, q(i) = бит №i частного.
Если следовать этому алгоритму, получаем частное в нестандартном формате, состоящем из цифр -1 и +1. Этот вид нужно преобразовывать в двоичную форму. Пример:
Преобразование частного к цифрам  : :
|
|
| Старт: | 
|
| 1. Образуем положительный член: | 
|
| 2. Образуем отрицательный член: | 
|
3. Вычитаем:  : : |

|
| Отрицательный член представлен в бинарном обратном коде, не в дополнительном коде |
Если −1 знаки 




Q := Q − bit.bnot(Q) -- Если цифры −1 в Q представлены как нули.
Наконец, частные, вычисляемые этим алгоритмом, всегда нечётные, а остаток R находится в пределах 


if R < 0 then Q := Q − 1 R := R + D end if
Истинный остаток равен R >> n. Как и в варианте с восстановлением, младшие биты 

Деление SRT[править | править код]
Деление названо по первым буквам фамилий создателей (Sweeney, Robertson, Tocher). Деление SRT является популярным методом деления во многих микропроцессорах[3][4]. Деление подобно делению без восстановления, но использует таблицу поиска на основе делимого и делителя для определения цифры частного.
Наиболее существенная разница в том, что используется избыточное представление для частного. Например, если реализуется деление SRT по основанию 4, каждая цифра частного выбирается из пяти возможностей: 



Подобно невосстанавливающему делению конечными шагами являются вычитание по полной длине чисел, чтобы получить последний бит частного, и приведение частного к стандартному двоичному виду.
Печально известный баг плавающего деления в процессорах Intel Pentium был вызван неправильно закодированной таблицей поиска. Пять из 1066 ячеек таблицы были ошибочно опущены[5][6].
Методы быстрого деления[править | править код]
Деление Ньютона – Рапсона[править | править код]
Деление Ньютона – Рапсона использует метод Ньютона для нахождения обратного к 


Шаги деления Ньютона – Рапсона:
- Вычисляем приближение
для обратного числа
делителя
.
- Последовательно вычисляем более точные приближения
обратного числа. Это место, где, собственно, и используется метод Ньютона – Рапсона.
- Вычисляем частное путём умножения делимого на обратное к делителю:
.
Чтобы применить метод Ньютона для нахождения обратного к 





что можно вычислить из 
С точки зрения вычислений выражения 







Если ошибка определяется как 
Эта ошибка в квадрате на каждом шаге итерации (так называемая квадратичная сходимость метода Ньютона – Рапсона) имеет эффект такой, что число верных знаков в результате, грубо говоря, удваивается для каждой итерации, свойство, которое становится крайне важным, когда встречающиеся числа имеют много знаков. Но это также означает, что начальная сходимость метода может оказаться сравнительно медленной, особенно если значение 
Для подзадачи выбора начальной оценки 



для инициализации метода Ньютона – Рапсона. Чтобы минимизировать максимальную абсолютную ошибку этого приближения на интервале ![{displaystyle [0{,}5,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ee044e15086e4d3cb6889af6dcd8692c9e2690)
Коэффициенты линейного приближения определяются следующим образом. Абсолютное значение ошибки равно 








Можно образовать многочлен со степенью большей 1, вычислив коэффициенты согласно алгоритму Ремеза. Тогда начальное приближение требует больших вычислений, что может компенсироваться меньшим числом итерация Ньютона – Рапсона.
Поскольку сходимость этого метода в точности квадратичная, отсюда следует, что достаточно
шагов для вычисления значения с точностью до 
Псевдокод[править | править код]
Следующий псевдокод вычисляет частное от деления N и D с точностью до P двоичных знаков:
Выражаем D как, где
(стандартное представление с плавающей запятой)
// приводим к значению между 0,5 и 1, что можно выполнить битовым сдвигом / вычитанием экспоненты

// заранее вычисленные константы с той же точностью, что и D повторить
раз // может быть вычислено заранее для фиксированного P
конец возвратить

Например, для деления двойной точности с плавающей запятой этот метод использует 10 умножений, 9 сложений и 2 сдвига.
Варианты деления Ньютона – Рапсона[править | править код]
Метод деления Ньютона – Рапсона можно модифицировать, чтобы сделать чуть быстрее. После сдвига N и D, так что D будет в интервале [0,5, 1,0], инициализируем с
.
Это лучшее квадратичное приближение к 

Тогда в цикле используем итерацию, которая возводит ошибку в куб.
Если цикл выполняется пока 


что равно числу раз возведения 99 в куб, чтобы получить 
равно частному с точностью до 
Использование многочленов более высокой степени при инициализации или итерациях приводит к падению производительности, поскольку дополнительные умножения лучше было бы использовать для совершения большего числа итераций.
Деление Гольдшмидта[править | править код]
Деление Гольдшмидта[7] (Robert Elliott Goldschmidt) использует итеративный процесс многократного умножения делимого и делителя на один и тот же множитель 

Шаги деления Гольдшмидта:
- Генерируем приближение для множителя
.
- Умножаем делимое и делитель на
.
- Если делитель достаточно близок к 1, возвращаем делимое, в противном случае возвращаемся к шагу 1.
Предполагаем, что 



Умножаем делимое и делитель на множитель и получаем:
После достаточного числа 

Метод Гольдшмидта используется в процессорах AMD Athlon и более поздних моделях[8][9]. Он известен также как Anderson Earle Goldschmidt Powers (AEGP) алгоритм и реализован в различных процессорах IBM[10][11]. Хотя сходимость метода такая же, как у реализации Ньютона – Рапмона, одно из преимуществ метода Гольдшмидта в том, что умножения в числителе и знаменателе можно делать параллельно[11].
Биномиальная теорема[править | править код]
Метод Гольдшмидта можно использовать с множителями, которые позволяют упрощение с помощью бинома Ньютона.
Предположим, что N/D умножено на степень двойки так, что ![{displaystyle Din ({tfrac {1}{2}},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7160daabbf819632931c585f684e33cdc382eae9)
Мы выбираем 

Это даёт
.
После 



,
которая имеет максимальную величину 


Методы для больших чисел[править | править код]
Методы, предназначенные для аппаратной реализации, обычно не рассчитаны на целые числа с тысячами или миллионами десятичных цифр, что часто встречается, например, при вычислениях по сравнению по модулю в криптографии. Для этих больших чисел более эффективные алгоритмы преобразуют задачу к использованию малого числа умножений, которые можно сделать с помощью асимптотически эффективных алгоритмов умножения[en], таких как Алгоритм Карацубы, умножение Тума – Кука[en], или алгоритм Шёнхаге — Штрассена. В результате вычислительная сложность деления будет того же порядка (с точностью до умножения на константу) как и умножения. Примеры включают сведение к умножению по методу Ньютона как описанное выше[12], так и чуть более быстрое деление Бурникеля – Циглера[13], алгоритмы Барета[en] и Монтгомери[14]. Метод Ньютона, в частности, эффективен в сценариях, где нужно делить на определённое число несколько раз, поскольку после начального нахождения обратного значения только одно (сокращённое) умножение нужно для каждого умножения.
Деление на константу[править | править код]
Деление на константу 
Поскольку знаменатель постоянен, постоянна и обратная величина 





Нет необходимости использовать именно 










Однако, если 






В качестве конкретного примера арифметики с фиксированной запятой, для 32-битных беззнаковых целых, деление на 3 может быть заменено на умножение на 


Для общего деления 






где 
В некоторых случаев деление на константу может быть совершено даже за меньшее время путём замены «умножения на константу» в серию сдвигов и сложений или вычитаний[20]. Особый интерес представляет деление на 10, для которого получается точное частное с остатком, если потребуется[21].
См. также[править | править код]
- Метод галеры
- Длинная арифметика — Алгоритмы деления
- Ошибка Pentium FDIV
Примечания[править | править код]
- ↑ Несмотря на то, как «мала» проблема, вызываемая оптимизацией, эта оптимизация обычно спрятана за флаг «быстрая математика» в современных компиляторах.
- ↑ Современные Компиляторы обычно осуществляют эту оптимизацию целого умножения-и-сдвига. Для констант, известных только в момент выполнения программа должна реализовать оптимизацию сама[18]
- ↑ Morris, Iniewski, 2017.
- ↑ Flynn Stanford EE486 (Advanced Computer Arithmetic Division) – Chapter 5 Handout (Division). Stanford University. Дата обращения: 10 января 2022. Архивировано 18 апреля 2022 года.
- ↑ Harris, Oberman, Horowitz, 1998.
- ↑ McCann, Pippenger, 2005, с. 1279–1301.
- ↑ Statistical Analysis of Floating Point Flaw. Intel Corporation (1994). Дата обращения: 22 октября 2013. Архивировано 23 октября 2013 года.
- ↑ Oberman, Flynn, 1995.
- ↑ Goldschmidt, 1964.
- ↑ Oberman, 1999, с. 106-115.
- ↑ Soderquist, Leeser, 1997, с. 56-66.
- ↑ Anderson, Earle, Goldschmidt, Powers, 1997.
- ↑ 1 2 Guy, Peter, Ferguson, 2005, с. 118–139.
- ↑ Hasselström, 2003.
- ↑ Burnikel, Ziegler, 1998.
- ↑ Barrett, 1987, с. 311-323.
- ↑ Granlund, Montgomery, 1994, с. 61–72.
- ↑ Möller, Granlund, 2011, с. 165–175.
- ↑ ridiculous_fish.
«Labor of Division (Episode III): Faster Unsigned Division by Constants» Архивная копия от 8 января 2022 на Wayback Machine.
2011. - ↑ ridiculous_fish libdivide, optimized integer division. Дата обращения: 6 июля 2021. Архивировано 23 ноября 2021 года.
- ↑ Warren Jr., 2013, с. 230-234.
- ↑ LaBudde, Robert A.; Golovchenko, Nikolai; Newton, James; Parker, David; Massmind: Binary Division by a Constant Архивная копия от 9 января 2022 на Wayback Machine
- ↑ Vowels, 1992, с. 81–85.
Литература[править | править код]
- R. A. Vowels. Division by 10 // Australian Computer Journal. — 1992. — Т. 24, вып. 3.
- James E. Morris, Krzysztof Iniewski. Nanoelectronic Device Applications Handbook. — CRC Press, 2017. — ISBN 978-1-351-83197-0.
- David L. Harris, Stuart F. Oberman, Mark A. Horowitz. SRT Division: Architectures, Models, and Implementations. — Stanford University, 1998.
- Mark McCann, Nicholas Pippenger. SRT Division Algorithms as Dynamical Systems // SIAM Journal on Computing. — 2005. — Т. 34, вып. 6. — doi:10.1137/S009753970444106X.
- Stuart F. Oberman, Michael J. Flynn. An Analysis of Division Algorithms and Implementations. — Stanford University, 1995.
- Robert E. Goldschmidt. Applications of Division by Convergence. — M.I.T., 1964. — (M.Sc. dissertation).
- Stuart F. Oberman. Floating Point Division and Square Root Algorithms and Implementation in the AMD-K7 Microprocessor // Proceedings of the IEEE Symposium on Computer Arithmetic. — 1999. — С. 106–115. — doi:10.1109/ARITH.1999.762835.
- Peter Soderquist, Miriam Leeser. Division and Square Root: Choosing the Right Implementation // IEEE Micro. — 1997. — July–August (т. 17, вып. 4). — doi:10.1109/40.612224.
- S. F. Anderson, J. G. Earle, R. E. Goldschmidt, D. M. Powers. The IBM 360/370 model 91: floating-point execution unit // IBM Journal of Research and Development. — 1997. — Январь.
- Even Guy, Siedel Peter, Warren Ferguson. A parametric error analysis of Goldschmidt’s division algorithm // Journal of Computer and System Sciences. — 2005. — Февраль (т. 70, вып. 1). — doi:10.1016/j.jcss.2004.08.004.
- Karl Hasselström. Fast Division of Large Integers: A Comparison of Algorithms. — Royal Institute of Technology, 2003. — ((thesis) M.Sc. in Computer Science).
- Christoph Burnikel, Joachim Ziegler. Fast Recursive Division. — Max-Planck-Institut für Informatik, 1998.
- Paul Barrett. Implementing the Rivest Shamir and Adleman public key encryption algorithm on a standard digital signal processor // Proceedings on Advances in cryptology—CRYPTO ’86. — London, UK: Springer-Verlag, 1987. — С. 311–323. — ISBN 0-387-18047-8.
- Torbjörn Granlund, Peter L. Montgomery. Division by Invariant Integers using Multiplication // SIGPLAN Notices. — 1994. — Июнь (т. 29, вып. 6). — doi:10.1145/773473.178249.
- Niels Möller, Torbjörn Granlund. Improved Division by Invariant Integers // IEEE Transactions on Computers. — 2011. — Февраль (т. 60, вып. 2). — doi:10.1109/TC.2010.143.
- Henry S. Warren Jr. Hacker’s Delight. — 2. — Addison Wesley — Pearson Education, Inc., 2013. — ISBN 978-0-321-84268-8.
Литература для дальнейшего чтения[править | править код]
- John J. G. Savard. Advanced Arithmetic Techniques. quadibloc (2018). Дата обращения: 16 июля 2018. Архивировано 3 июля 2018 года.
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Деление натуральных чисел столбиком с остатком
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
Разделим натуральное число 273844 на натуральное число 97.
Проводим деление столбиком и записываем:
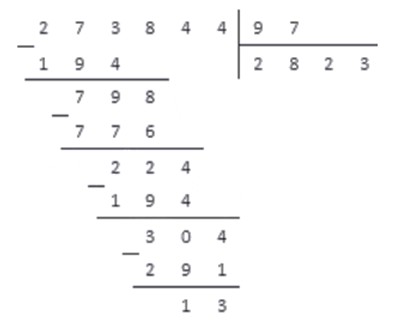
Результат: неполное частное от деления равно 2823, а остаток равен 13.
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3.
Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7-3=4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4-3=1 яблоко.
1 яблоко — это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
7÷3=2 (остаток 1)
Это значит, что число 3 как бы умещается в числе 7 два раза, а единица — остаток, меньший чем 3.
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Вычислим: 145÷46.
145-46=99.
Число 99 больше, чем 46, поэтому продолжаем последовательное вычитание делителя:
99-46=53.
Повторяем эту операцию еще раз:
53-46=7
В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток — результат вычитания, который меньше делителя. В нашем случае остатком является число 7.
145÷46=3 (остаток 7).
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если a<b, то a÷b=0 (остаток a).
Например:
12÷36=0 (остаток 12)47÷88=0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1, 2, 3 и т.д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d=a-b·c. Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0, 1, 2, 3 и т.д. Применяя формулу d=a-b·c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b. Число, взятое за с на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Разделим 267 на 21.
a=267; b=21. Подберем неполное частное.
Используем формулу d=a-b·c и будем последовательно перебирать c, придавая ему значения 0, 1, 2, 3 и т.д.
Если с=0, имеем: d=a-b·c=267-21·0=267. Число 267 больше, чем 21, поэтому продолжаем подстановку.
При с=1 имеем: d=a-b·c=267-21·1=246. Т.к. 246>21, снова повторяем процесс.
При с=2 имеем: d=a-b·c=267-21·2=267-42=225; 225>21.
При с=3 имеем: d=a-b·c=267-21·3=267-63=204; 204>21.
…
При с=12 имеем: d=a-b·c=267-21·12=267-252=15;15<21.
На этом этапе процесс деления можно считать законченным. Неполное частное с=12, а остаток деления равен 15.
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Вспомним, что в случае, когда a<b, неполное частное равно нулю, а остаток равен делимомому a. Мы будем рассматривать случай, когда a>b.
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: a и b.
Найти нужно неполное частное c и остаток d.
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a=b·c+d. Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a=b·c+d, тогда мы найдем искомые величины.
Алгоритм деления, благодаря которому мы представим a в виде суммы a=b·c+d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47.
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе — два.
3-2=1
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем примере справа от 47 дописываем нуль. Так как 470<899, запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.
3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10. В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на 1, 2, 3.. и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере — десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470.
470<899, поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47·20=940; 940>899.
Число, которое мы получили на предпоследнем шаге (470=47·10) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги 1-5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1-5, но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. 899-470=429, 429>47. Повторяем шаги 1-5 алгоритма с числом 429, взятым в качестве делимого.
1. В записи числа 429 на один знак больше, чем в записи числа 47. Запоминаем разницу — число 1.
2. В записи делимого справа дописываем один нуль. Получаем число 470. Так как 470>429, из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1-1=0. Запоминаем 0.
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель 47 на 1, 2, 3 .. и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47·9=423<429, 47·10=470>429. Таким образом, второе искомое слагаемое — 47·9=423.
5. Разность между 429 и 423 равна числу 6. Так как 6<47, это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899=470+423+6. Вспоминаем, что 470=47·10, 423=47·9. Перепишем равенство:
899=47·10+47·9+6
Применим распределительное свойство умножения.
899=47·10+47·9+6=47·(10+9)+6
899=47·19+6.
Таким образом, мы представили делимое в виде уже данной ранее формулы a=b·c+d.
Искомые неизвестные:неполное частное с=19, остаток d=6.
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Разделим числа 42252 и 68.
Используем алгоритм. Первые пять шагов дают первое слагаемое — число 40800=68·600.
Снова повторяем первые пять шагов алгоритма с числом 1452=42252-40800 и получаем второе слагаемое 1360=68·20
Третий раз проходим шаги аглоритма, но у же с новым числом 92=1452-1360. Третье слагаемое равно 68=68·1. Остаток равен 24=92-68.
В результате получаем:
42252=40800+1360+68+24=68·600+68·20+68·1+24==68·(600+20+1)+24=68·621+24
Неполное частное равно 621, остаток равен 24.
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства a=b·c+d. Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Проверим, верно ли, что 506÷28=17 (остаток 30).
Сравниваем остаток и делитель: 30>28.
Значит, деление выполнено неверно.
Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5. Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: 5<13.
Первый пункт проверки пройден, переходим ко второму.
Запишем формулу a=b·c+d. a=121; b=13; c=9; d=5.
Подставляем значения и сравниваем результаты
13·9+5=117+5=122; 121≠122
Значит, в вычисления школьника где-то закралась ошибка.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111. В результате у него получилось число 54 с остатком 4. Все ли правильно посчитано?
Проверим! Остаток 4 меньше, чем делитель 111, поэтому переходим ко второму этапу проверки.
Используем формулу a=b·c+d, где a=5998; b=111; c=54; d=4.
После подстановки, имеем:
5998=111·54+4=5994+4=5998.
Равенство корректно, а значит, и деление выполнено верно.
Федор Комов
Ученик
(195)
8 лет назад
Вот пример:
int main()
{
int k,e;
std::cin >> k;
e=k%10;
std::cout << e;
system(«pause»);
return 0;
}
Вводишь к примеру число 12
12%10=2
Если целочисленное деление :
12/10=1
Globe
Просветленный
(24825)
8 лет назад
Алгоритм примерно такой. Пусть надо найти остаток от деления 26 на 5.
1) Переходим в двоичную систему счисления. Получаем 26=11010 и 5=101.
2) Как видим, делимое имеет пять значащих разрядов, а делитель — три. Сдвинем делитель на 5-3=2 разряда, получим 10100. Это число меньше 11010. Вычтем: 11010-10100= 110
3) остаток из п. 2 имеет то же число значащих разрядов и больше делителя. Вычтем: 110-101=1
4) Получили остаток 1. Это и есть ответ.
То есть, деление сводится к двоичным сдвигам и вычитаниям.
Автор: Виктор Трофимов, МОУ гимназия №5, г. Волгодонск, Ростовская обл.
В Паскале существует возможность использования трех методов определения кратности числа.
1. С помощью оператора div (целоисчисленное деление). Как это работает?
x := 10 div 2 (переменная x получит значение 5; процессор вычисляет пример 10 / 2 и выдает результат 5)
x := 10 div 3 (переменная x получит значение 3; вычисляется 10 / 3 = 3,33 и отбрасывается дробная часть, такова природа работы оператора div)
x := 10 div 4 (переменная x получит значение 2; 10 / 4 = 2,5 – и опять отбрасывается дробная часть).
2. С помощью оператора mod (остаток от деления).
Тут и понятно, остаток от деления числа, которое полностью делится на делитель, будет равен нулю.
x := 10 mod 2 (переменная x получит значение 0; процессор вычисляет по формуле 10 – ((10 div 2) * 2) = 0, то есть оператор mod возвращает пользователю остаток, который получится в результаты вычитания из делимого числа разницы между первым в сторону уменьшения делящимся нацело на делитель… эмм, надеюсь, понятно. Еще на примерах:
x := 10 mod 3 (переменная x получит значение 1; происходит следующее 10 div 3 = 3 (целое), дальше 10 – 3 (результат) * 3 (делитель) = 1)
x := 10 mod 4 (переменная x получит значение 2; вычисляется 10 – ((10 div 4) * 4)).
Внимательно изучите работу операторов div и mod, они важны для решения задач ГИА по информатике.
3. С помощью функции отбрасывания дробной части числа (не округления, а именно отбрасывания).
trunc(z), где z – вещественное число или математическое выражение.
Примеры:
x := trunc(3.33) (x получит значение 3; «удаляется» дробная часть)
x := trunc(10 / 3) (x получит значение 3, 10 / 3 = 3.33, отбрасываем «,33»)
x := trunc(10 / 2) (x получит значение 5, 10 / 2 = 5 (целое число))
x := trunc(10 / 4) (x получит значение 2, 10 / 4 = 2.5, отбрасываем дробную часть)
Но этот метод не совсем удобен, так как дублирует более понятный в тексте программы div. Таким же образом можно проверить кратность чисел:
Если ((x mod 3) = 0), то число кратно трем (остаток от деления равен нулю).
Если ((x mod  = 0), то число кратно восьми и т.д.
= 0), то число кратно восьми и т.д.
Как найти цифру, на которую оканчивается число? Все просто, надо найти остаток от деления числа на 10.
Примеры:
Результатом 150 mod 10 будет число 0, т.к. 150 полностью делится на 10. 0 – это последняя цифра числа.
153 mod 10 вернет 3 (153 – ((153 div 10) * 10); 3 – эта цифра, на которую оканчивается число.
87 mod 10 вернет 7 – последнюю цифру числа.
33 mod 10 вернет 3 и т.д. Попробуйте сами: writeln(33 mod 10);
Автор:
















